За последнее время у меня набралось определённое количество заметок на различные темы, с которыми до конца не ясно что делать. Скорее всего, для синих эта информация не слишком актуальна, для красных — давно очевидна. Из этих заметок вряд ли получится сделать статьи, а достаточно заинтересованный человек вполне может собрать всю приведённую в них информацию из интернета по частям самостоятельно. Тем не менее, я всё же решил сделать пост (или, может быть несколько) на Codeforces, в надежде, что эти сведения для кого-нибудь окажутся полезными.
Оригинальная задача KQUERY формулируется следующим образом. Дан массив  размера
размера 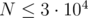 , а также
, а также 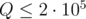 запросов вида
запросов вида 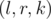 — определить количество элементов, больших
— определить количество элементов, больших 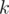 , на отрезке
, на отрезке 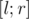 .
.
Сразу следует заметить, что из-за достаточно малого TL вердикт Accepted по оригинальной задаче получает только одно из приведённых ниже решений. Тем не менее, рассмотрение альтернативных подходов к задаче также не лишено смысла.
Online-версия задачи KQUERY — KQUERYO. Среди её особенностей — увеличенный TL и некорректные тесты (см. комментарии к задаче). Все показанные online-решения получают применительно к данной задаче вердикт Accepted.
Dynamic-версия задачи KQUERY — KQUERY2. В данном посте эта задача (пока) не рассматривается; её обсуждение можно найти здесь.
Решение #1: merge tree
Препроцессинг 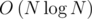 , ответ на запрос
, ответ на запрос 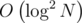 , online
, online
Создадим дерево отрезков, у которого в вершине, соответствующей подотрезку 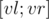 , хранится отсортированный вектор элементов массива
, хранится отсортированный вектор элементов массива 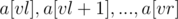 (в иностранных источниках такое дерево отрезков иногда называют merge tree). Объединять отсортированные вектора можно при помощи алгоритма STL merge().
(в иностранных источниках такое дерево отрезков иногда называют merge tree). Объединять отсортированные вектора можно при помощи алгоритма STL merge().
При обработке запроса к отрезку 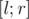 мы, как обычно, спускаемся к вершинам, подотрезки которых входят в целевой отрезок, и в каждой из этих вершин выполняем двоичный поиск, чтобы определить количество элементов, больших
мы, как обычно, спускаемся к вершинам, подотрезки которых входят в целевой отрезок, и в каждой из этих вершин выполняем двоичный поиск, чтобы определить количество элементов, больших 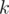 .
.
Решение #1a: частичное каскадирование
Препроцессинг 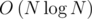 , ответ на запрос
, ответ на запрос 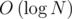 , online
, online
В предыдущем решении мы использовали двоичный поиск, чтобы в каждой вершине, подотрезок которой входит в отрезок запроса, находить индекс первого элемента, большего 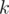 . Мы могли бы определять этот индекс за
. Мы могли бы определять этот индекс за 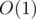 , если бы в каждой вершине была сохранена дополнительная информация.
, если бы в каждой вершине была сохранена дополнительная информация.
Пусть 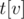 — отсортированный вектор, хранящийся в вершине
— отсортированный вектор, хранящийся в вершине  ,
, 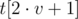 и
и 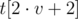 — отсортированные вектора, хранящиеся в её левом и правом потомках. Пусть в вершине
— отсортированные вектора, хранящиеся в её левом и правом потомках. Пусть в вершине  также имеются массивы
также имеются массивы 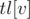 и
и 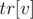 , такие что
, такие что 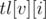 — индекс первого элемента, большего или равного
— индекс первого элемента, большего или равного 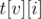 , в массиве
, в массиве 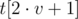 ,
, 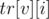 — аналогичный индекс в массиве
— аналогичный индекс в массиве 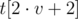 . Тогда, зная индекс
. Тогда, зная индекс  первого элемента, большего
первого элемента, большего 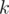 , в массиве вершины
, в массиве вершины  , мы за
, мы за 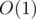 определяем индекс первого элемента, большего
определяем индекс первого элемента, большего 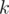 , в массивах вершин-потомков (это
, в массивах вершин-потомков (это 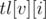 и
и 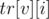 ).
).
Массивы 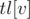 и
и 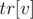 формируются в функции build(), когда выполняется объединение двух отсортированных массивов в один. Можно выполнять это объединение вручную, как в сортировке слиянием, попутно заполняя массивы
формируются в функции build(), когда выполняется объединение двух отсортированных массивов в один. Можно выполнять это объединение вручную, как в сортировке слиянием, попутно заполняя массивы 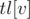 и
и 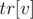 .
.
При обработке запроса достаточно выполнить бинпоиск в корневой вершине, чтобы найти индекс первого элемента, большего 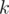 , а далее обновлять его значениями из
, а далее обновлять его значениями из 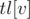 и
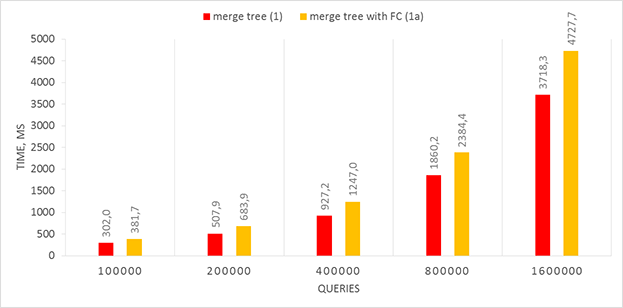
и 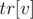 . Данную технику называют частичным каскадированием (fractional cascading), она позволяет снять лишний логарифм при обработке запросов.
. Данную технику называют частичным каскадированием (fractional cascading), она позволяет снять лишний логарифм при обработке запросов.
Практика, однако, показывает, что несмотря на лучшую асимптотическую оценку, данное решение работает на 30-40% медленнее предыдущего, поэтому пользоваться им не стоит.
Решение #2: сканирующая прямая по значениям (ординатам)
Препроцессинг 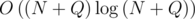 , ответ на запрос
, ответ на запрос 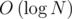 , offline
, offline
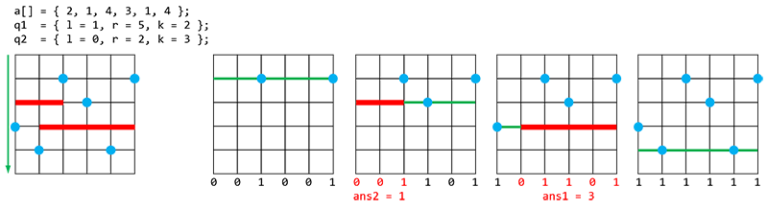
Рассмотрим геометрическую интерпретацию исходной задачи. Если элементы массива  представить на плоскости в виде точек
представить на плоскости в виде точек 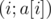 , то ответом на запрос
, то ответом на запрос 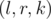 является количество точек, лежащих выше отрезка
является количество точек, лежащих выше отрезка 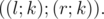
Введём два вида событий: появление точки и появление запроса. Отсортируем все события в порядке убывания ординат (для точек это 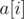 , для запросов —
, для запросов — 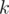 ). По абсциссам построим стандартное дерево отрезков для суммы, в котором будем отмечать появление точек.
). По абсциссам построим стандартное дерево отрезков для суммы, в котором будем отмечать появление точек.
При обработке появления точки присваиваем в дереве отрезков единицу её абсциссе  . При обработке появления запроса определяем сумму на отрезке
. При обработке появления запроса определяем сумму на отрезке 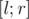 . Заметим, что если разные события имеют одинаковую ординату, в первую очередь должны обрабатываться события, связанные с запросами.
. Заметим, что если разные события имеют одинаковую ординату, в первую очередь должны обрабатываться события, связанные с запросами.
Решение #3: сканирующая прямая по индексам (абсциссам)
Препроцессинг 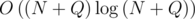 , ответ на запрос
, ответ на запрос 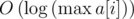 , offline
, offline
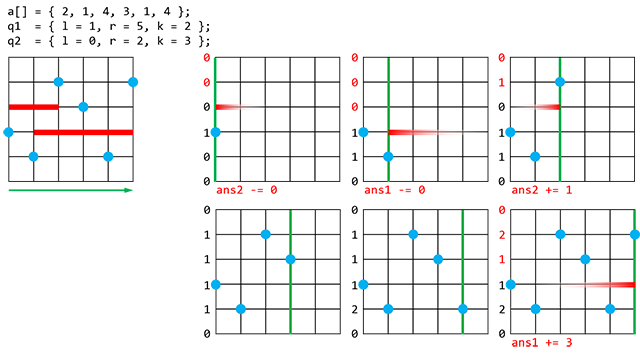
Продолжим использовать ту же геометрическую интерпретацию задачи, что и для предыдущего решения, но теперь сканирующая прямая движется не сверху вниз, а слева направо.
Введём три вида событий: появление точки, начало запроса, конец запроса. Отсортируем все события в порядке возрастания абсцисс (для точек это  , для начал запросов —
, для начал запросов —  , для концов запросов —
, для концов запросов —  ). По ординатам построим стандартное дерево отрезков для суммы, в котором будем отмечать появление точек.
). По ординатам построим стандартное дерево отрезков для суммы, в котором будем отмечать появление точек.
При обработке появления точки присваиваем в дереве отрезков единицу её ординате 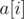 . При обработке начала запроса вычитаем из ответа сумму на отрезке
. При обработке начала запроса вычитаем из ответа сумму на отрезке 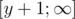 , при обработке конца запроса добавляем к ответу сумму на отрезке
, при обработке конца запроса добавляем к ответу сумму на отрезке 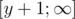 . Если разные события имеют одинаковую абсциссу, сначала обрабатываются начала запросов, затем точки, затем концы запросов.
. Если разные события имеют одинаковую абсциссу, сначала обрабатываются начала запросов, затем точки, затем концы запросов.
Решение #3a: неявное дерево отрезков
Препроцессинг 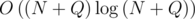 , ответ на запрос
, ответ на запрос 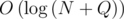 , offline
, offline
Используем сжатие координат или неявное дерево отрезков, чтобы снизить потребление памяти с 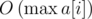 до
до 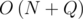 . Время обработки запроса при этом сократится от
. Время обработки запроса при этом сократится от 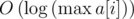 до
до 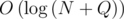 .
.
Неявное дерево отрезков строится не в массиве, а полностью на указателях. Новые вершины создаются только в том случае, если к ним обращается функция модификации дерева.
Решение #3b: персистентное дерево отрезков
Препроцессинг 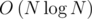 , ответ на запрос
, ответ на запрос 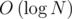 , online
, online
Оставим в геометрической интерпретации только точки и сохраним версии неявного дерева отрезков для каждого индекса  . Каждая новая версия не дублирует все вершины предыдущей, а добавляет только
. Каждая новая версия не дублирует все вершины предыдущей, а добавляет только 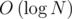 изменённых вершин.
изменённых вершин.
Для ответа на запрос 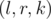 требуется вычислить сумму на отрезке
требуется вычислить сумму на отрезке 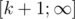 в версии
в версии  и вычесть сумму на отрезке
и вычесть сумму на отрезке 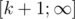 в версии
в версии  .
.
Решение #4: sqrt-декомпозиция
Препроцессинг 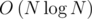 , ответ на запрос
, ответ на запрос 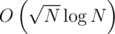 , online
, online
Разделим исходный массив на блоки размером 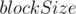 (получится
(получится 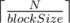 блоков). Отсортируем каждый из блоков.
блоков). Отсортируем каждый из блоков.
Пусть выполняется запрос к отрезку 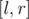 . В тех блоках, которые полностью покрываются отрезком запроса, количество чисел, больших
. В тех блоках, которые полностью покрываются отрезком запроса, количество чисел, больших 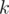 , может быть найдено двоичным поиском. На концах отрезка
, может быть найдено двоичным поиском. На концах отрезка 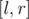 , не покрывающих полностью соответствующие блоки (а также в том случае, когда
, не покрывающих полностью соответствующие блоки (а также в том случае, когда  и
и  принадлежат одному блоку), ответ считается наивным методом за линейное время. Таким образом, время ответа на запрос выражается как
принадлежат одному блоку), ответ считается наивным методом за линейное время. Таким образом, время ответа на запрос выражается как 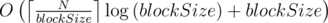 .
.
При 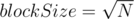 получаем классическую sqrt-декомпозицию, имеющую время обработки запроса
получаем классическую sqrt-декомпозицию, имеющую время обработки запроса 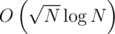 . Можно попытаться улучшить это значение, подобрав размер
. Можно попытаться улучшить это значение, подобрав размер 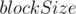 так, чтобы минимизировать выражение
так, чтобы минимизировать выражение 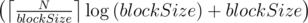 . При
. При 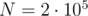 таким значением будет
таким значением будет 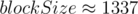 . Тем не менее, фактическое увеличение производительности по сравнению с sqrt-декомпозицией составляет ~5%, что влечёт общую нецелесообразность подобной оптимизации.
. Тем не менее, фактическое увеличение производительности по сравнению с sqrt-декомпозицией составляет ~5%, что влечёт общую нецелесообразность подобной оптимизации.
Сравнение быстродействия решений
Сформируем массив  размера
размера 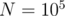 , заполненный случайными числами из диапазона
, заполненный случайными числами из диапазона 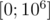 . Затем выполним
. Затем выполним 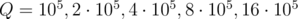 случайных KQUERY-запросов к данному массиву. Для каждого значения
случайных KQUERY-запросов к данному массиву. Для каждого значения 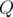 произведём 10 тестов, в качестве итогового времени возьмём среднее.
произведём 10 тестов, в качестве итогового времени возьмём среднее.
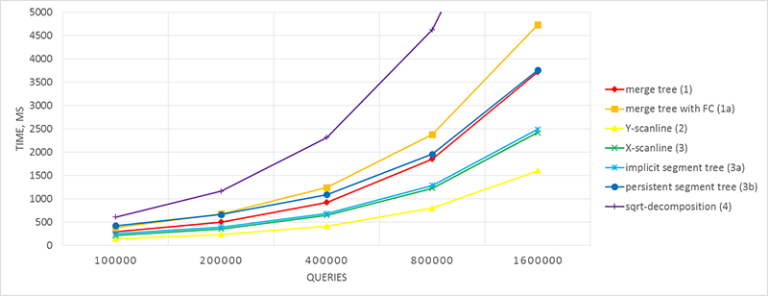
Можно видеть, что наиболее быстрым из online-решений является использование дерева отрезков с отсортированными подмассивами в вершинах, имеющее асимптотику 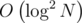 на запрос (!).
на запрос (!).
Как было упомянуто ранее, в оригинальной задаче KQUERY вердикт Accepted получает только offline-решение #2 (сканирующая прямая по убыванию ординат). Можно попробовать произвести (неасимптотические) оптимизации других решений: не использовать ООП-стиль, заменить std::vector на статические массивы и т. д. Описание оптимизаций, достойных внимания, приветствуется в комментариях.
Другие задачи, сводящиеся к KQUERY
Количество различных чисел на отрезке (DQUERY)
Существует простое сведение задачи DQUERY к задаче KQUERY за время 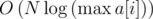 .
.
Определим массив 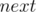 , такой что
, такой что 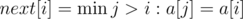 . Другими словами,
. Другими словами,  -й элемент массива
-й элемент массива 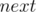 содержит индекс следующего справа элемента, равного
содержит индекс следующего справа элемента, равного 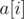 (если
(если 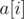 — последнее появление элемента, то
— последнее появление элемента, то 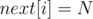 ).
).
Количество различных элементов на отрезке — это количество элементов, справа от которых на отрезке нет равных им, то есть количество таких 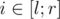 , что
, что 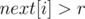 . Таким образом, результат запроса DQUERY
. Таким образом, результат запроса DQUERY 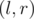 к массиву
к массиву  равен результату запроса KQUERY
равен результату запроса KQUERY 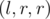 к массиву
к массиву 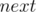 .
.
На spoj.com задачу DQUERY можно сдать с использованием любого из показанных выше решений, кроме самого медленного (#4, sqrt-декомпозиция).
Обсуждение задачи на Codeforces
K-я порядковая статистика на отрезке (MKTHNUM)
Используя бинарный поиск по ответу, любое online-решение задачи KQUERY можно преобразовать в решение задачи MKTHNUM, асимптотика которого будет в 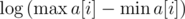 раз выше: из решений KQUERY с асимптотикой
раз выше: из решений KQUERY с асимптотикой 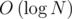 и
и 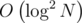 получаются решения MKTHNUM с асимптотикой
получаются решения MKTHNUM с асимптотикой 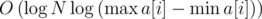
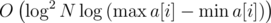 соответственно.
соответственно.
На spoj.com задачу MKTHNUM можно сдать с использованием любого из online-решений, кроме самого медленного (#4, sqrt-декомпозиция). В решении #3b нужно аккуратно учитывать отрицательные элементы массива.
Важно, что эта задача имеет online-решение с временем обработки запроса 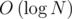 . Это решение (не рассматриваемое здесь подробно) получается из решения #3b, но вместо бинарного поиска по ответу используется параллельный спуск по деревьям отрезков версий
. Это решение (не рассматриваемое здесь подробно) получается из решения #3b, но вместо бинарного поиска по ответу используется параллельный спуск по деревьям отрезков версий  и
и  .
.
Обсуждение задачи на Codeforces
Решения указанных задач также приведены в лекции ЗКШ 2015 (автор Burunduk1).











Существует еще решение этой задачи, при помощи алгоритма МО, например, алгоритмом МО можно загнать в ТЛ задачу DQUERY: код
Решение с корневой можно ускорить (АССИМПТОТИЧЕСКИ). Пусть мы разбили на A блоков. Тогда на запрос мы будем тратить O(N * logN / A + A). Баланс этих двух слагаемых — это когда они равны : N logN / A = A, то есть A = sqrt(NlogN). Ассимптотика улучшилась до O(N*sqrt(NlogN)).
Еще можно за O(N*sqrt(N)) алгоритмом МО (оффлайн, разновидность корневой), о котором речь в предыдущем комментарии. Постараюсь разъяснить идею подробнее : разобъем запросы на группы. Каждому запросу [l; r] будет соответствовать группа с номером l / sqrt(N). То есть это номер блока длины sqrt(N), в который попадет левая граница запроса. Для каждой группы решим задачу независимо: 1. Отсортируем запросы внутри группы по правой границе (не учитывая левые никак) 2. Будем идти двумя указателями l1 и r1 и поддерживать S — ответ внутри отрезка [l1;r1]. Изначально l1 и r1 установлены в самом начале блока. Пройдемся по всем запросам. r1 будем двигать "направо" на 1 позицию, пока не достигнем r[i] — правой границы i-го запроса в блоке. При переходе от отрезка [l1; r1] к [l1; r1 + 1] нужно к S добавить 1, если a[r1 + 1] > k, а иначе — оставить S прежним. Итак, теперь одна проблема : индекс r1 уже достиг позиции конца текущего запроса. А вот l1 стоит либо в начале (если текущий запрос — самый первый), либо в позиции l[i — 1] — левой границе предыдущего запроса. Будем двигать l1 до l[i] (неизвестно — направо или налево, l[i] не отсортированы внутри блока). Если l1 придется двигать налево, то будем проверять, что a[l1] > k и добавлять 1 к S, если ДА. А если l1 двиграется налево, то в случае a[l1] > k, нужно будет отнять от S единицу, т.к. a[l1] раньше было в нашем отрезке, а теперь уже нет.
Докажем ассимптотику : пусть в i-й группе находится cnt[i] запросов. Тогда Заметим, что указаьтель r1 двигается только направо, а значит суммарно он пройдет максимум n позиций. А вот указатель l1 при переходе к следующему запросу может в худшем случае "пробежать" весь блок длины sqrt(N) (если он был в начале блока, а левая граница след. запроса — в конце). То есть суммарно на i-ю группу мы потратили O(cnt[i] * sqrt(N) + N) в худшем случае. Просуммируем это по всем i = 0..sqrt(N). Первое слагаемое превратится в sqrt(N) * sum(cnt[i]) = sqrt(N) * N, т.к. всего запросов N. А второе слагаемое превратится N * sqrt(N), т.к. групп sqrt(N). Значит решение отработает O(N * sqrt(N)). На практике это очень быстрое решение с хорошей константой, в отличае от дерева отрезков, т.к. все операции быстрые и нет никакой рекурсии, и на самом деле "худшие случаи", о которых шла речь в доказательстве ассимптотики редко достигаются. Так что это решение может оказаться быстрее остальных
UPD : я алгоритмом МО решил немного другую задачу, где k = const для всех запросов. Чтобы превратить мое решение в решение исходной задачи, нужно хранить, например, дерево Фенвика (оно достаточно быстрое) на сумму и при добавлении a[i] в отрезок [l1;r1] прибавлять 1 в точке a[i] в дереве Фенвика, а при удалении — отнимать. Ответ на запрос — это кол-во чисел > k, то есть текущая сумма на отрезке [k; +inf]. Такое решение отработает за O(N * sqrt(NlogN)), если сделать блоки длиной sqrt(N / logN), но константа будет очень хорошая
О а еще можно сжимать координаты и тогда решение такое же как неявным деревом отрезков только ответ на запрос за log N.