How to solve problem B ?
This problem looks similar to SPOJ-WATER
Someone please explain the approach to this problem?
Thank you!
→ Обратите внимание
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 3993 |
| 2 | jiangly | 3743 |
| 3 | orzdevinwang | 3707 |
| 4 | Radewoosh | 3627 |
| 5 | jqdai0815 | 3620 |
| 6 | Benq | 3564 |
| 7 | Kevin114514 | 3443 |
| 8 | ksun48 | 3434 |
| 9 | Rewinding | 3397 |
| 10 | Um_nik | 3396 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
→ Найти пользователя
→ Прямой эфир
↑
↓
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 23.11.2024 21:54:30 (j2).
Десктопная версия, переключиться на мобильную.
При поддержке
Списки пользователей


| Название |
|---|











I approached it in a way similar to Bellman Ford Algorithm . Take a matrix W and fill all the entries with infinity except the ones present in the border of the grid ie. i = 0 || i = (R - 1) || j = 0 || j = (C - 1) where i, j are the row index and column index respectively.
Now for each cell in the interior of the matrix water can come from 4 adjacent cells . We need to find the minimum of the incoming water from these cells and make this the new W[i][j] only if its greater than H[i][j]
For each cell with index i, j: min = min(W[x][y])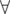 x, y adjacent to i, j and W[i][j] = max(min, H[i][j])
x, y adjacent to i, j and W[i][j] = max(min, H[i][j])
You need to run this relaxation for R * C times
My Java Code:
Link