Соревнование Codeforces Marathon Round 1 закончено (комментарий с результатами). Пока тестируются итоговые решения, думаю, многим участникам будет интересно поделиться своими идеями и узнать альтернативные подходы. Начну с идей, которые испробовал я — и успешных, и нет; по коду посылок видно, что у участников интересных идей больше, но, надеюсь, они сами их расскажут. У каждого решения ниже в квадратных скобках указаны минимальный, средний и максимальный баллы при тестировании на 1000 локальных тестов. Замечу сразу, что константы и технические детали в решениях не претендуют на оптимальность: баллы лишь отражают примерное соотношение идей и часто могут быть чуть улучшены. -----
Решение 1 [4099 4159.699 4288]: случайное.
Просто выведем 100 раз 5000 случайных битов.
Решение 2 [4160 4226.294 4365]: запоминание последнего бита.
Последний проверенный бит всегда неправильный. Например, если ответ на попытку — число 4050, значит, ровно на 4050-м бите нашей строки случилась 2000-я ошибка. Зафиксируем правильное значение этого бита. При генерации очередной случайной строки все зафиксированные биты имеют уже известные нам значения, остальные генерируются случайно.
Решение 3 [4182 4291.374 4453]: выяснение нескольких битов.
Это решение из двух частей. В первой части (90 попыток) попытки разделены на 45 пар. Первая попытка пары i генерируется случайно (кроме зафиксированных битов, которые нам уже известны). Вторая попытка пары i отличается только в i-м бите и в последнем проверенном бите.
Какую информацию мы можем получить из такой пары? Пусть, например, первая попытка дала результат 3980, а вторая (в ней поменялись бит 1 и бит 3980) — результат 3975. Значит, во-первых, бит 1 был правильным в первой попытке (раз она прошла дальше). Во-вторых, 2000-я ошибка во второй попытке — это 1999-я ошибка в первой, а значит, между 3975 и 3980 битами в наших попытках нет ни одной ошибки.
Аналогично, если результат второй попытки больше первой — например, 3981, - мы знаем, что бит 1 был правильным во второй попытке, а ещё что между 3980 и 3981 ошибок нет (в этот раз это нам ничем не помогло, потому что и битов между ними нет).
За пару попыток мы точно узнаём в среднем три бита.
Во второй части решения (оставшиеся 10 попыток) будем просто генерировать случайные строки, кроме зафиксированных битов, которых в среднем получилось 135 и становится на один больше после каждой попытки.
Решение 4 [4260 4369.927 4498]: симметричное выяснение нескольких битов.
Это решение из двух частей. В первой части (90 попыток) первая попытка делается случайно, а каждая следующая (i-я) меняет бит i и последний проверенный бит в предыдущей. Как и в решении 3, по тому, как изменился ответ, мы можем не только понять на будущее, каким должен быть бит i, но и узнать в среднем два бита в районе 4000. Однако теперь мы узнаём в среднем три бита за одну попытку, а не за пару. Заметим, что мы не можем выставлять первые 89 битов в правильные значения сразу, поэтому известные в конце биты распределены более симметрично вокруг 4000.
Во второй части решения (оставшиеся 10 попыток) будем просто генерировать случайные строки, кроме зафиксированных битов, которых в среднем получилось 267 и становится на один больше после каждой попытки.
На этом решения, выясняющие конкретные биты, у меня закончились. Судя по предварительной таблице, больше половины участников придумали кое-что получше. Полезная эвристика отсюда, которая может помочь в других решениях - всегда запоминать, что последний проверенный бит точно неправильный.
Решение 5 [4429 4533.129 4671]: инвертирование отрезков.
Разобъём наши 5000 битов на отрезки длины, например, 45. Для первой попытки сгенерируем случайную строку, а в каждой следующей попытке будем инвертировать очередной отрезок. После инвертирования мы, сравнив два числа, точно знаем, лучше было с инвертированием или без него; выберем наилучшее из двух положений и перейдём к следующей попытке.
Почему это вообще работает? Интуитивно — среднее отклонение на отрезке достаточно большое, значит, будет достаточно много отрезков, на которых инвертирование сильно меняет ответ: например, если на отрезке было 19 из 45 правильных битов, после инвертирования их становится 26. Если мы, наоборот, из 26 сделали 19 — вернём 26 (и предыдущий результат) на место.
Константа 45 подбиралась на глаз; кажется, большинству участников в каких-то похожих решениях больше понравилась константа 40.
Решение 6 [4399 4582.368 4723]: инвертирование отрезков с возобновлением.
Положим 4000 первых позиций битов в пул "настоящее", а оставшиеся 1000 позиций в пул "будущее". Для первой попытки, как обычно, сгенерируем случайную строку. Для каждой следующей попытки возьмём из пула "настоящее" 79 случайных битов и инвертируем их все. Если ответ изменился больше чем на 10 — значит, на этом "отрезке" есть достаточно большое отклонение. Воспользуемся этим: зафиксируем все эти 79 битов в лучшем из двух состояний (либо все оставим, либо все инвертируем обратно). В противном случае также выставим лучшее из двух состояний, но фиксировать биты не будем, а переложим их в пул "будущее".
Когда пул "настоящее" кончился, возьмём из пула "будущее" все биты, до которых мы хоть раз дошли (то есть бит 4999, скорее всего, не берём), сделаем из них новое "настоящее" и продолжим.
За счёт того, что мы переиспользуем биты, фиксирование которых не приносит большой выгоды, мы можем брать более длинные "отрезки": их длина 79 вместо 45 в решении 5. А значит, и среднее отклонение на "отрезках" будет больше.
Константы 79 и 10 подбирались небольшим перебором.
Решение 7 [4539 4702.079 4878]: инвертирование отрезков с возобновлением и запоминанием.
Будем делать то же, что в решении 6, но вспомним про идею из предыдущей серии решений: последний проверенный бит всегда неправильный. Выгода от применения этой идеи почти не зависит от выгоды от инвертирования больших отрезков.
В этой версии решения оказалось выгодно сделать отрезок ещё длиннее: константы 79 и 10 заменены на 99 и 18.
Решения с инвертированием отрезков на этом кончаются. Лучшее из них в предварительной таблице занимает 20-30 место. Слабые стороны этих решений в том, что мы меняем только малую часть строки, а значит, получаем в среднем мало битов информации. Ещё мы фиксируем раз и навсегда весь хороший отрезок. Что из этого и как можно улучшить — надеюсь, расскажут участники из топа.
Решение 8 [4251 4403.645 4594]: дискретное вероятностное в каждой позиции.
Сделаем 99 случайных попыток. Для каждой из 5000 позиций будем запоминать вероятные биты. Для каждой попытки с результатом хотя бы 4000 отметим её биты до последнего проверенного как вероятные на всех позициях, а для каждой попытки с результатом меньше 4000 — инвертируем её и отметим инвертированные биты до последнего проверенного как вероятные.
В последней попытке в каждой позиции выберем тот вариант, который больше раз оказался вероятным.
Решение 9 [4433 4601.678 4773]: вероятностное в каждой позиции с запоминанием.
Попробуем улучшить предыдущее решение.
Во-первых, вспомним про то, что последний проверенный бит всегда неправильный, и будем фиксировать такие биты.
Во-вторых, научимся использовать не только знак результата (условно — меньше ли он 4000), но и величину. Например, если 2000 ошибок как-то распределены по 4001 биту, это нужно учитывать с меньшим коэффициентом, чем когда те же 2000 ошибок распределены по 4100 битам.
С учётом зафиксированных битов каждая попытка даёт нам информацию вида "в t битах 1999 ошибок". В каждом из этих t битов запишем, что вероятность того, что он правильный, равна 1999 / t. В конце просто усредним все записи в каждом бите.
В последней попытке в каждой позиции выберем тот вариант, который оказался более вероятным.
Около трети участников реализовали что-то лучше, чем описанные решения, считающие вероятности отдельно в каждой позиции.
Ещё одна идея — полное инвертирование. Будем использовать попытки парами, вторая попытка пары — полная побитовая инверсия первой. Каждая такая пара попыток даёт информацию вида "на отрезке от lo до hi ровно err ошибок". Действительно, пусть первая попытка пары дала результат 4015, а вторая 3980. В сумме на отрезках [1, 3980] и [1, 4015] 4000 ошибок. Кроме того, в сумме от 1 до 3980 ровно 3980 ошибок: каждый бит побывал и нулём, и единицей ровно по одному разу. Значит, среди битов от 3981 до 4015 ошибок ровно 20.
С этими отрезками можно делать разные операции: пересекать их, искать строку, подходящую под всю известную информацию, если не получается — искать как можно лучше подходящую строку. Мои решения с такими отрезками получают средние результаты между 4400 и 4500, но уже технически нагружены. Наверняка можно сделать лучше.
Немного об истории задачи. Изначально она задумывалась как сложная неточная задача на соревнование по правилам ACM ICPC. План был такой: испробовать несколько подходов и посмотреть, отсекаются ли ограничениями простые и слабые от содержательных и сильных. Однако первые же несколько идей решения не пожелали выстроиться по результату в порядке, сколько-нибудь похожем на сложность их реализации, так что задачу пришлось отложить. С другой стороны, в соревнование с частичной оценкой такая задача хорошо вписывается, поскольку есть несколько совсем разных идей решения, придумать и реализовать которые достаточно легко.
Напоследок хочу поблагодарить Наталью Гинзбург (naagi), Андрея Лопатина (KOTEHOK) и Михаила Мирзаянова (MikeMirzayanov) за помощь в подготовке и проведении соревнования.
So, I'd like to share my approach (1st place before systests so far).
The first thing to do for me was to implement evaluator. Input strings are random (there are no patterns in tests to my knowledge), so the scores are fully reproducible locally. So I don't get why many of participants (even in top-10) have lots of submits with scores going up/down randomly — am I missing something?
I tried to estimate the best possible score from information counting reasoning. Assuming we're getting responses in range 0-5k, it is 12-13 bits per response, 1200-1300 bits for the whole session, which seems enough (we need to get 1k bits of information to win). However, any sane approach I could think of would be getting responses in range 4k-5k, so it is less than 10 bits per response, so this is really tight. With this reasoning, I was surprised to see such high scores in scoreboard, but nevertheless decided to try to solve the problem.
My first idea wase to try some greedy/hill climbing approaches. Unfortunately local evaluation was showing scores around 300. Maybe with some careful tuning it can produce better results, but I didn't want to spend my time on tuning. So I decided to abandon this direction and use my brain instead.
The direction of thinking was as follows: suppose we have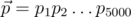
— a vector of probabilities of each bit being 1 (for convenience let's denote 
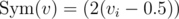). We can use these probabilities to sample queries somehow, and then update them somehow. How to estimate these probabilities? I tried to do it fairly, but failed: if queries depend on each other, it is too much pain. Instead I looked at it from a different angle. If we have query s1... s5000 and response l, it means that 
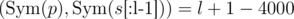and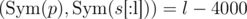 
((x, y) are dot products, s[:l] is truncated vector — python-style notation). So for q queries we have 2q linear equations which represent a hyperplane in 5000-dimensional space. We're interested in points within the cube [ - 1, 1]5000. Unfortunately, there can be plenty of such points. How to pick one? Intuitive assumption is that if we're treating all bits equally (which might be untrue due to the nature of the problem), we need some way which is symmetric over coordinates. So, I tried to just pick projection of 
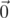on this hyperplane — it is symmetric and intuitively seems reasonable. (note: maintaining this projection can be done by smth similar to Gram-Schmidt orthogonalization and is expensive resource-wise; I didn't see many solutions with high working time on status page, so probably I was the only one doing this)
We get some estimation of probabilities of 0/1 on each position, but what to do with it? Natural idea is to sample queries based on these probabilities, but it doesn't work very well: the probabilities are too close to 0.5. I tried to address this by multiplying the probabilities by a constant in logodds space (i.e.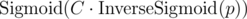
). This worked quite well: with constant C = 20 I got around 772 avg score on 1000 tests, and submitted this (getting 77571 on pretests).
Then, in the last hour of the contest, many participants started submitting solutions which were rather close to mine on pretests. And since the variance is rather high, it was possible that they're actually better than me, so I had to submit an ugly hack to get a better score. (As a matter of fact, I had this ugly hack prepared for a while, but didn't want to submit it because it is ugly). Once can guess that multiplying probabilities by 20 in logodds space is likely suboptimal. Instead we can introduce a (piecewise-linear) curve, and try to move its points and see if target score increases. This is tricky because the target score is random. I used fixed randseeds for tests and for sampling inside solution, and 1000 iterations to compute average score. Maybe it would work even better if we don't fix seeds and do smth similar to stochastic gradiend descent, but with 1k iterations computational resources are bottleneck. Nevertheless, such tuning gives ~+10 points (so avg score is ~780), and the solution with the ugly tuned curve gets 78465 points on pretests.
Looking at the scoreboard, there are plenty of solutions close to mine, which probably use different (greedy?) approaches. I really would like to know how do they work — are there any beautiful greedy ideas, or just hardcore tuning?
Thank you for sharing!
I like the vector interpretation, and how it helps to see and express the idea of orthogonalization.
Regarding information quantity, I'd like to note two points.
On one hand, we actually get ≈ 8.03 bits of Shannon information per query if we just calculate it by definition, so if we intend to learn some specific 1000 bits, we have only ≈ 803, so it won't be enough.
On the other hand, we don't want any fixed positions, any ≈ 1000 positions will do. Formally, of all 25000 possible bit strings, we would be satisfied with any one with 0 to 1999 errors. That's C[5000][0] + C[5000][1] + ... + C[5000][1999] ≈ 24849, so for some ideal way of classification, just 151 bit of information could be enough. Of course no one submitted such a solution, and getting any close to such ideal classification with reasonable complexity is perhaps impossible.
Мое решение: на каждом шаге беру случайный набор битов из первых ~4000 и инвертирую их. Если результат улучшился — сохраняю изменения. Для каждого бита подсчитываю "штраф". Очень простой вариант, типа
penalty[idx] += abs(dif) / count;, весьма неплохо работает, (тутdif— разница между текущим и новым ответом,count— размер измененной выборки.). Когда изменяю значение бита, меняю знак его штрафа. Больший штраф подразумевает то, что с большей вероятностью бит уже имеет правильное значение. Биты будем набирать случайно, но для каждого бита с положительным значением штрафа сделаем еще один тест на взятие, вероятность определяется текущим значением штрафа и текущей итерацией. Размер выборки константным делать не выгодно, он должен уменьшаться со временем. Коэффициенты функции размера выборки и функции вероятности взятия бита оптимайзил отжигом и руками (больше руками). В итоге средний результат = [4560 4763 4946].Yet another dumb solution:
Take 10 generation of 10 such requests: sort results of previous generation, merge first result with some others (I tried to merge with probabilities of the same ratio as first result to second in pair. Though this idea wasn't really successful and I stayed with equal probabilities), second with some and first with random string. First 10 are random strings, of course.
It's about 350 per test if you choose constants and params of merge wisely.
All in all, it was pretty interesting competition but random was too significant(?). I couldn't get proper strategy to improve results, just tried lots of random stupid ideas some of which all of a sudden brought me satisfying result.
Still I hope that these competitions will become regular on codeforces!
Решением #5 можно набрать больше. Я набрал около 696 с теста, на наборе претестов получалось то больше то меньше, но локально на 10000 тестах сходилось примерно к 696.3
После каждой попытки всегда бит, на котором упали ставим правильно. Это создает сложности в определении хороший блок или нет, но это получается выгоднее чем падать дважды на каком-нибудь бите. В таком случае для определения успешности инвертирования будет сравнивать с ожидаемым результатом. Если предыдущий результат был result, то после неудачного инвертирования ожидаемый результат увеличится на 1.5. Ну и если было успешное инвертирование, то ожидаемый результат записываем заново, как результат с текущей попытки + 1.5. 1.5 — это только что выставленный бит и еще один угаданный, потому что продвинулись дальше.
Константу нужно брать 41. Инвертировать имеет смысл только порядка первых 4000 бит, не знаю как доказать, но на графиках видно, что при таком подходе, начиная где-то с 4060 ого бита между выставленными наверняка (полученных с результатов попыток) остается много правильно стоящих бит.
Для некоторой длины инвертированного блока можно посчитать математическое ожидание дисбаланса в нем, и тогда блок нужно взять такой, чтобы 99 * M(X) было максимально, и X * 99 не переваливало за некоторую границу. По факту я брал некоторые блоки по 43, некоторые по 39, считал их "рюкзаком"
I wasn't able to get more than 510 per test in average with this solution, it's pretty simple anyway.
Divide given string into parts (I've chosen 25 parts of 200 bits each), try random substring on part several times (for 25 it was 100 / 25 = 4) and select best of these. And save wrong answers every time.
One minor improvement to Solution 7 is to do segment inversion with segments of variable size, the size of which depend on the amount of bits at the present pool at your disposal. The present pool is updated at each query with the new bits visited. This amounted to a tiny improvement with respect to fixed size.
Please! Look the status!
I want to share my easy solution. It's very short. It's 68000-70000. 18629511
Seems that CF contest rating is irrelevant on maraton contest. Look the color mixed on scoreboard.
People who have more free time have the advantage even if their skills are equal. It's what happens when a contest lasts for several days. I don't have a lot of free time, so I don't see a point to take part in such long marathons at all.
However, if the duration was 4-5 hours, I'd participate. The results would be far more relevant, and it's surely more fun — to write something working in deadline conditions. So, how about holding such contest?
During 4-5 hours it is impossible to generate and test many ideas. So it will be too random competition about how lucky you are in your first guess. Actually our team spent about 10 hours in total (and last three hours were useless), but may be we were lucky and it could take more time.
The problems for short marathons could be simplier. And after 20-30 contests any randomness will disappear, just like in Codeforces Rounds.
Take
MarathonDeadline24, for example — they have 2 marathon-style problems for 5 hours in the qualification round, just as I suggest, as one person usually codes one problem there. Nobody complains and everyone is happy with it.In codeforces rounds there is a lot of randomness =)
I am not sure, that there will be enough problemsetters for 20-30 well designed problems for 5 hours.
At last Marathon24 they have 5 marathon-style problems for 5 hours. And it was huge random. But it was ok because for top teams it was easy to get into top-30 and qualify.
May be you are talking about Deadline24. It was even more huge random, because they gave problem very similar to past problem from TCO Maraphon. Everybody who participated (for example I) got huge advantage.
Why do you say there's a lot of randomness in Codeforces rounds? What make Codeforces rounds different from another competitions. Or do you mean there's a lot randomness in competitive programming contests in general?
Variance is inversely proportional to the duration of the contest. Acm-style team contests are less random at least due to bigger duration.
There are already a lot of contests that have 4-5 hours duration. It's pretty cool to have something different. Your idea sounds interesting as well, but it's nice to have more marathons that last for 10 days, where you can solve 1 problem without being stressed out by tight contest duration restrictions. I enjoyed this marathon so much, so props to authors and I hope to see more of that stuff in future + maybe separate ranking for marathons.
I mean 4-5 hours marathon contests. How many of them do you know? I know only Marathon24 / Deadline24 qualification.
I understand that. I don't know about 5 hour marathons. What I wanted to say is that format when you have to stay concentrated on solving problems for 5 hours is very common, but I personally prefer much longer duration and more chill process. Anyway, it would be nice to have 5-hour marathons here as well and compare (5 hours vs 10 days) community feedback.
There is also first day of Wide Siberian Olympiad. It is an onsite contest though, and the problem is in Russian only.
Google Hash Code
Any info on the T-shirt winners?
Marathon still have no status "ended". I think something will be changed.
The results are final. Congratulations to the winners!
778886) ilyakor774606) savsmail772473) hakomo770837) Nicolas16759469) MrDindows744666) aimtech: zeliboba, yarrr740863) PalmPTSJ739006) HellKitsune728997) IPhO728961) haminhngocThe program used to generate random T-shirt winners: code on IdeOne.
(16) Andromeda Express: ainu7, Astein
(55) Mediocrity
(85) quailty
(97) Kniaz
(101) waterside
(134) SteelRaven
(158) khadaev
(182) Thr__Fir_s
(184) Simon
(188) GoogleBot
Also, thanks to everyone participating! Good to see that people are interested.
Cool contest!
Omg! Omg! How lucky =D
Was the seed
12345somewhere in the contest announcement?Or was it chosen arbitrarily after the contest?
Next time if you forgot to mention the method of drawing you can use a seed from the future from random.org.
No, but seed
12345appears in example solutions, which somewhat reduces the arbitrariness.Do you mean random.org provides random numbers which can be requested in advance but become available only after specific point in time? I don't see such option.
Other than that, yeah, it's better when the exact way of generating the random sequence is announced in advance but still cannot be abused. Sorry it didn't happen this time.
https://www.random.org/sequences/?mode=advanced
Use pregenerated randomization from (date)
Determine the earliest date that is NOT available yet (currently it is 2016-06-24). Announce this date to the participants. Then tomorrow go back to random.org to make the draw.
Or similarly you can just generate one seed integer using https://www.random.org/integers/?mode=advanced but then you also need to announce the min and max.
Something like this, for a date after contest end? Got it, that's neat, thanks for showing!
Min (11) and max (201) can be determined by Update 2 in the original post, once the results are final.
I haven't seen the problem statement. Can someone post a link?
Sure.