Приветствую всех участников раунда!
Давайте проведем разбор задач в примерном порядке их сложности
182B - Vasya's Calendar
Обратим внимание, что Вася должен вручную прибавлять номер дня только тогда, когда заканчивается один месяц, и начинается следующий. Значит, пусть у нас в текущем месяце было x дней, а в следующем уже y. Тогда в первый день следующего месяца часы будут показывать день x + 1 (не забываем про модуль d), а должен показывать номер 1.
Очевидно, что Вася должен вручную прибавить d - x дней, чтобы часы показывали то, что нужно.
Значит, ответ — это сумма всех чисел d - ai, где 1 ≤ i < n.
182D - Common Divisors
Эта задача решается многими способами, но самый простой подход следующий: найдем все делители строки s1, все делители s2 и найдем пересечение этих двух множеств.
Как же найти все делители строки? Пусть t — это делитель строки s. Тогда очевидно, что |s| = 0(mod|t|), а также t является префиксом строки s. Эти соображения и позволяют найти все делители строки, а именно переберем длину префикса, проверим делимость, а потом проверим, что префикс записанный подряд нужное количество раз совпадает с s.
Всего подходящих префиксов не более 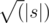 , проверка каждого работает за O(|s|), значит, итоговое решение за
, проверка каждого работает за O(|s|), значит, итоговое решение за 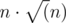 , где n = max(|s|, |t|).
, где n = max(|s|, |t|).
Найти пересечение двух множеств строк несложно, можно воспользоваться стандартными структурами данных
182E - Wooden Fence
Условие задачи было сформулировано неверно, что привело к несоответствию решений, правильный вариант условия появится совсем скоро, приносим участникам свои извинения.
Основа решения этой задачи — это динамическое программирование.
Состояние — (last, type, l), где last — номер последней доски, type характеризует поворот последней доски, а l — длина оставшейся части забора.
Пересчитывать эту динамику тоже очень просто: переберем номер следующей доски, ее поворот, проверим подходит ли она в текущее состояние, и прибавим нужную величину.
Асимпотика решения — O(n2·len).
182C - Optimal Sum
Представим мысленно задачу в виде движения слева направо некоторого окошка длины len по исходному массиву. То есть нам нужно найти способ достичь максимума в выбранном окошке, а потом сместить его на одну ячейку вправо.
Пусть мы зафиксировали положения окошка, теперь посчитаем ответ. Для этого отдельно запишем все положительные и все отрицательные числа в окошке. Если положительных не больше, чем k, или отрицательных не больше k, то мы можем все числа сделать одинакового знака, и ответ — это сумма модулей чисел в подмассиве. Это простой случай.
Несложно понять, что невыгодно некоторые отрицательные числа делать положительными и одновременно некоторые положительные — отрицательными. То есть мы обязательно выберем знак <<+>> или <<->> и k чисел этого знака сделаем противоположными. Также несложно понять, что всегда при смене знака у некоторых чисел выгодно брать ровно k максимальных по модулю чисел этого знака.
Для того, чтобы поддерживать движение окошка будем использовать два отдельных дерева отрезков: одно для отрицательных, другое для положительных чисел.
Если в вершине дерева хранить пару (количество чисел в поддереве, сумма этих чисел), то такая структура умеет возвращать сумму k максимальных чисел, что нам и требуется.
Асимптотика решения — O(n·log(n)).
182A - Battlefield
В этой задаче есть два главных момента:
длина любой траншеи в метрах численно не превосходит b
траншеи не пересекаются
Первый пункт означает, что если Вася забегает в траншею чтобы переждать, пока лазер работает, то за это время он может придти в любую его точку.
Второй пункт означает, что пока лазер работает, Вася обязан находиться в той траншее, в которой он на данный момент сидит.
Значит, путь Васи — это перебежки от одной траншеи к другой, где он пережидает лазерную атаку. Таким образом все решение задачи — это найти кратчайший по времени путь по траншеям от стартовой точки до конечной (их мы тоже будем считать траншеями, просто нулевой длины), для этого нужно всего лишь предподсчитать матрицу расстояний между отрезками траншей и запустить алгоритм, например, Дейкстры.
Два тонких момента:
мы не можем перебегать между траншеями, если между ними расстояние больше a
пусть Вася прибежал в момент времени t, теперь нам нужно найти момент, когда он сможет убежать дальше. Для этого нужно найти следующий момент времени, когда лазер будет перезаряжаться. Эта величина T несложно ищется по формуле:
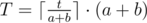
Асимптотика решения — O(n2).











задача С.
Не очень понятно, как написать дерево отрезков, умеющее возвращать сумму k максимальных чисел? Если честно, весь разбор очевиден, а самое интересное вы опустили..
Если учитывать что в больших ячейках лежать большие числа, то просто:
- делаем спуск по дереву с параметрами (вершина, сколько нужно набрать)
- если вершина содержит меньше нужно кол-во чисел то берем их все
- иначе спустимся в левое поддерево, а потом в правое(и в обратном порядке, если ищем максимумы)
- в случае если пришли в вершины с кол-вом 0, то просто вылетаем с процедуры
Это делается одним спуском по дереву отрезков сверху вниз. Дерево отрезков построим над числами (например отрицательными) как над отсортированным множеством элементов. Для каждой вершины мы храним две величины — кол-во чисел в отрезке и их сумму. Пусть мы стоим в некоторой вершине дерева и хотим взять cnt максимальных элементов. Тогда если в правом поддереве меньше или равно cnt элементов пойдем в правое поддерево и возьмем их оттуда. Иначе возьмем целиком правое поддерево в ответ (то есть сумму в нем), а в левом поддереве попробуем взять оставшуюся часть элементов.
Прочитал ваш коммент и предыдущий и так и не понял, как сделать такое дерево. У нас же последовательность по условию не отсортирована. Тогда не будет никакой закономерности, в какую ветку идти. Или как?)
Делаем сжатие координат и используем значения в качестве индексов.
Ну пусть дана последовательность 1 10 7 3 5
Отсортируем ее по убыванию: 10 7 5 3 1
Дадим нашим числам индексы, 10 — 0, 7 — 1, 5 — 2 и т.д. Можно сделать через map. Сделаем так называемое сжатие координат.
И на этих индексах построим дерево отрезков. В листьях дерева отрезков будем хранить сколько каждого числа взято и сумму. А остальные вершины дерева отрезков уже нетрудно пересчитать.
Когда идем по исходной последовательности, по числу получаем его индекс и увеличиваем / уменьшаем в дереве отрезков кол-во этого числа и сумму.
да, теперь понял
только у тебя приоритет всегда налево
Все, большое спасибо, понял
тож не понял.
Кто понял? Можете объяснить? Все таки интересно...
Да не нужны никакие деревья отрезков)
Для начала избавимся от модуля в формулировке задачи — представим, что его нет, найдем ответ, умножим все числа на (-1), найдем ответ, выберем больший.
Как находить ответ — положительные числа берем всегда втупую, для отрицательных храним два сета — сет k наименьших и сет для всех остальных. При добавлении/выкидывании в окно аккуратно правильно поддерживаем эти два множества и пересчитываем ответ.
С другой стороны, если вы умеете быстро и правильно писать нужное дерево отрезков, наверное вы напишете его быстрее, чем эту магию с множествами — там есть где наошибаться.
Ну обычно такие задачи, где окошком нужно иди, решаются одним из этих способов, но на пасе тяжело сет закодить.
А почему ты пишешь на паскале?
Нужно опыт иметь. Изза С++ много слетов, не знаешь где она как себя поведет.
В таком случае предлагаю вам попробовать Java =)
можно не пользоваться STL. реализовывать все самому. и поучите тот же паскаль..
Можно использовать кучи... их на пасе уже попроще написать.
а как обойтись без удаления из произвольного места? Ведь при сдвиге "окна" вправо, нужно удалять элемент, который не обязательно лежит наверху...
Можно для каждого элемента в куче всегда хранить, где он в ней находится, тогда удалять можно.
спасибо
за это и люблю самописанные кучи...
По идее можно просто лениво удалять, так еще проще. Просто если мы достаем из вершины кучи какой-то элемент и видим, что его нужно было удалить раньше, то просто забиваем на него и достаем следующий. Это гораздо проще кодится, правда у нас будет в куче храниться больше нужного элементов.
У меня обычно это проблемно пишется, есть частные случаи, всегда приходится писать чекер, что-бы проверить не набажил-ли где-то.
А какие там частные случаи? Вроде в моей реализации их нету.
Когда удаляешь последний элемент из кучи, например. Не знаю как ее пишут остальные, но у меня вечно как-то сложно выходит.
Вот моя реализация полуторалетней давности : http://pastebin.com/DcRssr37
Странно, написал также и словил TL.
Посмотрел твой код — похожий и зашёл за 220 мс.
Подскажите, пожалуйста, что не так!
count мультисета в худшем случае работает за O(n). Истина.
Попробуйте заменить строчки вида
if (s.count(x)==0)на что-то вродеif (s.find(x)!=s.end())UPD. Хотя если написанное выше — ложь, то это вряд ли поможет.
UPD. А раз все-таки правда, то может и поможет. Hohol, хватит делать правки =) Мое решение с сетом пар вместо мультисета зашло за 160 мс. Мультисеты вообще мутные какие-то.
Ну почему мутные? Легко понять, почему в худшем случае за O(n) работает...Хотя может там и не такая реализация, как я предполагаю.
Да чего мутные, надо лишь знать, что count долго работает и
s.erase(val)удаляет все вхожденияval. Больше проблем не встречал.Не долго, а столько сколько нужно плюс O(log(n))
O(Log(n)+k), где k собственно количество.
Я его использовал просто пару раз всего. Обычно гораздо надежнее и проще завести map<значение, сколько раз встречается>. Тут ни с count() никаких проблем, ни с удалением.
Ну это уже дело вкуса, вот мне удобнее было сделать сет пар со вторым значением id, кому-то мультисет больше нравится. Каждый участник исходя из своих особенностей и опыта выбрал для себя свой вариант, который ем упоказался более надежным, или например быстрым, или такой что накосячить сложнее, или просто от балды что первое пришло в голову, чтобы не отвлекаться от сути задачи на детали реализации. У всех свои предпочтения.
Да, конечно. Я не имел в виду, что map/set рулит, а multiset для дураков. Я имел в виду, что так "надежнее и проще" лично мне. Кстати эту задачу я сдавал сетом пар.
Сдал за 140 мс.
Спасибо за помощь Hohol, Tranvick и всем кто не прошёл мимо!
не зная такого дерева отрезков, можно было решать деревом фенвика + бинпоиск, перебирать бинпоиском на каком месте стоит к-й максимальный элемент и проверять фенвиком, правда сложность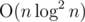 , ну тоже сойдет
, ну тоже сойдет
Расскажите поподробнее
А почему в E меняется условие, а не авторское решение?
Так просто проще.
Ну да, проще сделать контест нерейтинговым, а я так старался..(
В следующий раз еще постарайся. Харош ныть
обидно )
А ты не всегда стараешься на контестах?
'а я так старался'-означает что на этот раз старался по-особенному, потому что нужно было доказывать то ,что я обгоняю одноклассников по рейтингу не случайно...
Первоначально задача выглядела как сейчас. Однако затем были внесены неправильные правки и она стала пониматься по-другому. В исправленной формулировке решение совпадает с пониманием.
В задаче C есть решение без дерева отрезков. Предположим, что хотим менять только положительные элементы на отрицательные (другой случай рассматриваем аналогично). Поддерживаем два множества (
setв C++)activeиpassive: в обоих храним элементы (a[i], i). Вactiveдля окошка в данный момент храним те положительные элементы, которым мы поменяли знак; вpassive— остальные положительные элементы. Сумма для данного окошка — модуль от: сумма всех чисел изactive, взятых с отрицательным знаком, плюс сумма всех остальных элементов. Двигая окошко, один старый элемент выходит, и один новый появляется. Текущую сумму всех чисел, а также оба множества можно тогда обновить за логарифмическое время при смене окошка.опа
Наверное вместо того, чтобы хранить пары лучше использовать мультисет...
ага
Из мультсета удаление какое-то странное, хотя это вроде бы решается удалением по итератору.
Да, при удалении удаляются все элементы с таким значение... и да, при удалении итератора удаляется только один элемент...
Кто знает как решать Е со старым условием? Час пытался придумывать, вот и интересно.
А что там была за задача?
Там говорилось, что заборы отличаются только если отличается последовательность типов древесины, из которых сделаны доски, а это создаёт сложности для квадратных досок, а также сложности для стартовых положений досок, ибо какое-то состояние в таком случае может два раза посчитаться, если я правильно понимаю все проблемы этой задачи. Это были мои сложности при её решении, и эти соображения не предентуют на истинность.
Опять же мне кажется, что все проблемы рашаются исключением квадратных типов досок, и авторское решение станет верным.
Нет, как раз квадратные тут ничего не портят.
А разве это не есть таже-самая задача, или я чего-то не понимаю?
Ну написано что условие обновят в скором времени, видимо не обновили еще, я не перечитывал.
Уже было. Решаем ее с новым. А далее надо вычесть лишние последовательности. В каком случае мы получаем лишнюю последовательность? Очевидно только в случае, если две доски из разной древесины имеют одинаковые размеры (axb и axb или axb и bxa) и длина забора делится на (b+a). Далее есть несколько способов; самый простой — тупо перебрать все пары типов древесины и повычитать единички, если находится плохая пара. UPD Прощу прощения, написал бред.
challenge:
судя по всему — нет
По-моему в задаче D можно было решить линейно(по крайней мере у меня зашло) Представляется понятным факт, того что у каждой строки есть единственный префикс минимальной длины,который является ее "делителем". Найти его можно за O(len(s)). Т.е. по сути сжать строку, теперь она будет состоять из N одинаковых элементов. Теперь сравним эти префиксы для двух строк, если они различны, то ответ 0. Дальше найдем gcd(N1, N2) и за корень найдем число его делителей, что и будет ответом. Получается линия.
Моё решение за линию работает, из-за хешей.
D решается линейно при помощи префикс-функции.
D можно решить за линию при помощи перебора делителей длин строк...