Изначально мы хотели расположить задачи по сложности так: A-C-E-D-B. Насчет порядка последних двух мнения разделились. Посмотрим, что покажут результаты.
В этой задаче нужно сделать то, что написано в условии — отсортировать команды по заданному компаратору: (p1 > p2) или (p1 = p2 и t1 < t2). После этого надо разбить команды на группы одинаковых, и найти размер группы, команды из которой делят k-ое место. Многие почему-то при равенстве числа задач сортировали команды по убыванию времени, а не по возрастанию. Такие решения случайно проходят претесты и получают WA #13.
Так как многоугольник A — выпуклый, достаточно проверить, что все вершины многоугольника B лежат строго внутри многоугольника A. Идейно самое простое решение – построить выпуклую оболочку из точек обоих многоугольников, и проверить, что в нее входят точки только из первого многоугольника. Но в таком решении придется писать выпуклую оболочку, которая обязательно берет все точки, лежащие на одной прямой, а это на порядок сложнее других решений и содержит частный случай.
Второе решение – разрежем A на треугольники (по номерам вершин): (1, 2, 3), (1, 3, 4), (1, 4, 5), …, (1, n - 1, n). Последовательность углов 2 - 1 - 3, 2 - 1 - 4, 2 - 1 - 5, …, 2 - 1 - n монотонно возрастает. Значит, для каждой точки многоугольника B можно за log(n) бинпоиском найти, какому треугольнику она может принадлежать по углу относительно вершины 1.
Аналогично можно разрезать многоугольник A вертикальными линиями на O(n) трапеций. В таком случае бинпоиск будет просто по x-координате.
Если в исходном массиве нет числа x, то, очевидно, нужно его добавить, +1 к ответу. Далее делаем следующим образом. Пока медиана массива строго меньше x, нужно ее увеличивать. Очевидно, самый надежный способ увеличить медиану – добавить в массив максимальное число (105). Аналогично, пока медиана строго больше x, добавляем в массив числа 1. Ограничения позволяют добавлять числа по одному и пересчитывать медиану “в лоб”.
Также есть решение вообще без случаев: пока медиана не стала равна x, добавляем в массив число x.
Будем рассматривать всех людей в порядке убывания их размера обуви. Заметим, что при рассмотрении i-го человека нам важны максимум две пары обуви: размера li и li + 1. Это позволяет написать динамику с состоянием: (номер первого нерассмотренного человека i, доступна ли для покупки обувь размера li, доступна ли для покупки обувь размера li + 1). Переходы: оставить i-ого человека без обуви, или продать ему обувь одного из двух подходящих размеров.
Очевидное решение динамикой: нам важно только сколько ходов осталось сделать муравью, и в какой из четырех вершин он стоит. Получается 4n состояний, из каждого по 3 перехода – при аккуратной реализации такое может пройти. Можно заметить, что вершины A, B, C эквивалентны между собой. Это позволяет написать такое решение:
int zD = 1;
int zABC = 0;
for (int i = 1; i <= n; i++) {
int nzD = zABC * 3LL % MOD;
int nzABC = (zABC * 2LL + zD) % MOD;
zD = nzD;
zABC = nzABC;
}
cout << zD;
Также задачу можно решать за log(n) бинарным возведением в степень n некоторой матрицы 2 × 2.
Ничего себе "случайно проходят"!
Спасибо за разбор. На Д писал такую же динамику, вылезли проблемы со случаем, когда делался переход по типу:
Тест: 3 пары (1-1, 1-2, 1-3) 3 покупателя (1-1, 1-1, 1-2) Динамика начинает ошибаться в таком месте:
3-ий человек покупает для себя обувь своего размера. переход в предыдущий максимум, где: 2-ой человек покупает для себя обувь своего размера. переход в предыдущий максимум, где: 1-ый человек покупает для себя обувь на размер больше.
Моя программа выдает:
3 1 2 2 1 3 2
Выходит что 1-ый и 3-ий купили одну и туже обувь!
Я не правильно строю переходы? Помогите, пожалуйста! (вот код: 1395703)
А как проверить лежит ли точка внутри треугольника?
Берете сумму трех треугольников ( каждый из которых — это одна вершина — наша точка, две другие — вершины треугольника) если эта сумма равна (примерно) площади треугольника то ДА иначе НЕТ.
Используй Google, Люк...
Ни за что!
В задаче E у матрицы хорошие собственные значения, значит есть простая формула через какие-то степени чисел.
UPD: а именно
, как и было замечено ранее
можно небольшой вопрос, про задачу B. Она у меня упала на 22 тесте. Числа в тесте превышали 10^9, хотя в условии было сказано, что числа <10^9. Почему так?
показалось)
Возможно при умножении происходило переполнение.
я не использовал умножение. Скорее всего, на следующих тестах программа упала бы...
Так у Вас ошибка времени исполнения — выход за пределы массива.
точно,забыл при объявлении нолик дописать
B наверное можно решить немного быстрее: за MlogM+N(M-количество вершин внутреннего многогульника)
Нужно заметить ,что точка входит в многоугольник тогда и только тогда, когда существует сторона, которая ниже этой точки и сторона, которая выше этой точки(в обоих случая вертикальная проекция точки лежит на стороне). Отсортированный по X список сторон можно получить за O(N) исходя из того факта, что стороны заданы в порядке обхода по часовой стрелке,а точки внутреннего многоугольника отсортировать по X за MLOGM.
Далее, пройти по отсортированным по X сторонам и выкидывать/добавлять из очереди точки,которые проецируются/не проэцируются на cоответствующую сторону. Для каждой точки проверять выше или ниже она рассматриваимой стороны. Так как для выпуклого многоугольника существует максимум 2 стороны на которые проецируется какая либо точка,то всех таких проверок будет O(N).
После прохода проверить,что мы нашли хотя бы одну сторону которая выше и хотя бы одну сторону которая ниже для каждой точки второго многоугольника.
P.S Правда,я это не сдал,где то баг:)
UPD: Сдал. Правда не совсем так,но суть не поменялась:) Это же надо руки такие кривые , компаратор неправильно написать.
Что-то подобное сдал я. Только проще идти по точкам многоугольника B, для каждой из которых будет только одна сторона многоугольника A, на которую указывает текущий вектор. Можно поддерживать указатель на такую сторону с суммарной сложностью O(N + M). Вектор можно проводить из любой точки, которая находится внутри многоугольника A. Такую точку можно найти в целых методом неадекватного извращения (если можно проще, то дайте знать). Умножим все координаты обоих многоугольников на N (количество вершин в многоугольнике A). Затем найдем сумму значений по каждой из координат и разделим на N — вот и искомая точка. Теперь, при поиске векторного произведения у нас будет происходить переполнение 64-битного целого, но метод извращения предусматривает и это! Для любого вектора при векторном произведении мы будем выполнять деление его координат на N. Теперь у нас есть решение в целых и ничего не переполняется. Теперь нам остается написать все это безобразие и люто молиться весь систест.
А почему в В нельзя просто проверить лежит ли каждая точка второго внутри первого?
TL будет ,2000 000 000 операций
А если за logN проверять, то можно, проверено.
Edited -- Fixed my code! Thanks to Igel_SK!
Isn't the state for D too big?
Also, I see people doing bipartite matching in a greedy way, why does this work?
Bipartite matching with sorting shoes works correctly, it can be proofed (in russian). I think it should get TLE but the tests were weak :)
I solved with the DP this way: you have the current person and a mask that represents if the 2 sizes of shoes that this person can use are available (costumers are sorted by shoe size), so it will be a dp[10⁵][4] table.
I solved E:Tetrahedron using the problem (3^n+3*(-1)^n)/4 . Here is my solution . However it failed the system test and when I used BigInteger it passed.Here is the 2nd version. 2 question: 1.Why does the first solution fail... 2.Is there any thing I can do to avoid BigIntegers
Use
longDoubles are not accurate
Your code with long instead of double 1403711
Got the same problem.
how did you arrive at this formula can you please explain??
do the adjacency matrix A (in this problem you will have a matrix where A[i][j] = 1 if i!=j and A[i][j] = 0 if i==j). now A^2 count paths with two edges, A^3 count paths with three edges and so on, do exponentiation using diagonalization i.e A = P*D*P^(-1)
A^n = P*D^n*P^(-1)
You have to find a formula for one element on the diagonal using matrix P, D^n and P^(-1), just there you will notice the formula (3^n+3*(-1)^n)/4. (all of elements on diagonal are equal for this reason you need to find the formula of only one of them)
be carefull doing division using modulo, here you will find good information of how to do that https://codeaccepted.wordpress.com/2014/02/15/output-the-answer-modulo-109-7/
I don't understand how A^2 counts paths of length 2 and A^3 counts paths of length three etc. Am I missing some concept?
mod function in my code is not working
include <bits/stdc++.h>
using namespace std; //#define int ll; // [9,223,372,036,854,775,807 to -9.....808] 19 digits
define pb push_back
define all(x) (x).begin(),(x).end()
define mp make_pair
define vii vector < int >
define pii pair < int , int >
define vpi vector < pii >
define fi first
define se second
define mem1(a) memset(a,-1,sizeof(a))
define mem0(a) memset(a,0,sizeof(a))
define rep(i,a,b) for(int i=a;i<b;i++)
define repit(st) for(auto it=st.begin();it!=st.end();it++)
define sz(x) (int)((x).size())
define len(x) (int)((x).length())
template<typename T,typename T1>T amax(T &a,T1 b){if(b>a)a=b;return a;} template<typename T,typename T1>T amin(T &a,T1 b){if(b<a)a=b;return a;}
//const int mod=998244353; const int mod = 1000000007; const int N=1000000+6;
define M_PI 3.14159265358979323846
const int maxn=1e5+5;
int main() { ios_base::sync_with_stdio(false);cin.tie(0);cout.tie(0);
int n;cin>>n; int abc=3,d=0,abcp=3,dp=0; rep(i,2,n+1) { abc=((dp*3)%mod+(abcp*2)%mod)%mod; d=abcp; abcp=abc; dp=d; } cout<<d;}
can you plz tell me why??
What 2 x 2 matrix can be used in E? I've only seen it solved with a 4 x 4 matrix with diagonal = 0 and rest = 1.
See Egor's solution: 1390234
Can you explain the idea behind this solution?
In general, you can do matrix exponentiation (that is, raising matrix M to the N-th power) in
O(logN)time, where N is the exponent. If you exploit a "matrix notation" for your dp recurrence, then you can reduce it to this problem, thus solving it inO(logN).For example, it is possible to find the N-th fibonacci number using this method. For a better explanation, check out the "Fibonacci log N" tutorial on e-maxx.ru
let A be a matrix of 4X4 where,
A[i][j] = 1 if i != j, and 0 otherwiseNow, A represents the number of paths from i to j using 1 edge. Using some basic intuitions we can prove that A*A will represent the same but using 2 edges. So, we can A^n will represent all the paths from i to j using n number of edges. Now, you can exponent it or derive a formula. I derive a formula, see it here 51966083
Thank you for the explanation! Can you share a proof also?
Sorry about that, just ignore the post.
from math import *
def fast_exponentiation(base, n): if n == 1: return base else: if n % 2 == 0: base1 = fast_exponentiation(base, n/2)**2 return base1%1000000007 else: return (base*fast_exponentiation(base,(n-1)/2)**2)%1000000007
t = int(raw_input()) if t%2 == 0: print ((fast_exponentiation(3,t) + 3)/4)%1000000007 else: print ((fast_exponentiation(3,t) — 3)/4)%1000000007
Why is this code in Python wrong for thetraedron?
Note: you can use the built-in function
powfor fast modular exponentiation:I keep getting wrong answer...
I get right values if I put modulus outside all the expression, so:
print ((fast_exponentiation(3,t) + 3)/4)%1000000007 gives correct value, but slow and print ((fast_exponentiation(3,t) + 3)/4) within the fast exp with mod gives WA, why?
You can't divide by 4 if you use mod before it. You should multuply pow(4, p-2, p) instead
Try ((fast_exponentiation(3,t) + 3) * 250000002) % 1000000007, and take modulo on each fast_exponentiation step.
ant.ermilov thank you for the tip, I have seen it in a solution as well, but can you explain to me, or point me to somewhere that can tell me, why is that particular number used?
At first, let's try to understand, why your approach does not work. For example, we have
Y = M+1, Y % M = 1,
but (Y / 4) % M != (Y % M) / 4.
So division can be substituted by multiplication. In general, we have modulo M, divisor D and want to find such Z that for each X: (X / D) % M = ((X % M) * Z) % M.
After simple transformation we will get (X * Z) % M = 1.
For particular case 250000002 * 4 = 109 + 7 + 1.
Some extra info: Z can be found iff gcd(X, D) = 1, and simpliest way described at riadwaw's comment above. From Euler's theorem we get Z = (DM - 2) % M.
Amazing explanation! Thanks
What does non-degenerate mean in 166B - Polygons (Div2 B) ?
Found myself : link
@riadwaw Can you please explain In the solution to E why has nzABC been multiplied by 2 in the fifth line?
int nzABC = (zABC * 2LL + zD) % MOD;Thanks a lot.
Let Ai denote number of ways to finish near the vertex A after i moves (same for Bi, Ci, Di). Easily,
with the initial conditions
Due to the symmetry $A_i=B_i=C_i=ABC_i$, so
Nice Explanation :)
I'm interested in E,whether there is any simple formula without matrix.i can't get it,anybody got it and coubld you share it?
CAN anybody explain E in detail? Can't get it.Thanks!
Let f[A][j] is the number of ways from D to A by going j steps,as same,f[B][j], f[C][j] and f[D][j], we know f[D][0] = 1, f[A, B, C][0] = 0(because the ant starts at D).
then you get four equations below:
f[A][j] = f[B][j - 1] + f[C][j - 1] + f[D][j - 1]
f[B][j] = f[A][j - 1] + f[C][j - 1] + f[D][j - 1]
......
f[D][j] = ...
you can solve this problem in O(n),the answer is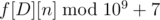
.
but it's too slow.you can express the four equations by matrix.then it's obvious to solve the problem by Successive Square Method with matrix in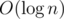
.
Thank you, I finally understood it!
@RAD In question B Polygons, What's the problem if we directly compute the convex hull of all points and check if any point of B is present in it ? I couldn't understand the mistake!!
I was able to solve Div 2 C Median using an O( 1 ) approach. Submission is here: https://codeforces.me/problemset/submission/166/52647089 .
Basic Idea: We have to ensure that the element we have to make as median (x) has to be at the central position. Now there can be 3 types of elements obviously: (i) smaller than x (ii) equal to x (iii) larger than x
Note that there can be duplicates so the number of elements equal to x can be more than 1 (or even 0). Our final aim is to ensure one of the elements equal to x lands up at the central position at the end. We know that in the final answer, 0 <= number of elements on right of median — number of elements on left <= 1 In case there are more than one equal elements, we can observe that the optimal answer will always have more of the extra equal elements on the side with less number of elements ( smaller or larger ). And the situation will look like this:
Now we have to find the number of elements that need to be added: Case 1: When number of smaller elements < number of larger As the left side can have one lesser elements than the right, number of elements we need to add is (elements greater than median — elements less than median — (elements equal — 1) — 1). Why elements equal — 1 ? Because one of these elements shall be at the median position. Obviously, it can't be less than 0, so we have to max it with 0. And also we subtract an additional -1 as we are allowed to have left side smaller.
Similarly we can devise Case 2 and 3 where elements on both side are qual or smaller > larger. I guess code will be able to explain itself better now !
For 166 C — Is their a direct mathematical (formula based) approach in which we dont have to use a loop once we have taken the input?
In case someone did not understand the editorial of 166E — Tetrahedron, here is a simple way of looking at the solution : zD is the number of ways of reaching D in
isteps and zABC is the number of ways of reaching A or B or C inisteps(A , B, C are equivalent points). Since the ant starts of from D, initially (ati = 0)zD = 1andzABC = 0.Now in each subsequent step, 2 things can occur :
If the ant was at D, it will come down to any of the A,B,C points. That means it has 3 options. Hence , nzABC = zD.
If the ant was at either of the A,B,C positions, it can either climb upto point D or go to any of the 2 other equivalent points i.e. if the ant was at A, it can go to D and hence nzD= 3*nzABC ; or it can go to either B or C (2 available options) which increases nzABC by 2*zABC and hence nzABC += 2*zABC.
Therefore at last
nzABC = 2*zABC + zDandnzD = 3*nzABC.I am getting TLE in problem E,i am using dp approach.Anyone please help code submission: https://codeforces.me/contest/166/submission/88417439
declear dp array globally then you will not be needed to make whole array zero .may be thats why you are getting tle
here is my code for 166E. Tetrahedron 105550054
My code is giving a time limit exceeded for the test case with n = 10000000. But when I change the vector with an array, i.e. in 105550845 It is running much faster and got accepted! Why is this problem with vectors? Why is the vector so slow? I am new here :)
this should pass
UPD: sorry I miss understood your question :)
I think it's because you're creating n unnecessary vectors while you can just creat 1
see the code above it's faster and with vectors :)
Thanks Satoru for your answer! :) I got it accepted using your correction. But still it is taking more time than with the array one. So vectors are really slow?
Yeah arrays are faster
But like a lot of people I'm not using arrays (I just use vectors) because it have benifiets more than arrays (like push_back, pop_back ... etc) and you don't need to calculate the size, just use
resizeunlike arraysHow did solutions based on Kuhn's algorithm passed in problem D? Shouldn't it get TLEd?
In problem B, how can we find the convex hull of points if there might be three or more points on the same line?
My soln for E:- Notice-its easy to notice we need total strings of length n+1 starting with d and ending with d and can have alphabets {a,b,c,d} such that no same alphabets can be consecutive. Now noting that we just need strings with a/b/c ending with a/b/c ans yeah of course no 2 same alphabets consecutive and must have length n-1. Lets denote x_n such strings with length n so if first character is a then a.......(a/b/c) now 2nd character can be b/c/d,if its d its obvious to notice we can first find such strings of length n-2 and concatenate string ad with is hence x_(n-2) strings of such type, if its b/c we can find such strings of length n-1 and argue by symmetry there will be exactly 2/3 of such strings hence 2/3*x_(n-1) hence if first charcter is a we say total=x_(n-2)+2/3*(x_(n-1)) strings and hence by symmetry again same for b and c hence total strings=>x_n=3*x_(n-2)+2*x_(n-1) this can be solved using generating functions which gives us x_n=(3*(-1)^n+(3^(n+1)))/4; we need x_n-1=(3*(-1)^n+(3^n))/4
For problem A, You could also save the pair of numbers by subtracting the second number by 51 as it would help in sorting in descending order. For ex there are two pairs (5, 3) and (5, 4) according to problem (5,3) must come before (5, 4) but by sorting in descending order (5, 4) would come first and then (5, 3), but by saving the pairs as (5, 51-3) => (5, 48) and (5, 51-4) => (5, 47) and now sorting it in descending order would place them correctly and now you can simply match the pair and count it.
Note : why i used 51 only its because i just needed a bigger number for difference and since the max range of int is 50 only so i choose 51 that's all