Initially the order of problems was A-C-E-D-B. But we were not sure about last two.
This is simple straight-forward problem — you were asked to sort the teams with the following comparator: (p1 > p2) or (p1 = p2 and t1 < t2). After that you can split the teams into groups with equal results and find the group which shares the k-th place. Many coders for some reason used wrong comparator: they sorted teams with equal number of problems by descending of time. Such submits accidentally passed pretests but get WA #13.
Polygon A is convex, so it is sufficient to check only that every vertex of polygon B is strictly inside polygon A. In theory the simplest solution is building common convex hull of both polygons. You need to check that no vertex of polygon B belongs to this hull. But there is a tricky detail: if there are many points lying on the same side of convex hull than your convex hull must contain all these points as vertices. So this solution is harder to implement and has some corner case.
Another solution: cut polygon A into triangles (by vertex numbers): (1, 2, 3), (1, 3, 4), (1, 4, 5), ..., (1, n - 1, n). The sequences of angles 2 - 1 - 3, 2 - 1 - 4, 2 - 1 - 5, ..., 2 - 1 - n is increasing. It means that you can find for each vertex of B to which triangle of A it can belong using binsearch by angle.
Similarly you can cut polygon A into trapezoids (with vertical cuts). In this case you'll need a binsearch by x-coordinate.
If the initial array doesn't contain number x, than you definitely need to add it (that's +1 to answer). Than do the following. While median is strictly less than x you need to increase it. Obviously the surest way to increase the median is to add a maximal possible number (105). Similarly while the median is strictly more than x, add a number 1 to the array. Constraints are small, so you can add the numbers one by one and recalculate the median after every addition.
Also there is a solution without any cases: while the median isn't equal to x, just add one more number x to array.
Let's sort the people by decreasing of shoes size. Observe that when considering the i-th man we are interested in no more than 2 pairs of shoes: with size li and li + 1. It allows solving with dynamics. The state will be (the number of first unconsidered man i, is pair of shoes with size li available, is pair of shoes with size li + 1 available). You have 3 options: leave the i-th man without shoes or sell him a pair of shoes of one of suitable size (if available).
Obvious solution with dynamics: you need to know only how many moves are left and where is the ant. This is 4n states, each with 3 options – most of such solution passes. Observe that the vertices A, B, C are equivalent. This allows writing such solution:
int zD = 1;
int zABC = 0;
for (int i = 1; i <= n; i++) {
int nzD = zABC * 3LL % MOD;
int nzABC = (zABC * 2LL + zD) % MOD;
zD = nzD;
zABC = nzABC;
}
cout << zD;
Also this problem could be solved by log(n) with binary exponentiation of some 2 × 2 matrix into power n.










Edited -- Fixed my code! Thanks to Igel_SK!
Isn't the state for D too big?
Also, I see people doing bipartite matching in a greedy way, why does this work?
Bipartite matching with sorting shoes works correctly, it can be proofed (in russian). I think it should get TLE but the tests were weak :)
I solved with the DP this way: you have the current person and a mask that represents if the 2 sizes of shoes that this person can use are available (costumers are sorted by shoe size), so it will be a dp[10⁵][4] table.
I solved E:Tetrahedron using the problem (3^n+3*(-1)^n)/4 . Here is my solution . However it failed the system test and when I used BigInteger it passed.Here is the 2nd version. 2 question: 1.Why does the first solution fail... 2.Is there any thing I can do to avoid BigIntegers
Use
longDoubles are not accurate
Your code with long instead of double 1403711
Got the same problem.
how did you arrive at this formula can you please explain??
do the adjacency matrix A (in this problem you will have a matrix where A[i][j] = 1 if i!=j and A[i][j] = 0 if i==j). now A^2 count paths with two edges, A^3 count paths with three edges and so on, do exponentiation using diagonalization i.e A = P*D*P^(-1)
A^n = P*D^n*P^(-1)
You have to find a formula for one element on the diagonal using matrix P, D^n and P^(-1), just there you will notice the formula (3^n+3*(-1)^n)/4. (all of elements on diagonal are equal for this reason you need to find the formula of only one of them)
be carefull doing division using modulo, here you will find good information of how to do that https://codeaccepted.wordpress.com/2014/02/15/output-the-answer-modulo-109-7/
I don't understand how A^2 counts paths of length 2 and A^3 counts paths of length three etc. Am I missing some concept?
mod function in my code is not working
include <bits/stdc++.h>
using namespace std; //#define int ll; // [9,223,372,036,854,775,807 to -9.....808] 19 digits
define pb push_back
define all(x) (x).begin(),(x).end()
define mp make_pair
define vii vector < int >
define pii pair < int , int >
define vpi vector < pii >
define fi first
define se second
define mem1(a) memset(a,-1,sizeof(a))
define mem0(a) memset(a,0,sizeof(a))
define rep(i,a,b) for(int i=a;i<b;i++)
define repit(st) for(auto it=st.begin();it!=st.end();it++)
define sz(x) (int)((x).size())
define len(x) (int)((x).length())
template<typename T,typename T1>T amax(T &a,T1 b){if(b>a)a=b;return a;} template<typename T,typename T1>T amin(T &a,T1 b){if(b<a)a=b;return a;}
//const int mod=998244353; const int mod = 1000000007; const int N=1000000+6;
define M_PI 3.14159265358979323846
const int maxn=1e5+5;
int main() { ios_base::sync_with_stdio(false);cin.tie(0);cout.tie(0);
int n;cin>>n; int abc=3,d=0,abcp=3,dp=0; rep(i,2,n+1) { abc=((dp*3)%mod+(abcp*2)%mod)%mod; d=abcp; abcp=abc; dp=d; } cout<<d;}
can you plz tell me why??
What 2 x 2 matrix can be used in E? I've only seen it solved with a 4 x 4 matrix with diagonal = 0 and rest = 1.
See Egor's solution: 1390234
Can you explain the idea behind this solution?
In general, you can do matrix exponentiation (that is, raising matrix M to the N-th power) in
O(logN)time, where N is the exponent. If you exploit a "matrix notation" for your dp recurrence, then you can reduce it to this problem, thus solving it inO(logN).For example, it is possible to find the N-th fibonacci number using this method. For a better explanation, check out the "Fibonacci log N" tutorial on e-maxx.ru
let A be a matrix of 4X4 where,
A[i][j] = 1 if i != j, and 0 otherwiseNow, A represents the number of paths from i to j using 1 edge. Using some basic intuitions we can prove that A*A will represent the same but using 2 edges. So, we can A^n will represent all the paths from i to j using n number of edges. Now, you can exponent it or derive a formula. I derive a formula, see it here 51966083
Thank you for the explanation! Can you share a proof also?
Sorry about that, just ignore the post.
from math import *
def fast_exponentiation(base, n): if n == 1: return base else: if n % 2 == 0: base1 = fast_exponentiation(base, n/2)**2 return base1%1000000007 else: return (base*fast_exponentiation(base,(n-1)/2)**2)%1000000007
t = int(raw_input()) if t%2 == 0: print ((fast_exponentiation(3,t) + 3)/4)%1000000007 else: print ((fast_exponentiation(3,t) — 3)/4)%1000000007
Why is this code in Python wrong for thetraedron?
Note: you can use the built-in function
powfor fast modular exponentiation:I keep getting wrong answer...
I get right values if I put modulus outside all the expression, so:
print ((fast_exponentiation(3,t) + 3)/4)%1000000007 gives correct value, but slow and print ((fast_exponentiation(3,t) + 3)/4) within the fast exp with mod gives WA, why?
You can't divide by 4 if you use mod before it. You should multuply pow(4, p-2, p) instead
Try ((fast_exponentiation(3,t) + 3) * 250000002) % 1000000007, and take modulo on each fast_exponentiation step.
ant.ermilov thank you for the tip, I have seen it in a solution as well, but can you explain to me, or point me to somewhere that can tell me, why is that particular number used?
At first, let's try to understand, why your approach does not work. For example, we have
Y = M+1, Y % M = 1,
but (Y / 4) % M != (Y % M) / 4.
So division can be substituted by multiplication. In general, we have modulo M, divisor D and want to find such Z that for each X: (X / D) % M = ((X % M) * Z) % M.
After simple transformation we will get (X * Z) % M = 1.
For particular case 250000002 * 4 = 109 + 7 + 1.
Some extra info: Z can be found iff gcd(X, D) = 1, and simpliest way described at riadwaw's comment above. From Euler's theorem we get Z = (DM - 2) % M.
Amazing explanation! Thanks
What does non-degenerate mean in 166B - Многоугольники (Div2 B) ?
Found myself : link
@riadwaw Can you please explain In the solution to E why has nzABC been multiplied by 2 in the fifth line?
int nzABC = (zABC * 2LL + zD) % MOD;Thanks a lot.
Let Ai denote number of ways to finish near the vertex A after i moves (same for Bi, Ci, Di). Easily,
with the initial conditions
Due to the symmetry $A_i=B_i=C_i=ABC_i$, so
Nice Explanation :)
I'm interested in E,whether there is any simple formula without matrix.i can't get it,anybody got it and coubld you share it?
CAN anybody explain E in detail? Can't get it.Thanks!
Let f[A][j] is the number of ways from D to A by going j steps,as same,f[B][j], f[C][j] and f[D][j], we know f[D][0] = 1, f[A, B, C][0] = 0(because the ant starts at D).
then you get four equations below:
f[A][j] = f[B][j - 1] + f[C][j - 1] + f[D][j - 1]
f[B][j] = f[A][j - 1] + f[C][j - 1] + f[D][j - 1]
......
f[D][j] = ...
you can solve this problem in O(n),the answer is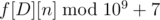 .
.
but it's too slow.you can express the four equations by matrix.then it's obvious to solve the problem by Successive Square Method with matrix in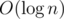 .
.
Thank you, I finally understood it!
@RAD In question B Polygons, What's the problem if we directly compute the convex hull of all points and check if any point of B is present in it ? I couldn't understand the mistake!!
I was able to solve Div 2 C Median using an O( 1 ) approach. Submission is here: https://codeforces.me/problemset/submission/166/52647089 .
Basic Idea: We have to ensure that the element we have to make as median (x) has to be at the central position. Now there can be 3 types of elements obviously: (i) smaller than x (ii) equal to x (iii) larger than x
Note that there can be duplicates so the number of elements equal to x can be more than 1 (or even 0). Our final aim is to ensure one of the elements equal to x lands up at the central position at the end. We know that in the final answer, 0 <= number of elements on right of median — number of elements on left <= 1 In case there are more than one equal elements, we can observe that the optimal answer will always have more of the extra equal elements on the side with less number of elements ( smaller or larger ). And the situation will look like this:
Now we have to find the number of elements that need to be added: Case 1: When number of smaller elements < number of larger As the left side can have one lesser elements than the right, number of elements we need to add is (elements greater than median — elements less than median — (elements equal — 1) — 1). Why elements equal — 1 ? Because one of these elements shall be at the median position. Obviously, it can't be less than 0, so we have to max it with 0. And also we subtract an additional -1 as we are allowed to have left side smaller.
Similarly we can devise Case 2 and 3 where elements on both side are qual or smaller > larger. I guess code will be able to explain itself better now !
For 166 C — Is their a direct mathematical (formula based) approach in which we dont have to use a loop once we have taken the input?
In case someone did not understand the editorial of 166E — Tetrahedron, here is a simple way of looking at the solution : zD is the number of ways of reaching D in
isteps and zABC is the number of ways of reaching A or B or C inisteps(A , B, C are equivalent points). Since the ant starts of from D, initially (ati = 0)zD = 1andzABC = 0.Now in each subsequent step, 2 things can occur :
If the ant was at D, it will come down to any of the A,B,C points. That means it has 3 options. Hence , nzABC = zD.
If the ant was at either of the A,B,C positions, it can either climb upto point D or go to any of the 2 other equivalent points i.e. if the ant was at A, it can go to D and hence nzD= 3*nzABC ; or it can go to either B or C (2 available options) which increases nzABC by 2*zABC and hence nzABC += 2*zABC.
Therefore at last
nzABC = 2*zABC + zDandnzD = 3*nzABC.I am getting TLE in problem E,i am using dp approach.Anyone please help code submission: https://codeforces.me/contest/166/submission/88417439
declear dp array globally then you will not be needed to make whole array zero .may be thats why you are getting tle
here is my code for 166E. Tetrahedron 105550054
My code is giving a time limit exceeded for the test case with n = 10000000. But when I change the vector with an array, i.e. in 105550845 It is running much faster and got accepted! Why is this problem with vectors? Why is the vector so slow? I am new here :)
this should pass
UPD: sorry I miss understood your question :)
I think it's because you're creating n unnecessary vectors while you can just creat 1
see the code above it's faster and with vectors :)
Thanks Satoru for your answer! :) I got it accepted using your correction. But still it is taking more time than with the array one. So vectors are really slow?
Yeah arrays are faster
But like a lot of people I'm not using arrays (I just use vectors) because it have benifiets more than arrays (like push_back, pop_back ... etc) and you don't need to calculate the size, just use
resizeunlike arraysHow did solutions based on Kuhn's algorithm passed in problem D? Shouldn't it get TLEd?
In problem B, how can we find the convex hull of points if there might be three or more points on the same line?
My soln for E:- Notice-its easy to notice we need total strings of length n+1 starting with d and ending with d and can have alphabets {a,b,c,d} such that no same alphabets can be consecutive. Now noting that we just need strings with a/b/c ending with a/b/c ans yeah of course no 2 same alphabets consecutive and must have length n-1. Lets denote x_n such strings with length n so if first character is a then a.......(a/b/c) now 2nd character can be b/c/d,if its d its obvious to notice we can first find such strings of length n-2 and concatenate string ad with is hence x_(n-2) strings of such type, if its b/c we can find such strings of length n-1 and argue by symmetry there will be exactly 2/3 of such strings hence 2/3*x_(n-1) hence if first charcter is a we say total=x_(n-2)+2/3*(x_(n-1)) strings and hence by symmetry again same for b and c hence total strings=>x_n=3*x_(n-2)+2*x_(n-1) this can be solved using generating functions which gives us x_n=(3*(-1)^n+(3^(n+1)))/4; we need x_n-1=(3*(-1)^n+(3^n))/4
I have another way which is more direct Combanitorics. Consider the problem of starting at an edge and landing back at same edge. No of ways for such a path = 3^n as we can go to 3 nodes from each node. Depending upon if n = odd or even we can have the ending path to be of 3 special types (DAD, DBD, DCD), and no of solutions for a node requires division by 4. This also proves how that expression is always an integer.