K-я порядковая статистика на отрезке

№	Пользователь	Рейтинг
1	tourist	4009
2	jiangly	3823
3	Benq	3738
4	Radewoosh	3633
5	jqdai0815	3620
6	orzdevinwang	3529
7	ecnerwala	3446
8	Um_nik	3396
9	ksun48	3390
10	gamegame	3386

№	Пользователь	Вклад
1	cry	164
1	maomao90	164
3	Um_nik	163
4	atcoder_official	160
5	-is-this-fft-	158
6	adamant	157
6	awoo	157
8	TheScrasse	154
8	nor	154
10	djm03178	153

Пацаны, расскажите пожалуйста, я баян придумал или нет?

Задача простая: m запросов, вывести k-ю порядковую статистику массива a[n] на отрезке [l,r].

n ≤ 10⁵, m ≤ 10⁵

Сложность: n· log(n) препроцессинг, log²(n) на запрос.

Что делаем:

1) Сортируем массив в виде пар (a_i, i), сначала по значению, потом по индексу.

2) Строим n-штук persistent segment tree, где на i-м шаге добавляем в дерево отрезков индекс элемента, который находится по i-му индексу в отсортированном массиве пар.

3) Бинпоиском находит нижнюю границу i, где в дереве отрезков i sum(l, r) ≥ k.

4) Это и есть наш ответ, выводим число.

Код: http://pastie.org/2767791

Комментарии (39)

Написать комментарий?

Malinovsky239

13 лет назад, # |

← Rev. 3 →

K-ю порядковую статистику на отрезке за O(log^2(n)) на запрос можно считать неперсистентным деревом отрезков. А при помощи персистентного можно досчить асимптотики O(log(n)) на запрос

→ Ответить

yarrr

13 лет назад, # ^ |

А как второе делать, расскажите пожалуйста.

+26

Представим, что на плоскости отмечены точки с координатами (i, a[i]). Тогда ответом на запрос будет k-я по высоте точка в вертикальной полосе, края которой соответствуют границам запроса.

Сожмём координаты и построим персистентное дерево отрезков на сумме, добавляя в позицию trans(a[i]) единицу, где trans(a) - значение а в сжатых координатах (должно получиться такое дерево, что итоговая версия будет возвращать кол-во элементов, значения которых после сжатия лежат в диапазоне от l до r). Теперь, за логарифм спускаясь из корня соответствующей версии дерева, мы умеем отвечать на запрос о k-й порядковой статистике на префиксе массива. Так как деревья отрезков для разных префиксов изоморфны, то дерево для вертикальной полосы, соответствующей отрезку запроса [L; R], можно получить, вычитая из значения в каждой вершине дерева версии R значение в соответствующей вершине версии L-1. Так как нам интересны значения только в O(log(n)) вершинах этого дерева, то не станем строить его явно, а просто будем спускаться по обеим версиям и получать нужные значения в несуществующем дереве для полосы от L до R.

P.S. Кривое вышло объяснение, но без листочка, на котором можно что-нибудь схематично изобразить, лучше не могу.

Shapo

Кто-нить знает, кто придумал такое решение впервые??? Было бы очень интересно узнать...

DimaPhil

-6

Андрей Сергеевич (andrewzta) сказал, что ему это рассказал Сережа Копелиович на петрозаводских сборах.

wistful23

Northern Subregion 2004. Problem K.
http://neerc.ifmo.ru/subregions/northern.html

Ну там O(nm) проходит, я на этих тестах как раз правильность проверял.

В 2004-ом не проходило )
По ссылке еще можно посмотреть решения жюри и участников.

_jte_

Можно за $\text{[math]}$ делать, строя дерево отрезков, в каждой вершине которого - отсорченный подмассив. Занимает $\text{[math]}$ памяти, такая задача есть и на spoj.pl.

В обсужениях этой задачи Robert Gerbitz говорил, что умеет решать за $\text{[math]}$ с препроцессом $\text{[math]}$ .

Если отсортированный подмассив в вершине получать из массивов в двух сыновьях при помощи Merge() из MergeSort'а, то препроцессинг O(N * logN) получается, как я понимаю.

Да, это опечатка была, имелось в виду за $\text{[math]}$ отвечать на запросы, препроцесс - как Вы и сказали.

yahooo

← Rev. 5 →

-9

эту задачу можно решать с помощью декартова дерева по неявному ключу, сложность: NlogN построение, и logN запрос

P.S. кст, с помощью декартова дерева, можно эту задачу даже on-line решать

P.S.S. нельзя, я ошибся, вернее все, что я написал выше-неверно

PavelKunyavskiy

Хм.. два вопроса.

1) как

2) а почему построение не за линию?

← Rev. 2 →

1) ну поступает запрос на отрезке [L;R], сплитим по L, по R, получаем три дерева: первое содержит элементы [1..L-1], второе [L;R], третье [L + 1;R], теперь второе сплитим по К, берем самую правую вершину, отвечаем на запрос и merg'им деревья

~~2) ну за линию тоже можно, просто я пишу за NlogN, за линию ни разу не писал~~

P.S. забудьте, я накосил

Если вы умеете писать дерево которое можно сплитить и по значению и по индексу, и при этом оно работает за log, то я в это не верю. Во всяком случае это некоторое yahooo-дерево, а не декартово. Хотя я могу и ошибаться.

нет, я просто как-то головой не подумал, перед тем, как писать это

Ну тогда уж до кучи это решается корневой с линией памяти и $\text{[math]}$ времени (я видимо умею еще и за $\text{[math]}$ аккуратным разбиением кусков. И мне кажется что это будет быстрее log^2 и log^3, за персистентный log не уверен. $\text{[math]}$ наверное какая-то оптимизация этого.

daftcoder

Я может туплю... А почему нам не отсортировать массив и за 1 время говорить l+k-ю статистику (просто взяв значение A[l+k])?

riadwaw

тупишь. на l,r могли быть самые мелкие числа. а могли быть самые большие к примеру. Места при сорте не сохраняются(привт, капитан)

Плохо болеть и тупить(

Элементы: 4 1 2 3

Запрос: l = 2, r = 4, k = 1.

sdya

Вообще, эта задача была этим летом на сборах в Петрозаводске в контесте команды Тавриды. При этом, были следующие ограничения: N<=450000, количество запросов <= 600000, TL 4 секунды. Вроде как ничего, кроме персистентного дерева с ответом за logN на запрос, не проходило. Авторское решение совпадает с решением из поста Malinovsky239.

MBabin

Можно же решать обычным двумерный деревом интервалов с fractional cascading, будет O(nlogn) памяти и O(logn) ответом на запрос (и думать особо не надо).

oversolver

offtop:

скажите, как решать задачу "найти количество различных чисел на отрезке"?

ACube

Знаю как в оффлайне. Отсортируем запросы по правому концу. Теперь если мы можем быстро решить задачу для какого-то префикса массива, то можно решить и исходную.

Будем двигаться от первого префикса(1..1) до N-ого(1..N). И в каком-нибудь дереве у нас единичками будут помечены лишь те элементы у которых справа нет такого-же. Ex.:

Prefix: 1 6 3 1 2 5 5 1

Signs: 0 1 1 0 1 0 1 1

Понятно что при переходе от префикса i к (i+1) убирается максимум одна пометка и добавляется одна.

Теперь чтобы решить запрос (l, r), дойдем до префикса r и найдем сумму от l до r в дереве. Сумма и есть ответ.

Если двигаться указателями то суммарная ассимптотика примерно: O(NlogN + MlogM)

ifsmirnov

Прибавляем персистенстность и получаем онлайн ответы на запросы. Задача I с ВКОШП-2010 на это была.

Nodir.Daminov

10 лет назад, # ^ |

А как решать если нужно сделать UPDATE(x,k) то есть a[x]=k ????

senitapqan

4 года назад, # ^ |

-8

можно решать с помощью merge sort tree с pbds на каждой вершине

livo8

6 месяцев назад, # ^ |

Да это реально круто

juver

Задача на SPOJ

Kasparyan_Mikhail

А почему бы не воспользоваться деревом отрезков... В каждом узле будем хранить сет с числами... А затем просто объединять сеты, а ответом будет кол-во элементов в сете... Или вместо сета хранить отсортированный массив различных чисел, а при подъеме объединять, но не добавлять повторения...

Отличная идея, но работать это будет за O(len), где len = r - l + 1.

даже хуже, будет O(nlog²n) на запрос

aangairbender

http://ejudge.upml.knu.ua/acm2014/iQmBL4zKcOmFUerSklIO/F.pdf Вот задача с приличными ограничениями (10^5) Оффлайн решение с сетами заходит. Но вот только тут граф, а в задаче выше — массив. (Хитрость: нужно меньший сет кидать в больший, иначе будет ТЛ)

Rebryk

эту задачу умею решать для всех вершин за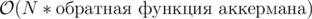 $\text{[math]}$

adamant

α(n) ведь вроде от LCA возникает?

dkorduban

9 лет назад, # ^ |

splay деревьями что ли? можно подробнее, пожалуйста?

Так это другая задача. Здесь, в отличие от начальной, все отрезки попарно либо вложены, либо не пересекаются вовсе.

вот эту задачу

Блог пользователя yarrr