I know you are tired coz of kquery's problems.I am just interested to solve this problem.without update I had on each vertex of segment tree sorted subarray,but now I can't do this with same idea (it was O(n log^2)). also is any idea which solves this problem in O(n log n) ?
→ Обратите внимание
До соревнования
Rayan Programming Contest 2024 - Selection (Codeforces Round 989, Div. 1 + Div. 2)
4 дня
Зарегистрироваться »
Rayan Programming Contest 2024 - Selection (Codeforces Round 989, Div. 1 + Div. 2)
4 дня
Зарегистрироваться »
*есть доп. регистрация
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 3993 |
| 2 | jiangly | 3743 |
| 3 | orzdevinwang | 3707 |
| 4 | Radewoosh | 3627 |
| 5 | jqdai0815 | 3620 |
| 6 | Benq | 3564 |
| 7 | Kevin114514 | 3443 |
| 8 | ksun48 | 3434 |
| 9 | Rewinding | 3397 |
| 10 | Um_nik | 3396 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 155 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 10 | nor | 152 |
→ Найти пользователя
→ Прямой эфир
↑
↓
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 26.11.2024 23:11:04 (i2).
Десктопная версия, переключиться на мобильную.
При поддержке
Списки пользователей


| Название |
|---|











Disclaimer: There's a good chance this won't quite run in time.
Divide the array into m equal-sized blocks. For each block, keep a binary indexed tree of the elements in that block. Then, for a query, you can make a single query to the BIT (to count elements less than k) for each complete block in the range, and for the two partial blocks on the end, just loop through the elements. Therefore, the query time is O(m * log(10000) + n/m). The update is just updating a single BIT = O(log(10000))
Let m = 50. Then, the total time for 200,000 queries is 200,000 * (50 * log(10000)) + 600), which is about 250 million operations.
I'm hoping there's a way to speed up the queries by slowing down the updates somehow but I can't think of any ways to do that right now.
This is a really beautiful solution!
At first, I submitted and got TLE, but after playing with the block size, I got accepted.
Here's my implementation of your great solution: C++ Code
Thanks mkirsche,nice idea to do same problems as this is,I got it ;)
Can't we use the same idea in segment tree? Each node will contain a BIT, which we can use to count elements less than k. Update is similar too.
The solution is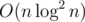 though (but it should be fast enough I guess).
though (but it should be fast enough I guess).
your idea is different,in his idea he divides array into m equal-sized blocks,and you have structore for each node of segment tree.actually,it is also possible to Build BIT, Fenwick Tree , Treap for each node in segment tree(here we can also possible to swap Treap and Segment Tree,and on each node of Treap Build this structures) complexity for each case is O(n log^2 n).
as Diguised say about 2D segment tree ,it's same as Build another segment tree on each node of segment tree and works also in log^2.
With updates you can do it in O(n log^2) if you replace sorted arrays with treaps. It is a bit complicated solution, may be it is possible to use something easier.
segment tree+treap it's so hard to implement,it's better to use mkirsche's solution in this way.
why segmenttree+treap harder than sqrtdecomposition+treap??? i thought it is the same...
for me sqrtdecomposition is much more easier than treap to implement.
Oh, sorry, i misread solution in first comment. But now i don't understand why needed BIT if there can be just array.
Don't mind, it leads again to log^2.
Can you explain how you do the update with changing only one version?! Don't you need to update all versions with index >= j (If you're updating a[j])?
Use 2D segment tree or store a persistent segment tree at each node :D.
The first time I AC this problem, I used 2D BIT, which cost so much memory (but it got AC). The main idea of this one is calculating S(x,y) which is number of elements lesser/greater than y in a[1], a[2], ... , a[x].
Later I changed to BIT and sqrt decomposition with the same idea above. You know that a 2D BIT is N 1D BITs in someway. Instead of using N 1D BITs (which is actually a 2D BIT) for N element, I used sqrt(N) 1D BITs which would be a 2D [sqrt(N) x N] BIT. That's all, the remains are just basic sqrt decomposition technique.
Complexity :
O(2*log(sqrt(N)) * log(N) + 2*sqrt(N)) = O(sqrt(N)) per query.
O(log(sqrt(N)) * log(N)) = O((log n)^2) per update operation.
...which is fast enough.
I have no idea how to solve this in O(log n) per operation/query.
your idea is good and different,but
let n=2^x
sqrt(n)=2^(x/2)
log^2 (n)=x^2
2^(x/2)=x^2
x=16,n=2^16=65536;
if n>65536 as here and in more cases it's better to write log^2(n) solution,else your solution is much faster,It help's me thanks for your explanation.
please some1 tell me how to write formulas here same us in latex?
Disregard
Hi -
recently I submit this code to this problem; except I get TLE. Solution utilizes 2D segment tree. Anyone can suggest any optimizations that will help it pass?
Thanks in advanced-
Disguised
Hi, I used a range tree of treaps and it got TLE. Code: http://codepad.org/Zy7elORD It seems that the constant factor of a treap is pretty high >_<
Has anyone been able to get AC in this problem by storing an implicit segment tree in every node of a normal segment tree? I am getting TLE using this idea.
Also how do you solve this problem by 2D segment tree or 2D BIT or by storing a BIT in each node of segment tree? Isn't that going to take too much memory?
N.B.: I have solved this problem using square root decomposition plus BIT. Theoretically the complexity of the query operation for the implicit segment tree idea should be better while that of the update operation of the sqrt idea should be better. But I am interested to know if this problem can be solved using implicit segment trees within time limit.
I got AC with it
Can you share the code?
sure. http://colorscripter.com/s/3YT074E
Thanks very much.
My O(N lg^2 N) code passes in 1.38s even though the time limit is 1sec lol. My solution: Coordinate Compression + BIT in Segment Tree.