Традиционное место для обсуждения задач :)
Расскажите, пожалуйста, A и C.
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 3993 |
| 2 | jiangly | 3743 |
| 3 | orzdevinwang | 3707 |
| 4 | Radewoosh | 3627 |
| 5 | jqdai0815 | 3620 |
| 6 | Benq | 3564 |
| 7 | Kevin114514 | 3443 |
| 8 | ksun48 | 3434 |
| 9 | Rewinding | 3397 |
| 10 | Um_nik | 3396 |
| Страны | Города | Организации | Всё → |
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 155 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 10 | nor | 152 |
Традиционное место для обсуждения задач :)
Расскажите, пожалуйста, A и C.
| Название |
|---|



A:
Когда я получил TL50 за своё решение за , я расстроился и стал засылать всякую чушь (глядя на ребят, заславших её с плюса на 14ой минуте). Зашедшей чушью оказался перебор от y-20 до y.
, я расстроился и стал засылать всякую чушь (глядя на ребят, заславших её с плюса на 14ой минуте). Зашедшей чушью оказался перебор от y-20 до y.
Хотелось бы услышать нормальное решение, да.
UPDATE: На яндексе первое решение за зашло.
зашло.
UPDATE2: Если во втором решении заменить 20 на 4, то тоже заходит.
Если это решение — бинпоиск по y с моделированием за mlogn, то в нём можно моделирование делать за O(m + n). Вместо одной очереди с приоритетами просто делаем две обычные очереди. В первую складываем отсортированный массив, на котором хотим запустить моделирование. Далее m раз достаём минимум из двух очередей и кладём (его значение + x) во вторую. Элементы в обеих очередях всегда будут идти по возрастанию, и всё работает корректно.
Первое утверждение: если наш маг получает A раз по x, а всего бонусов раздается B, то две раздачи N бонусов эквивалетны — 1 раздаем всем, каждый раз самому бедному, 2 — раздаем N- A, всем кроме первого, потом A раз нашему первому.
Отсюла условие что мы можем получить A x бонусов, (A-1)* x + начальное кол-во у первого < самый бедный ребенок из оставшихся после раздачи N-A, т.е. перед последней раздачей наш самый бедный и A бонус уходит ему.
Величина разности может быть прибавлена к ответу (min(y, (самый бедный ребенок из оставшихся после раздачи N-A) — (A-1)* x + начальное кол-во у первого), , т.е. итерируемся по раздаче, каждый раз пытаемся ему дать столько бонусов, выбираем максимум. Перед следующей итерации берем самого бедного и суем ему x конфет.
Кроме того, желающие подать апелляцию могут сделать это прямо в этом топике.
Начиная с 10-го этапа, все апелляции будут публичными. Апелляции, отправленные как-то иначе (на mail или через личное сообщение на КФ) к рассмотрению не принимаются; исключение составляют только технические вопросы, связанные с задержкой старта и так далее.
В остальном порядок рассмотрения апелляций не меняется (выбирается Апелляционное Жюри, которое и голосует по существу проблемы).
Расскажите, как решать div2 K — Barcode
Надо выеснить, какими могли быть столбики: пересматриваем их: если там есть и точки и крестики, то данные некорр.(-1), если одно из двух, то столбик назавем этим, а если только вопросики, то назавем вопросиком. Далее можем смотреть на пометки столбиков как на строку. Если в строке в подряд 2 одинаковых символа (. или Х), то это — широкий сигнал, иначе — узкий. Так как неясно что за вопросиками, то надо постепенно вычислять. Если все вопросики вычислили, то идем к ответу, иначе -1 как неоднозначнасть.
"Так как неясно что за вопросиками, то надо постепенно вычислять". Можно с этого момента подробнее.
Возможна ситуация например ".?." — можно ли определить однозначно? Если вставим точку, то будут идти 3 точки в подряд. По условию так быть неможет? Я считал, что неможет, по-этому заменял на Х. Потом есть и другие ситуации. Если невыйдет найти всех и написать, глянь на мой код: http://ideone.com/Iv8THt
А дп писал кто-то после упрощения до строки из "?.X" dp[n][a][b]. кол-во вариантов составить строку на префиксе где последний символ "a" и предпоследний символ "b"?
C: Можно просто перебрать все aj, и делители aj^2.
А как это сделать быстрее чем за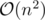 ?
?
Для каждого числа будем хранить пары чисел : первое простой делитель этого числа, и второе в какой степени этот простой делитель входить в это число. Потом с помощью рекурсии переберем все делители квадрата этого числа.
Но если взять все числа 1*2*3*5*7*11*13*17 то будет по 200 делителей, перебор делителей квадрата будет 10^4
Все числа различны же.
блин( написал решение и не отправил. спасибо.
Можно было просто запустить на макстесте и увидеть, что оно работает секунду)
забивал макс. тестом 10^6 и все числа одинаковые 10^6. Кстати, в таком случае можно решить задачу?
Можно же сжать одинаковые, и вместо единицы к ответу добавлять cnti·cntj·cntk, где i, j, k — числа, которые взяли в тройку, которые встречаются cnti, cntj, cntk раз соответственно.
Если речь идет о задаче когда нет условия отсортированности, надо учесть еще положение относительно друг друга, как я понял проблема в том, что если у нас есть числа с большим количеством делителей закинутых как-то рандомно, то непонятно что делать.
Поделитесь быстрым рекурсивным перебором. Вот такой работает на яндексе 1.327s. Упихать это в одну секунду на ejudge у меня не получается.
Вот такой получает АС
Спасибо. Упорядочивание простых множителей в факторизации по убванию приносит дополнительные ~100 миллисекунд ускорения. Однако, запихить в одну секунду таймлимита в еджадже по-прежнему не удаётся.
Видимо, во втором дивизионе сдать эту идею было нереально.
У меня еще предпосчет простых делителей числа.
Это не сильно помогает, так как предподсчёт равносилен худшему случаю.
0.6 на Яндексе, OK на ejudge
Спасибо за эффективный алгоритм факторизации. ~500 мс ускорения на яндексе. Эджаджу этого не хватило, пришлось ещё скопировать иф с 97 строчки.
Итоговый код
Насчёт алгоритма: если я правильно понимаю, массив
dpпризван избавить от операций деления. Однако на деле, конкретно в этой задаче, у меня получилось примерно одинаковое время с ним и с делением.Научите меня заходить через яндекс на опенкап. Я не смог найти точку входа.
http://www.opencup.ru/ -> Enter Sponsor Contest
Там попросит логин с паролем. От еджаджа должен подходить.
Простое и очевидное решение — давайте пресдставим a[i] как x * x * y, где x — максимально возможное, тогда a[k] должно быть равно y * z * z, где z > x, в таком случае будет существовать корень из их произведения sqrt(x * x * y * y * z * z) = x * y * z = a[j] Отсюда само решение — решето для раскладывания чисел, потом пробегаемся по первому, дальше пробегаемся по возможным z, смотрим если все три числа у нас есть во множестве, плюсуем ответ
Можно перебрать все пары ai, aj, их мало: aj^2 делится на ai, поэтому перебираем ai, а для них — aj решетообразным процессом.
A:
Выкинем первого бобо, промоделируем все m операций. Пусть i-ая операция — это прибавление x конфет к j-ому бобо, и перед этой операцией у него было b конфет. Тогда попробуем прибавить к первому бобо b - a1 конфет. При этом все операции, проделанные до i-ой не изменятся, а после i-ой каждый раз, когда мы будем давать конфеты j-ому бобо, нужно будет перед этим дать конфеты первому бобо. Бинпоиском можно найти, сколько конфет мы дадим первому бобо после i-ой операции. Ещё нужно отдельно разобрать случаи, когда мы даём все y конфет и когда мы ничего не даём.
Есть аналогичное и полностью линейное решение. Нужно лишь пользоваться фактом, что если мы хотим сравнять первого пацана с каким-то другим пацаном, нужно делать это как можно позже. А если выписать для каждого пацана номера ходов, на которых происходило добавление к его кучке конфет, можно однозначно восстановить номера позиций первого пацана, если бы он был приравнен к выбранному. Получается, что за количество прибавлений к выбранному пацану мы узнаем, сколько прибавлений произошло бы к первому — сумма всех этих количеств равна m.
По F: сначала удаляем все листья (листом будет называться вершина, из которой нельзя уйти хотя бы в одну из двух сторон). Всё что останется — точно образует цикл. Переворачиваем самую дешевую палку и вновь удаляем листья, потом еще раз и еще пока граф не опустеет. Вердикт: Wrong Answer 16. Подскажите правильное решение.
Нужно найти максимальный остов.
Легко доказать, что повернув палку, которая в цикле, мы не образуем новый цикл. Следовательно нужно выкинуть некоторые ребра с макс весом -> макс. остов.
расскажите кто-нть В пожалуйста
Считаем по magic столбцов и строк по краям, дальше всё вырождается в win[i][j] = win[i — 1][j — 1]
легко доказать, что magic = 2
да, но написать magic = 228 и заслать, не думая легче...
У нас меньше 4 не заходило, странно. Для 4 я доказал и зашло.
Мы доказали для 2 строк, но для всех корме диагонали, для диагонали делали один шаг напрямую
Можно заметить, что если x < y и 3 ≤ x, то ответ для (x, y) равен ответу для (x - 1, y - 1). Аналогично для x > y
Расскажите пожалуйста A, C И J
J — перебираем биты от старших к младшим. Если чисел с данным битом нечётное число, то мы обязаны взять его в ответ. Иначе поддерживаем множество позиций, где можно ставить перегородки так, чтобы слева и справа было чётное число чисел с заданным битом. Пересекаем множества перегородок по всем битам, которые можно не брать в ответ. Код
J: перебираем биты в ответе с самого старшего. Смотрим в скольких числах этот бит есть, если их количество нечетное, то мы ничего не сможем сделать, в ответе этот бит в любом случае будет. Если же количество этого бита в числах четное — то мы можем убрать его из ответа, если объединим в одну группу первое и второе число (а так же все числа между ними), где встречается этот бит. Аналогично объединяем 3 и 4, 5 и 6 и т.д. Если в итоге у нас получилось меньше, чем m групп, то так объединить числа не получится, а значит и убрать этот бит из ответа. Если же групп не менее m, то можем заменить исходный набор данных и продолжить перебирать биты ответа. Код
Спасибо
Расскажите G, H и I :)
H:
Найдем центр дерева и подвесим дерево за него. Постараемся разбить его поддеревья на две примерно равные половины. Теперь найдем расстояния от корня до всех вершин. В одной половине дерева поставим первую координату вектора - dist, в другой — + dist. Далее запустимся рекурсивно от половинок. При сливании ответов нужно не забыть отнормировать координаты так, чтобы в вершине они совпали.
Поймём, что мы получили валидный ответ. Рассмотрим пару вершин. Максимальная по модулю координата их разности — это та, которую мы поставили в тот момент, когда отнесли две эти вершины в разные половинки. А разность этих координат — это как раз расстояние между этими вершинами.
Теперь почему координат не очень много. Тут не совсем понятно. Если бы мы делили каждый раз пополам, то было бы не больше log21000 = 10 координат. Но мы делим хуже. Точно правда, что координат не больше log3 / 21000 = 17. Но, может быть, плохого теста не существует.
По G ничего не пишут, расскажу то, что мы придумали. На контесте WA 23, в дорешке TL 63.
Дисклеймер: Возможно, это решение неправильное/долгое. А может просто у нас руки кривые :)
Совсем глобально: будем искать MST Краскалом. Что у нас при этом происходит — склеиваются компоненты. Дак вот, будем для набора вершин хранить вероятность того, что такой набор вершин в ходе Краскала был компонентой связности, а также мат.ожидание веса этой самой компоненты.
Менее глобально: дп по маскам вершин. Состояние — вероятность события и мат.ожидание, помноженное на эту вероятность.
Теперь интересный момент: хранить эту штуку мы будем как функцию от некоторого x, где x — ограничение сверху на вес ребёр, входящих в MST на этих вершинках. Утверждается, что эта функция — это многочлен.
Тогда ответ — это значение ans[2n - 1] в точке x = 1.
Теперь как делать переход. Зафиксировали мы текущую маску вершин. Переберем, какие две подмаски вершин только что склеились (в нас). Этим мы заодно зафиксируем k — кол-во ребёр между этими двумя подмасками.
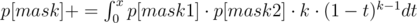
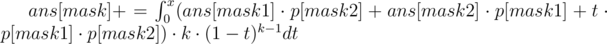
t — это вес ребра, которое мы только что добавили. Тогда все рёбра, которые уже были в компонентах, должны быть меньшего веса.
Из переходов также видно, что это действительно многочлены.
Я придумал такое, но это даёт WA24:
f[G](x) -- матожидание веса минимального остовного дерева графа G, если известно, что минимальное ребро в графе (а значит в MST) равно x.
Тогда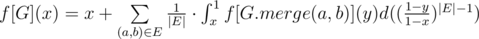 .
.
Чтобы считать всё в многочленах будем хранить (1 - x)|E| - 1·f[G](x).
Достижимых графов не более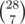
Я так понимаю, раз мы вырезаем минимальное ребро, то мы разбиваем граф на компоненты. Тогда как понять, на какие именно компоненты?
Просто ищем остов для графа с объединёнными концами ребра, которое мы только что взяли. То есть какими бы ни были остальные рёбра, наше всегда войдёт в MST, потому есть априорное знание, что оно минимального веса.
Ну тогда это странно. Возьмем любой миностов, который мы построили. В нем любое ребро минимального веса. Просто потому что мы добавляем ребро только если оно минимального веса.
========================================================
Не очень понял, попробую ещё раз рассказать, что я делаю:
Мне сказали, что минимальное ребро имеет вес в точности x.
Перебираю, какое это будет ребро, каждое с вероятностью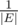 .
.
Потом перебираю какой вес будет у минимального ребра в графе, который получен из текущего объединением 2х вершин (это y, который больше либо равен x).
Вероятность, что все остальные рёбра имеют вес не меньший y это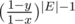 (что они не меньше x мы уже знаем).
(что они не меньше x мы уже знаем).
Тогда при зафиксированном y нужно домножать на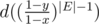 .
.
Теперь понял.
А d — это дифференциал? Почему не просто на эту вероятность а потом на dy?
=====================================================
Да, дифференциал.
Эта вероятность -- вероятность того, что вес следующего по минимальности ребра будет в отрезке [y, 1]. Если просто домножить на эту вероятность, то получится что-то странное.
Можно представить, что y перебираем дискретно, тогда при "фиксированном" y нужно домножать на p(y ≤ y') - p((y + Δ y) ≤ y').
Нашёл баг -- переполнение
long long. Нужны дроби с длинной арифметикой. Печально.А решение действительно бывает в
4139состояниях.Опишу общие идеи G и I без особых подробностей.
G: Для начала: матожидание k-й порядковой статистики из m равномерно распределенных независимых случайных величин из отрезка [0, 1] равно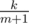 . По линейности матожидания получаем, что ответ это
. По линейности матожидания получаем, что ответ это 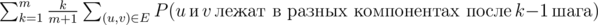 . Искомую вероятность для всех ребер можно посчитать динамикой: состоянием будет разбиение графа на компоненты связности (их не более 4140). Пересчет динамики для разбиения происходит через меньшие разбиения. Итого решение за O(mK), где K — количество переходов в динамике.
. Искомую вероятность для всех ребер можно посчитать динамикой: состоянием будет разбиение графа на компоненты связности (их не более 4140). Пересчет динамики для разбиения происходит через меньшие разбиения. Итого решение за O(mK), где K — количество переходов в динамике.
I: Заменим все красные ребра на ребра с весом 0, все зеленые ребра на ребра с весом 1, все синие на ребра с весом n. Теперь вес остовного дерева однозначно определяет, сколько в нем ребер каждого цвета. Свели задачу к следующей: нужно для всех чисел от 0 до (n - 1)n сказать, сколько в графе остовных деревьев с таким весом. Используя обобщенную теорему Кирхгоффа, составим производящую функцию для такой последовательности (про это, например, здесь). После этого надо вычислить эту функцию в n2 точках и восстановить коэффициенты полинома по значениям. Итоговое время: O(n3)·O(n2) + O(n4) = O(n5) (n2 раз вычисляем определитель матрицы размера n и за O(n4) восстанавливаем коэффициенты по значениям).
Как решается Е?
+
В E надо ускорить стандартную квадратную динамику f(i, a) — количество правильных ответов среди первых i вопросов, если ответов А было ровно a штук.
Напишем переход такой динамики в случаи если i-ый вопрос был про кол-во вариантов ответа А сделанных ранее и варианты ответа — xi, yi:
f(i, A) = min(f(i - 1, A - 1) + (xi = = A - 1), f(i - 1, A) + (yi = = A))
Аналогично для вопросов про вариант B.
Можно нарисовать квадратную таблицу и обозначить переходы динамики стрелками с весом 1 или 0. При этом кол-во стрелок с 1 весом в каждой строке будет не более 2. Теперь можно переформулировать задачу — найти путь от верхнего левого угла таблицы в любую нижнюю точку, который проходит по максимальному числу стрелок с весом 1. Такую задачу можно решить за O(mlog(m)), где m это количество стрелок веса 1, используя какую-то СД.
Расскажите еще D пожалуйста
Сожмём все позиции, где стоят одинаковые символы в компоненты. Между компонентами есть рёбра, обозначающие, что у соответствующих вершин разный цвет.
Теперь делаем следующее: в каждую вершину запишем число c, берём вершину максимальной степени, домножаем ответ на число, записанное в ней, делаем - 1 всем соседям, удаляем вершину.
Два вопроса:
1) Каждому 0 мы ставим отдельную компоненту, так?
2) Какая интуиция стоит за тем, что нужно брать компоненту с наибольшей степенью? Ну то есть не очень понятно, почему если делать именно так, ответ посчитается корректно
UPD Уже обьяснили ниже, спасибо.
Если промоделировать вычисление префикс-функции, мы получим множество пар индексов (i, j), таких что si = sj, или si ≠ sj. Равные символы сразу объединяем в компоненты, которые сжимаем до вершин и получаем граф, где ребра проведены между вершинами с разными буквами. Этот граф нужно покрасить в c цветов. В нем будет вершина (первый символ) соединенная со всеми остальными. Ее можно удалить, тогда граф распадется на компоненты, в каждой из которых также будет вершина соединенная со всеми, и тд. В коде это будет выглядеть как сортировка вершин по количеству ребер и следующий проход по ним:
О, вроде все понятно, спасибо.
Есть еще такое решение:
Будем сами делать КМП. Если pi[idx] ≠ 0, то символ idx равен какому-то из предыдущих, а значит однозначно определен. Значит на ответ влияют только те символы, у которых pi[idx] = 0.
Выпишем теперь список всех символов, которые мы пройдем в ходе КМП для idx. idx должен быть неравен каждому из них. Проблема в том, что они-то могут быть равны друг другу. Но заметим, что когда мы считали КМП для каждого числа из списка, мы тоже шли по этому списку (до того, как воткнулись в символ, равный нашему). Зафиксируем некоторый символ c и посмотрим на все позиции из списка, в которых записан c. Несложно понять, что единственная из них с нулевым значением префикс-функции — это самая маленькая.
Таким образом, кол-во символов, запрещенных для позиции idx равно кол-ву пройденных позиций с нулевым значением префикс-функции.