A. В этой задаче нужно было просто сделать то, что требуется в условии. А именно - последовательно считать слова. Для каждого слова определить длину L, его первую и последнюю буквы. Если длина слова не больше 10 - вывести слово без изменений, иначе - вывести первую букву, затем L - 2, а затем последнюю букву.
B. Сначала найдем величину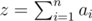 . Она равна ⌊ mnk / 100⌋, где ⌊ x⌋ - операция округления вниз. После этого первые ⌊ z / k⌋ квадратиков заполняем полностью, (⌊ z / k⌋ + 1)-ый квадратик (если он существует) заполняем на z - ⌊ z / k⌋ k, а у оставшихся квадратиков оставляем насыщенность 0.
. Она равна ⌊ mnk / 100⌋, где ⌊ x⌋ - операция округления вниз. После этого первые ⌊ z / k⌋ квадратиков заполняем полностью, (⌊ z / k⌋ + 1)-ый квадратик (если он существует) заполняем на z - ⌊ z / k⌋ k, а у оставшихся квадратиков оставляем насыщенность 0.
C. Назовем правильный многоугольник, во всех вершинах которого сидят счастливые рыцари, хорошим. Сторону правильного многоугольника будем измерять в количествах дуг, на которые рыцари делят границу круглого стола.
Зафиксируем длину стороны - пусть она будет длины k. Заметим, что правильным многоугольник с такой длиной стороны существует только тогда, когда k делит n. Всего таких многоугольников ровно k штук, а каждый из них имеет ровно n / k вершин. Будет проверять каждый из этих многоугольников на хорошесть просмотром всех его вершин - просто посчитаем количество счастливых рыцарей в вершинах и, если это количество равно n / k, то многоугольник хороший. Проверка всех многоугольников с фиксированной длиной стороны занимает O(n) времени.
Теперь заметим, что n имеет порядка делителей. Действительно, все делители (может быть, кроме одного) можно разбить на пары (для i будет соответствовать n / i, для i = n / i пары нет). Ровно один из делителей в паре будет меньше, чем
делителей. Действительно, все делители (может быть, кроме одного) можно разбить на пары (для i будет соответствовать n / i, для i = n / i пары нет). Ровно один из делителей в паре будет меньше, чем  . Это означает, что количество пар не превосходит
. Это означает, что количество пар не превосходит  , а число делителей не превосходит
, а число делителей не превосходит 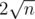 .
.
Отсюда вытекает решение - переберем все делители n и для каждого из них проверим существование хорошего многоугольника со стороной, равной этому делителю. Итого сложность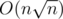 .
.
На самом деле при достаточно больших n имеет место оценка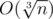 делителей. Тогда сложность решения уменьшается до O(n4 / 3). Впрочем, n = 105 не такое уж и большое - максимальное число делителей для чисел не больше 105 равно 128.
делителей. Тогда сложность решения уменьшается до O(n4 / 3). Впрочем, n = 105 не такое уж и большое - максимальное число делителей для чисел не больше 105 равно 128.
Возможные ошибки в данной задаче могли быть вызваны тем, что рассматривались "многоугольники" с одной и двумя вершинами.
UPD. Участниками также было найдено решение, работающее за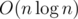 . Это решение основано на идее, что если имеется хороший многоугольник на xy вершин, то имеется и хороший многоугольник на x вершин. Поэтому нужно было лишь проверить простые делители n (за исключением 2 - вместо нее нужно было рассматривать 4).
. Это решение основано на идее, что если имеется хороший многоугольник на xy вершин, то имеется и хороший многоугольник на x вершин. Поэтому нужно было лишь проверить простые делители n (за исключением 2 - вместо нее нужно было рассматривать 4).
D. Данную задачу нужно было аккуратно разбить на подзадачи, а затем каждую из них аккуратно закодить.
Авторское решение подразумевает следующие подзадачи:
1. Проверить квадрат 3 × 3 на валидность. А именно - все в нем все карты имеют одинаковую масть или расличные достоинтсва. На самом деле из того, что у 9 карт одинаковые масти, следует что они разных достоинств. Поэтому можно было проверить только то, что достоинства различны.
2. Найти 2 валидных не пересекающихся квадрата 3 × 3 или сообщить, что таких нет. Для этого нужно аккуратно перебрать все пары квадратов и проверить их пересечение. Если они не пересекаются - с помощью подзадачи 1 проверить их валидность и, в случае удачи, возвратить это два квадрата.
3. Определить множесто карт, на которые можно заменить джокеров. Нужно было сгенерировать всю колоду без джокоров и для каждой карты проверить находится ли она в прямоугольнике n × m. Если нет - добавить ее в искомое множество.
4. Определить количество джокеров и определить их месторасположение.
5. Общая задача. Решим сначала подзадачи 3 и 4. Теперь, в зависимости от количество джокеров, будем подставлять туда, где они находятся, 0, 1 или 2 карты из множества, полученного из подзадачи 3. После каждой подстановки будем решать подзадачу 2. После всех вариантов подстановок аккуратно выводим ответ.
Решение имеет сложность O(n2m2) с небольшой константой.
E. Сначала надо было использовать поисковик, найти таблицу Менделеева в каком нибудь печатном виде, сделать copy-paste (один или несколько) и аккуратно отформатировать, удалив лишнее. Это механическая работа, занимающая не более 5 минут времени. Также можно было написать парсер, переделывающий таблицу в нужный вид. Следует отметить, что авторское решение не подразумевает перепечатку руками 100 констант с картинки. Далее нужно построить два ассоциативных массива число->символ и символ->число (или просто в лоб реализовать процедуры, переводящие одно в другое и обратно).
Итак, у нас есть набор чисел, некоторые из которых нужно сложить так, чтобы получить другой набор чисел. Воспользуется динамеческим программированием на подмножествах.
Сначала посчитаем динамику dp1[маска]->сумма. А именно, для каждого подмножества из начального набора найдем сумма нормеров атомов в этом подмножества. Это динамика легко считается за O(2nn).
Теперь будем считать вторую динамику dp2[маска]->число. Число означает длину префикса конечной последовательности атомов, которую мы можем получить из данного подмножества путем слияния некоторых атомов. Число равно -1, если получить данный префикс невозможно.
Вторую динамику можно пересчитать за O(3n). А именно - идем по маскам, если dp2[маска]!=-1, то пребираем все подмножества из оставшихся атомов (инвертируем текущую маска и берем все ее подмаски).
Если из какого то подмножества можно сделать (dp2[маска]+1)-ый атом из конечного набора (это проверяется за O(1) для каждой маски брагодаря dp1), то пересчитываем dp2[маска XOR подмаска]=dp2[маска]+1.
В конце, если dp2[2n - 1]=k, то решение есть. Если вместе с динамикой dp2 хранить маску подмножества атомов, из которых мы получаем послежний атом в префиксе, то в конце несложно восстановить ответ. Если dp2[2n - 1]!=k, то решения нет.
Сложность решения O(3n + 2nn).
В данной задаче так же проходили различные переборы с отсечениями - для таких решений очень сложно придумать контртесты.
UPD. SkorKNURE нашел решение за O(2nn). По сути это следующая модификация авторского решения:
Вместо dp2 будем считать динамику dp2'[маска]->(i,j), где i - длина префикса, который покрывает маска, а j - часть номера (i+1)-го атома, которую покрывает маска.
Теперь мы идем по всем маскам. Переход выполняется за O(n) - мы перебираем все нули текущей маски (атомы, которые еще ничего не покрывают) и пытаемся каждым "нулем" покрыть остаток номера (i+1)-го атома результирующего набора. Пусть номер атома для текущего "нуля" p, а сам атом q-ый по счету в начальном наборе. Если мы после дабавления этого нуля все равно не покрываем (i+1)-ый атом, то срабатывает переход dp2'[маска XOR (1<<q)]=(i,j+p). Если мы покрываем нулем атом полностью (но не перекрываем!, т.е. если p строго равен остатку номера (i+1)-го атома), то срабатывает переход dp2'[маска XOR (1<<q)]=(i+1,0).
Динамика dp1 остается не нужна. Если в итоге dp2'[2n - 1]=(k,0), то решение найдено (и его несложно восстановить). Иначе решения нет. Сложность, очевидно, O(2nn).
B. Сначала найдем величину
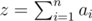 . Она равна ⌊ mnk / 100⌋, где ⌊ x⌋ - операция округления вниз. После этого первые ⌊ z / k⌋ квадратиков заполняем полностью, (⌊ z / k⌋ + 1)-ый квадратик (если он существует) заполняем на z - ⌊ z / k⌋ k, а у оставшихся квадратиков оставляем насыщенность 0.
. Она равна ⌊ mnk / 100⌋, где ⌊ x⌋ - операция округления вниз. После этого первые ⌊ z / k⌋ квадратиков заполняем полностью, (⌊ z / k⌋ + 1)-ый квадратик (если он существует) заполняем на z - ⌊ z / k⌋ k, а у оставшихся квадратиков оставляем насыщенность 0.C. Назовем правильный многоугольник, во всех вершинах которого сидят счастливые рыцари, хорошим. Сторону правильного многоугольника будем измерять в количествах дуг, на которые рыцари делят границу круглого стола.
Зафиксируем длину стороны - пусть она будет длины k. Заметим, что правильным многоугольник с такой длиной стороны существует только тогда, когда k делит n. Всего таких многоугольников ровно k штук, а каждый из них имеет ровно n / k вершин. Будет проверять каждый из этих многоугольников на хорошесть просмотром всех его вершин - просто посчитаем количество счастливых рыцарей в вершинах и, если это количество равно n / k, то многоугольник хороший. Проверка всех многоугольников с фиксированной длиной стороны занимает O(n) времени.
Теперь заметим, что n имеет порядка
 делителей. Действительно, все делители (может быть, кроме одного) можно разбить на пары (для i будет соответствовать n / i, для i = n / i пары нет). Ровно один из делителей в паре будет меньше, чем
делителей. Действительно, все делители (может быть, кроме одного) можно разбить на пары (для i будет соответствовать n / i, для i = n / i пары нет). Ровно один из делителей в паре будет меньше, чем  . Это означает, что количество пар не превосходит
. Это означает, что количество пар не превосходит  , а число делителей не превосходит
, а число делителей не превосходит 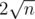 .
.Отсюда вытекает решение - переберем все делители n и для каждого из них проверим существование хорошего многоугольника со стороной, равной этому делителю. Итого сложность
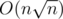 .
.На самом деле при достаточно больших n имеет место оценка
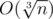 делителей. Тогда сложность решения уменьшается до O(n4 / 3). Впрочем, n = 105 не такое уж и большое - максимальное число делителей для чисел не больше 105 равно 128.
делителей. Тогда сложность решения уменьшается до O(n4 / 3). Впрочем, n = 105 не такое уж и большое - максимальное число делителей для чисел не больше 105 равно 128.Возможные ошибки в данной задаче могли быть вызваны тем, что рассматривались "многоугольники" с одной и двумя вершинами.
UPD. Участниками также было найдено решение, работающее за
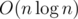 . Это решение основано на идее, что если имеется хороший многоугольник на xy вершин, то имеется и хороший многоугольник на x вершин. Поэтому нужно было лишь проверить простые делители n (за исключением 2 - вместо нее нужно было рассматривать 4).
. Это решение основано на идее, что если имеется хороший многоугольник на xy вершин, то имеется и хороший многоугольник на x вершин. Поэтому нужно было лишь проверить простые делители n (за исключением 2 - вместо нее нужно было рассматривать 4).D. Данную задачу нужно было аккуратно разбить на подзадачи, а затем каждую из них аккуратно закодить.
Авторское решение подразумевает следующие подзадачи:
1. Проверить квадрат 3 × 3 на валидность. А именно - все в нем все карты имеют одинаковую масть или расличные достоинтсва. На самом деле из того, что у 9 карт одинаковые масти, следует что они разных достоинств. Поэтому можно было проверить только то, что достоинства различны.
2. Найти 2 валидных не пересекающихся квадрата 3 × 3 или сообщить, что таких нет. Для этого нужно аккуратно перебрать все пары квадратов и проверить их пересечение. Если они не пересекаются - с помощью подзадачи 1 проверить их валидность и, в случае удачи, возвратить это два квадрата.
3. Определить множесто карт, на которые можно заменить джокеров. Нужно было сгенерировать всю колоду без джокоров и для каждой карты проверить находится ли она в прямоугольнике n × m. Если нет - добавить ее в искомое множество.
4. Определить количество джокеров и определить их месторасположение.
5. Общая задача. Решим сначала подзадачи 3 и 4. Теперь, в зависимости от количество джокеров, будем подставлять туда, где они находятся, 0, 1 или 2 карты из множества, полученного из подзадачи 3. После каждой подстановки будем решать подзадачу 2. После всех вариантов подстановок аккуратно выводим ответ.
Решение имеет сложность O(n2m2) с небольшой константой.
E. Сначала надо было использовать поисковик, найти таблицу Менделеева в каком нибудь печатном виде, сделать copy-paste (один или несколько) и аккуратно отформатировать, удалив лишнее. Это механическая работа, занимающая не более 5 минут времени. Также можно было написать парсер, переделывающий таблицу в нужный вид. Следует отметить, что авторское решение не подразумевает перепечатку руками 100 констант с картинки. Далее нужно построить два ассоциативных массива число->символ и символ->число (или просто в лоб реализовать процедуры, переводящие одно в другое и обратно).
Итак, у нас есть набор чисел, некоторые из которых нужно сложить так, чтобы получить другой набор чисел. Воспользуется динамеческим программированием на подмножествах.
Сначала посчитаем динамику dp1[маска]->сумма. А именно, для каждого подмножества из начального набора найдем сумма нормеров атомов в этом подмножества. Это динамика легко считается за O(2nn).
Теперь будем считать вторую динамику dp2[маска]->число. Число означает длину префикса конечной последовательности атомов, которую мы можем получить из данного подмножества путем слияния некоторых атомов. Число равно -1, если получить данный префикс невозможно.
Вторую динамику можно пересчитать за O(3n). А именно - идем по маскам, если dp2[маска]!=-1, то пребираем все подмножества из оставшихся атомов (инвертируем текущую маска и берем все ее подмаски).
Если из какого то подмножества можно сделать (dp2[маска]+1)-ый атом из конечного набора (это проверяется за O(1) для каждой маски брагодаря dp1), то пересчитываем dp2[маска XOR подмаска]=dp2[маска]+1.
В конце, если dp2[2n - 1]=k, то решение есть. Если вместе с динамикой dp2 хранить маску подмножества атомов, из которых мы получаем послежний атом в префиксе, то в конце несложно восстановить ответ. Если dp2[2n - 1]!=k, то решения нет.
Сложность решения O(3n + 2nn).
В данной задаче так же проходили различные переборы с отсечениями - для таких решений очень сложно придумать контртесты.
UPD. SkorKNURE нашел решение за O(2nn). По сути это следующая модификация авторского решения:
Вместо dp2 будем считать динамику dp2'[маска]->(i,j), где i - длина префикса, который покрывает маска, а j - часть номера (i+1)-го атома, которую покрывает маска.
Теперь мы идем по всем маскам. Переход выполняется за O(n) - мы перебираем все нули текущей маски (атомы, которые еще ничего не покрывают) и пытаемся каждым "нулем" покрыть остаток номера (i+1)-го атома результирующего набора. Пусть номер атома для текущего "нуля" p, а сам атом q-ый по счету в начальном наборе. Если мы после дабавления этого нуля все равно не покрываем (i+1)-ый атом, то срабатывает переход dp2'[маска XOR (1<<q)]=(i,j+p). Если мы покрываем нулем атом полностью (но не перекрываем!, т.е. если p строго равен остатку номера (i+1)-го атома), то срабатывает переход dp2'[маска XOR (1<<q)]=(i+1,0).
Динамика dp1 остается не нужна. Если в итоге dp2'[2n - 1]=(k,0), то решение найдено (и его несложно восстановить). Иначе решения нет. Сложность, очевидно, O(2nn).











*LOL*
(I feel proud of myself for this guess :))
расличные -> различные
найдем сумма -> найдем сумму
текущую маска -> текущую маску
послежний -> последний
так же проходили -> также проходили
For (C) it suffices to check polygons with a prime number of sides (except for 2, then check 4), that gives O(log n) divisors to check.
does dp1 calculation really need dynamic programming?
I think, this part can be done by simple 2 loops.
dp1[mask]=0;
for(int i=0;i<n;i++){
if(mask&(1<<i)) dp1[mask]+=(weight of i-th atom);
}
}
(Yes, I'm a necroposter)
Me too apparently
Why do I need to output $$$L - 2$$$?
see input vs output.. for less than 11 charactered string we print the string back but for string greater than 10 characters we print first char last char and length of string if those two chars weren't there