A. In this problem you can just do what is written in the statement. Let read all words. For each of them compute its length L, its the first and the last letter. If L > 10, output word without any changes, otherwise output the first letter, next L - 2 and finally the last letter.
B. At first, compute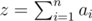 . It equals ⌊ mnk / 100⌋, where ⌊ x⌋ is rounding down. Next we fill first ⌊ z / k⌋ squares with a saturation k. (⌊ z / k⌋ + 1)-th square (if it exists) we fill in a saturation z - ⌊ z / k⌋ k. All other squares we leave with a saturation 0.
. It equals ⌊ mnk / 100⌋, where ⌊ x⌋ is rounding down. Next we fill first ⌊ z / k⌋ squares with a saturation k. (⌊ z / k⌋ + 1)-th square (if it exists) we fill in a saturation z - ⌊ z / k⌋ k. All other squares we leave with a saturation 0.
C. Define an good polygon as a regular polygon which has a knight in a good mood in every of its vertex. Side of polygon we will measure in arcs which is obtained by dividing border of round table with knights.
Freeze the length of the side. Let this length equals k. Observe that the regular polygon with such length of side exists only if k divides n. We have exactly k of such polygons. Every of them has exactly n / k vertices. Check every of the polygons for goodness by review all of its vertices.
If sum of vertices with knight in a good mood equals to n / k, this polygon is good. Checking of all polygons with some frozen length of side works in an O(n).
Now observe that n has of divisors. Really, all divisors (may be except only one) we can divide into pairs (for i corresponds n / i, for i = n / i there is no pair). One of divisors in every pair less than
of divisors. Really, all divisors (may be except only one) we can divide into pairs (for i corresponds n / i, for i = n / i there is no pair). One of divisors in every pair less than  . It means thah number of pairs no more than
. It means thah number of pairs no more than  and number of divisors no more than
and number of divisors no more than 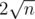 .
.
It gives solution - iterate over all divisors of n and for every of them check existence of good polygon with length side equals this divisor. Solution has an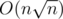 time.
time.
In reality for big n is has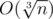 divisors. So solution actually has O(n4 / 3)-complexity. For all numbers less than 105 maximal number of divisors is 128.
divisors. So solution actually has O(n4 / 3)-complexity. For all numbers less than 105 maximal number of divisors is 128.
UPD. There was found an solution by some participants. This solution uses following idea. If we have a good polygon with xy vertices, we also have a good polygon with x vertices. So we can check only prime divisors of n (except 2 - here we must check 4).
solution by some participants. This solution uses following idea. If we have a good polygon with xy vertices, we also have a good polygon with x vertices. So we can check only prime divisors of n (except 2 - here we must check 4).
D. This problem can be divided into some subproblems.
Author's solution means following ones:
1. Check validness of square 3 × 3. Square is valid if all cards in it has equal suit or different rank. You may not check equal suit because equal suits imply different ranks.
2. Find 2 valid noninetsect squares 3 × 3 or return thah there are no ones. You can check all pairs of squares for inetsection. If some pair has no intersections check them with solution of subproblem 1.
3. Build set of cards which can be replaced with jokers. Generate full deck without jokers and drop from it all cards which in rectangle n × m are present.
4. Find number of jokers and its positions in rectangle.
5. Main subproblem. At first, solve subproblems 3 and 4. Now replace jokers in rectangle with cards from deck from subproblem 3 by all possible ways. For every replace solve subproblem 2. Arter all of variants of replacement just output answer.
There are O(n2m2) solution with small constant.
E. At first, you can use some search engine for find periodic table in some printable form. Next use copy-paste (one or several times) and format it by deleting all excess. It is mechanical work for no more than 5 minutes. Also some parser may be written. Note than author's solution does not mean write 100 symbols by hand from a picture. Next build some functions which transform symbols into numbers and vice versa.
So, we have some set of numbers. We need summarize some from them and get some another set of numbers. We will use dymanic programming over subsets.
Compute the first dp dp1[mask]->sum. For each subset calculate sum of numbers of all atoms in this subset. It can be done in O(2nn).
Now compute the second dp dp2[mask]->length. The "length" is a length of some prefix of result sequence of atoms which can be obtained by subset mask. If length -1, it means that it is impossible to get any prefix from this subset.
The second dp we can calculate in O(3n). Iterate over all masks and if dp2[mask]!=-1, iterate all its subsets of remained atoms (invert mask and get all its submasks). If some subset has sum of numbers which equals number of (dp2[маска]+1)-th atom from result set, recalculate dp2[mask XOR submask]=dp2[mask]+1.
At end, if dp2[2n - 1]=k, there are solution.
There are O(3n + 2nn) solution.
In this problem some brutforce solutions are passed because it is difficult to pick up some counterexample.
UPD. SkorKNURE found a solution in O(2nn). This solution is some modification of the author's solution.
Instead of dp2 calculate dp dp2'[mask]->(i,j), where i is a length of prefix which mask covers and j is part of number of (i+1)-th atom which mask covers.
Iterate over all masks. For each mask iterate over all its 0-bits (they are atoms which cover nothing from the finish set). We try to cover with this 0-bit a remainder of number of the (i+1)-th atom from the finish set. Let atomic number of an atom for current 0-bit is p and this atom is q-th in the start set. If we cover with this atom only part of the remainder of number of the (i+1)-th atom, dp2'[mask XOR (1<<q)]=(i,j+p). If we cover with this atom the remainder fully (and exactly this remainder, no more!), dp2'[mask XOR (1<<q)]=(i+1,0).
Now dp1 is useless. If at end dp2'[2n - 1]=(k,0), solution exists (it is easy to restore it), otherwise there is no solution.
B. At first, compute
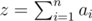 . It equals ⌊ mnk / 100⌋, where ⌊ x⌋ is rounding down. Next we fill first ⌊ z / k⌋ squares with a saturation k. (⌊ z / k⌋ + 1)-th square (if it exists) we fill in a saturation z - ⌊ z / k⌋ k. All other squares we leave with a saturation 0.
. It equals ⌊ mnk / 100⌋, where ⌊ x⌋ is rounding down. Next we fill first ⌊ z / k⌋ squares with a saturation k. (⌊ z / k⌋ + 1)-th square (if it exists) we fill in a saturation z - ⌊ z / k⌋ k. All other squares we leave with a saturation 0.C. Define an good polygon as a regular polygon which has a knight in a good mood in every of its vertex. Side of polygon we will measure in arcs which is obtained by dividing border of round table with knights.
Freeze the length of the side. Let this length equals k. Observe that the regular polygon with such length of side exists only if k divides n. We have exactly k of such polygons. Every of them has exactly n / k vertices. Check every of the polygons for goodness by review all of its vertices.
If sum of vertices with knight in a good mood equals to n / k, this polygon is good. Checking of all polygons with some frozen length of side works in an O(n).
Now observe that n has
 of divisors. Really, all divisors (may be except only one) we can divide into pairs (for i corresponds n / i, for i = n / i there is no pair). One of divisors in every pair less than
of divisors. Really, all divisors (may be except only one) we can divide into pairs (for i corresponds n / i, for i = n / i there is no pair). One of divisors in every pair less than  . It means thah number of pairs no more than
. It means thah number of pairs no more than  and number of divisors no more than
and number of divisors no more than 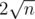 .
.It gives solution - iterate over all divisors of n and for every of them check existence of good polygon with length side equals this divisor. Solution has an
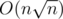 time.
time.In reality for big n is has
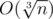 divisors. So solution actually has O(n4 / 3)-complexity. For all numbers less than 105 maximal number of divisors is 128.
divisors. So solution actually has O(n4 / 3)-complexity. For all numbers less than 105 maximal number of divisors is 128.UPD. There was found an
 solution by some participants. This solution uses following idea. If we have a good polygon with xy vertices, we also have a good polygon with x vertices. So we can check only prime divisors of n (except 2 - here we must check 4).
solution by some participants. This solution uses following idea. If we have a good polygon with xy vertices, we also have a good polygon with x vertices. So we can check only prime divisors of n (except 2 - here we must check 4).D. This problem can be divided into some subproblems.
Author's solution means following ones:
1. Check validness of square 3 × 3. Square is valid if all cards in it has equal suit or different rank. You may not check equal suit because equal suits imply different ranks.
2. Find 2 valid noninetsect squares 3 × 3 or return thah there are no ones. You can check all pairs of squares for inetsection. If some pair has no intersections check them with solution of subproblem 1.
3. Build set of cards which can be replaced with jokers. Generate full deck without jokers and drop from it all cards which in rectangle n × m are present.
4. Find number of jokers and its positions in rectangle.
5. Main subproblem. At first, solve subproblems 3 and 4. Now replace jokers in rectangle with cards from deck from subproblem 3 by all possible ways. For every replace solve subproblem 2. Arter all of variants of replacement just output answer.
There are O(n2m2) solution with small constant.
E. At first, you can use some search engine for find periodic table in some printable form. Next use copy-paste (one or several times) and format it by deleting all excess. It is mechanical work for no more than 5 minutes. Also some parser may be written. Note than author's solution does not mean write 100 symbols by hand from a picture. Next build some functions which transform symbols into numbers and vice versa.
So, we have some set of numbers. We need summarize some from them and get some another set of numbers. We will use dymanic programming over subsets.
Compute the first dp dp1[mask]->sum. For each subset calculate sum of numbers of all atoms in this subset. It can be done in O(2nn).
Now compute the second dp dp2[mask]->length. The "length" is a length of some prefix of result sequence of atoms which can be obtained by subset mask. If length -1, it means that it is impossible to get any prefix from this subset.
The second dp we can calculate in O(3n). Iterate over all masks and if dp2[mask]!=-1, iterate all its subsets of remained atoms (invert mask and get all its submasks). If some subset has sum of numbers which equals number of (dp2[маска]+1)-th atom from result set, recalculate dp2[mask XOR submask]=dp2[mask]+1.
At end, if dp2[2n - 1]=k, there are solution.
There are O(3n + 2nn) solution.
In this problem some brutforce solutions are passed because it is difficult to pick up some counterexample.
UPD. SkorKNURE found a solution in O(2nn). This solution is some modification of the author's solution.
Instead of dp2 calculate dp dp2'[mask]->(i,j), where i is a length of prefix which mask covers and j is part of number of (i+1)-th atom which mask covers.
Iterate over all masks. For each mask iterate over all its 0-bits (they are atoms which cover nothing from the finish set). We try to cover with this 0-bit a remainder of number of the (i+1)-th atom from the finish set. Let atomic number of an atom for current 0-bit is p and this atom is q-th in the start set. If we cover with this atom only part of the remainder of number of the (i+1)-th atom, dp2'[mask XOR (1<<q)]=(i,j+p). If we cover with this atom the remainder fully (and exactly this remainder, no more!), dp2'[mask XOR (1<<q)]=(i+1,0).
Now dp1 is useless. If at end dp2'[2n - 1]=(k,0), solution exists (it is easy to restore it), otherwise there is no solution.











(I feel proud of myself for this guess :))
For (C) it suffices to check polygons with a prime number of sides (except for 2, then check 4), that gives O(log n) divisors to check.
does dp1 calculation really need dynamic programming?
I think, this part can be done by simple 2 loops.
dp1[mask]=0;
for(int i=0;i<n;i++){
if(mask&(1<<i)) dp1[mask]+=(weight of i-th atom);
}
}
(Yes, I'm a necroposter)
Me too apparently
Why do I need to output $$$L - 2$$$?
see input vs output.. for less than 11 charactered string we print the string back but for string greater than 10 characters we print first char last char and length of string if those two chars weren't there