Операция  вводится на целых положительных числах.
вводится на целых положительных числах. 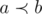 верно, если
верно, если 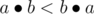 , где
, где 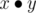 значит конкатенацию строковых представлений чисел x, y и последующий перевод результата в число.
значит конкатенацию строковых представлений чисел x, y и последующий перевод результата в число.
Требуется доказать, что если 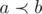 и
и 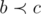 , то
, то 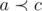 .
.
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 3993 |
| 2 | jiangly | 3743 |
| 3 | orzdevinwang | 3707 |
| 4 | Radewoosh | 3627 |
| 5 | jqdai0815 | 3620 |
| 6 | Benq | 3564 |
| 7 | Kevin114514 | 3443 |
| 8 | ksun48 | 3434 |
| 9 | Rewinding | 3397 |
| 10 | Um_nik | 3396 |
| Страны | Города | Организации | Всё → |
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 155 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 10 | nor | 152 |
Операция  вводится на целых положительных числах.
вводится на целых положительных числах. 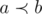 верно, если
верно, если 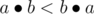 , где
, где 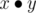 значит конкатенацию строковых представлений чисел x, y и последующий перевод результата в число.
значит конкатенацию строковых представлений чисел x, y и последующий перевод результата в число.
Требуется доказать, что если 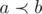 и
и 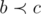 , то
, то 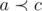 .
.
| Название |
|---|



Можно доказать, что , где a∞ — бесконечная циклическая строка, образованная строкой a. При таком определении транзитивность отношения будет очевидна.
, где a∞ — бесконечная циклическая строка, образованная строкой a. При таком определении транзитивность отношения будет очевидна.
Факт доказывается аккуратным рассмотрением, как работают оба варианта сравнения строк.
Можно доказать таким образом: Запишем три неравенства:
a*10^m+b<b*10^n+a(1)b*10^k+c<c*10^m+b(2)a*10^k+c<c*10^n+a(3), гдеn,m,kдлины чиселa,b,cсоответственно.Получаем:
a<b(10^n-1)/(10^m-1)(4) из (1)b<c(10^m-1)/(10^k-1)(5) из (2)b(10^n-1)/(10^m-1) < c(10^n-1)/(10^k-1)(6)a<c(10^n-1)/(10^k-1)из (4) и (6). Видим что получили неравенство (3)То же самое, но проще. L(x) — минимальная степень 10 большая чем x.
A * L(B) + B < B * L(A) + A (1)
A * (L(B) — 1) < B * (L(A) — 1) (2)
A / (L(A) — 1) < B / (L(B) — 1) (3). Транзитивность очевидна.
Если кому-то интересно, это компаратор для решения задачи "строку разрезали на k фрагментов. Вам даны фрагменты, какая лексикографически минимальная строка могла быть изначально?"