Производство остановится только в том случае, если существует такое целое K ≥ 0, что a·2K делится на m. Из этого следует, что K может быть максимум порядка log2(m). Так как K — это по сути сколько пройдёт дней до этого момента, то можно промоделировать описанные в условии задачи действия, например, в течение 20-ти дней (не забыв при этом про 64-битный тип данных). Если в какой-то момент производство остановилось, то ответ "Yes". Если не остановилось в течение этих дней, то оно не остановится никогда, а значит ответ "No".
Найдём минимальную длину, необходимую чтобы покрыть все точки по оси Ox — это будет в точности Maximum(xi) - Minumum(xi). Аналогично и для оси Oy — это Maximum(yi) - Minumum(yi). Так как нам необходим квадрат, то следует взять максимальную из этих двух величин в качестве длины его стороны.
Опишем функцию f(L, R), которая будет ответом на задачу. Она ведёт себя следующим образом:
если L = R, то f(L, R) = L;
иначе, если 2b ≤ L, где b — максимальное целое число такое, что 2b ≤ R, то f(L, R) = f(L - 2b, R - 2b) + 2b;
иначе, если 2b + 1 - 1 ≤ R, то f(L, R) = 2b + 1 - 1;
иначе f(L, R) = 2b - 1.
Итоговая сложность — O(logR) на один запрос.
Переберём все различные числа aj исходной последовательности. Так как нужно максимизировать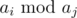 
, то переберём в цикле по x все числа, кратные aj в диапазоне от 2aj до M, где M — удвоенное максимальное значение элемента последовательности. Для каждого такого числа нужно найти максимальное ai, такое, что ai < x. Ограничения на числа позволяют сделать это за O(1) при помощи массива. Обновим ответ величиной 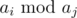. Так как перебираются только различные aj, то итоговая сложность составит O(nlogn + MlogM).
Заметим, что d-сортировка не зависит от того, какие символы находятся в строке, а значит является перестановкой (назовём её P). Посмотрим на операцию перемешивания по другому: вместо того, чтобы переходить к очередной следующей подстроке и сортировать её, сделаем циклический сдвиг всей строки на один символ влево. Таким образом, сортироваться будет только префикс строки, а строка сдвигаться. Осталось понять, что сдвиг влево — это тоже перестановка (назовём её C). Теперь всё просто, к строке нужно поочерёдно применять перестановки P и C, то есть нужно получить S·P·C·P·C... = S·(P·C)n - k + 1. После этого строку нужно сдвинуть ещё на k - 1 символ влево, чтобы получить то, что получится после операции перемешивания. Здесь используется умножение перестановок, а оно в свою очередь ассоциативно, а значит для вычисления (P·C)n - k + 1 можно воспользоваться бинарным алгоритмом. Итоговая сложность составит O(nmlogn).
Заметим, что существует оптимальный ответ такой, что любой отрезок, который образует группу, содержит свои максимальные и минимальные значения на границах. Иначе было бы выгодно разбить отрезок хотябы на два. Так же можно заметить, что каждый отрезок будет строго монотонным (элементы на нём строго возрастают или убывают). Выделим интересные точки в последовательности — это либо локальные максимумы (то есть ai - 1 < ai > ai + 1), либо минимумы (ai - 1 > ai < ai + 1), либо соседние с ними точки. Будем решать задачу методом динамического программирования, Di — наилучший ответ для префикса i. Тогда при вычислении очередного значения необходимо обработать не более трёх предыдущих интересных точек, а так же предыдущую точку. Итоговая сложность — O(n).
Заметим, что при поиске ответа на конкретный запрос можно воспользоваться бинарным поиском по ответу. Пусть в какой-то момент зафиксировалась высота h и необходимо узнать, помещается ли прямоугольник размера w на h в участок забора с l-ой по r-ой доски включительно. Заведём перед обработкой запросов структуру данных, которая поможет отвечать на такой вопрос. Это будет персистентное дерево отрезков с необычной функцией: максимальное количество подряд идущих единиц на отрезке (далее maxOnes). В листьях дерева будут только числа 0 и 1. Чтобы реализовать такую функцию, необходимо ввести ещё некоторые величины, а именно:
len — длина отрезка в вершине дерева отрезков, prefOnes — длина префикса, полностью состоящего из единиц, sufOnes — длина суффикса, полностью состоящего из единиц.
Вычисляются эти функции следующим образом:
maxOnes, требуемая функция, равна max(maxOnes(Left), maxOnes(Right), sufOnes(Left) + prefOnes(Right));
prefOnes равна prefOnes(Right) + len(Left) в случае, если len(Left) = prefOnes(Left), иначе она равна prefOnes(Left);
sufOnes равна sufOnes(Left) + len(Right) в случае, если len(Right) = sufOnes(Right), иначе она равна sufOnes(Right);
len = len(left) + len(Right);
Left и Right — соответственно левый и правые сыновья текущей вершины в структуре дерева отрезков.
Как уже упоминалось выше, дерево должно быть персистентным (то есть хранить все свои версии после изменений), строиться оно должно следующим образом. Сначала строится пустое дерево — из одних нулей. Далее в позицию, где в заборе находится самая высокая доска, ставится единица. Тоже самое делается для второй по убыванию высоты доски и так далее. Например, если забор описывался последовательностью [2, 5, 5, 1, 3], то изменения последнего слоя дерева будут следующими:
[0, 0, 0, 0, 0] -> [0, 1, 0, 0, 0] -> [0, 1, 1, 0, 0] -> [0, 1, 1, 0, 1] -> [1, 1, 1, 0, 1] -> [1, 1, 1, 1, 1].
При этом для каждой высоты hi нужно запомнить соответствующую версию дерева, назовём её как treeheight. Теперь, чтобы ответить на вопрос выше, нужно сделать запрос на отрезке [l, r] у дерева treeh. Если maxOnes этого запроса меньше w, то прямоугольник невозможно разместить, иначе возможно.
Построение дерева займёт O(nlogn) времени и памяти. Ответ на запрос займёт O(log2n) времени.
After reading the editorials problems seem to be very easy
I think problems are also easy before reading the tutorial. Idiot !
If they are easy, why do you solve just one problem?
Too skilled to solve beginner problems maybe...
Нам нужна не коммутативность произведения перестановок, а ассоциативность.
"Since they are commutative (permutations)" — they are not. I think you meant "associative".
умножение перестановок не комматутивно, но оно и не нужно. нужна ассоциативность.
Problem E can be solved by divide and conquer.
I tried to think about this approach during the contest but didn't come up with a solid solution. Could you share your idea?
Maybe "parallel binary search" is a better term to describe this.
Could you please decsribe it in more detail?
I think in this code it is pretty nice implemented and you can learn it from here 8573776. You don't need to read the whole solution, just read what is going in a while loop in main and in bsearch function.
Here is another problem where you can find that technique useful http://main.edu.pl/en/archive/oi/18/met
Yes, "parallel binary search" is a better term ~~
Wonderful solution. A new tech was got.
Could someone tell me why do we know K maximum is O(logm) in A?
ok
I was trying D like this , First sort the array. Then iterate through the array , and
Here my observation was that , for each number , the maximum would be in just the number after divide by 2,3,4 ... . But I wasn't sure how upto which number I have to divide. Can someone tell ? Its look like I did the reverse thing of the editorial .
Like you said, the naive approach is to loop over each a_i, and for each j in 2...a_i, find the upper bound of a_i / j in a and update the maximum.
For a_i = 1e6, there are roughly 2K distinct values of a_i / j. We'd like to search each of these integers once. Once we increment j to the point where a_i / j and a_i / (j+1) just differ by one, we can just search all integers from a_i / (j+1) down to the current maximum.
Finally, we can find the upper bound in constant time by memorizing it. You can see my implementation at http://codeforces.me/contest/484/submission/8579751.
can you explain a bit , how did you find upper bound in constant time ? will it work if I use the library lgn upper_bound ? and thanks , counting upto M was the main trick I was missing. I thought I had to count upto first element every time
484B - Maximum Value Can anyone explain me why we iterate x in range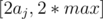
? I think every x in range 
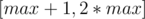then the ai we need to find is certainly max => We only need to consider range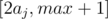 
Yes I also think there's no need for that.But max+1 is wrong as we are only checking for integer multiples of aj so we will leave out max as there is no number greater than it in the range.
Instead
Let p=(max/aj)
integer division. A range of [ 2*aj, (p+1)*aj ] is sufficient.Accepted solution 8590333
Can you tell me what is if(i&&arr[i]==arr[i-1]) continue; means?
There can be more than one occurrences of a number and there's no point in calculating again as answer for both of them will be same, that's why we need to consider only distinct numbers. For that condition
arr[i]!=arr[i-1]will work as array is sorted.Now what if
i=0above condition will checkarr[0]!=arr[-1].So to avoid this conditioniis used.If
i is 0i&&arr[i]!=arr[i-1]will become0&&arr[i]!=arr[i-1]. Since first is falsearr[i]!=arr[i-1]doesn't gets executed.Together it makes
if(i&&arr[i]!=arr[i-1])In the explanation of Problem A-Factory, Author said,
Production will stops iff exists integer K ≥ 0 such a*POW(2,K) is divisible by m.I can't understand this part. Can anyone please explain or prove why this statement is true. Thanks(a + (a mod m)) mod m = ((a mod m) + (a mod m)) mod m = (2*a) mod m
Lets define (a mod m) as p. We just need to prove that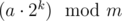
is the reminder after k-th step. We can prove that by induction. The case k = 0 is trivial. Here is the inductive step:
We prove that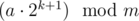
is the doubled residue from the k-th step.
Just FYI: in B it was also possible to squeeze O(nlognlogM), even on JVM: 8579216 (by using binary search instead of a precomputed array).
Well, I wouldn't say squeeze actually. My solution (8566302) works in 389 ms.
how is time complexity of 484B -Maximum Value calculated
MlogM? It is harmonic series, M / 1 + M / 2 + M / 3 + ....
harmonic is O(logn)
Тогда при вычислении очередного значения необходимо обработать не более трёх предыдущих интересных точек, а так же предыдущую точку.Достаточно двух точек: если убываем, то точку начала убывания и предыдущую, если возрастаем, то точку начала возрастания и предыдущую.Выведете максимальную возможную суммарную общительность всех групп.Давайте писать грамотно: вывед**и**те.И выделение жирным отдельного символа не работает.
Не могли ли вы объяснить почему надо рассматривать предыдущие точки, ведь они могут испортить нашу монотонность?
There is also O(n + M) solution for B (Maximum Value); like this one : 8569709
Awesome!... This is beautiful!
It seems that this solution doesn't work on this test.
The correct answer is 5 (53 mod 6), but this solution prints 4 (53 mod 7).
Successful hacking attempt!! :D
Думаю, в третьей задаче первого дивизиона в формуле ai - 1 < ai > ai + 1 знаки неравенства должны быть нестрогими, т.к. возможно нам будет выгодно сделать разрез между одинаковыми элементами. По крайней мере я это учитывал.
Could someone explain idea of these(8598536,8580448) solutions of problem E? They are the fastest, offline and haven't persistent tree or parallel binary search.
for each ai, we can get l[i] and r[i],which means the maximum interval that contains ai and ai is the minimum number,and we get n intervals, sort them by length, also sort queries by length. When handling with a query(l,r,w), use segment tree to maintain those intervals whose length is not smaller than w.
В разборе задачи D (Div2):
Для каждого такого числа нужно найти максимальное ai, такое, что ai < x. Ограничения на числа позволяют сделать это за O(1) при помощи массива.Подскажите, пожалуйста, как это можно сделать. Я использую бинарный поиск для этого, однако такое решение получает TLE.484B - Maximum Value — How to find maximum in O(1) ?
Sort the array and just maintain another array
Aof10^6elements whereindex i stores element just smaller than iFor example consider sorted array
[2,4,7,11], thenA(0 indexed) will be[-1,-1,-1,2,2,4,4,4,7,7,7,7,11...]-1 means no element is smaller than i.So?After that?Can you please post your solution?
It was not clear to me .(
Let $$$x$$$ be 5, for instance you want to find max element which is smaller than 5 in our array(no matter if 5 exists in array or not). It is simply A[5], as mentioned above each index $$$i$$$ in A contains smaller element than $$$i$$$. So in array above A[5] = 4.
I solved problem "484A — Bits" in an easy way. While L is less than or equals to R, I set the unsetted bits of L from left to right. The solution got ACCEPTED :)
My Solution
have an explanation?
Yes, for sure. I wanna maximize the popcount to a value between L and R. I have an initial value L, how can I increase the popcount by one without decrease the number, minimizing the value of the resulting number? The answer is: Set the less significative bit that is zero. If you repeat this operation while the number is less than R you will find the answer.
For example: I have the number:
100101
To increase the popcount without decrease the number, the best thing to do is to set the second bit:
100111
There is no other configuration that is bigger than 100101 and less than 100111 with popcount equals to 4.
It's a very good solution, a lot better than the editorial!
Awesome!
485-B Test# 7 gives correct answer on my compiler but wrong on the online one. Used long int (C++11) but still not working. Any suggestions?
Use
long longIn problem A, I used different approach..not sure how bad my complexity is..but here's the idea.
Given a & m
Suppose a=km +x
Now, a%m =x For the next iteration a = a prev + x = (km + x) + x = km + 2x
So,remainders will be {x,2x,3x...}
Now,after some point of time,If I again get remainder x,then it means
a= lm +x So,clearly for next iteration I will be getting remainder 2x and so on
So remainders will again repeat as {x,2x,3x...}
Hence if an already occurred, remainder occurs again..production never scores.... and if in some point of time I get remainder 0,then clearly production stops.
I used a STL map to store remainders.
I didn't participated in the contest, solved it during practice. My code link is http://codeforces.me/contest/485/submission/11278079 Thanks
I solved DIV1-D using a different approach; define dp[i][j] (0 <= i <= 1) as the best answer of the subarray from [0, j]. dp[i][j] will hold 3 things:
1) the answer
2) min element of the last segment
3) max element of the last segment
dp[1][j] means that a[j] is the starting the last segment, dp[0][j] means a[j] is appended to the last segment. The recurrence relation is as follows:
— dp[1][j] = dp[0][j — 1] (update min & max to a[j])
— dp[0][j] = best_of (appending a[j] to dp[0][j — 1], appending a[j] to dp[1][j — 1])
[submission:http://codeforces.me/contest/484/submission/31842418]
In the problem Maximum Value, why do we search for the maximum a_i such that a_i < x ?
I came across problem Div 2 C back when I was a beginner and I could not solve it or understand the editorial. Today I solved this question and wrote an editorial of my own here.
Feel free to read it. I explain it in a lot of detail :)
484A-Bits: let curr=log2(1e18) starting from i=curr. find the leftmost bit(say i-th bit) of L which we can set, still keeping L<=R. now, for all bits to the right of this i-th bit, set them. also set i-th bit if it still remains L<=R. final L is the answer!
I solved Div1A Bits a bit differently. Its a kind of a greedy approach that uses recursion, checking the bits of a l and r from left to right. If anyone is interested I'll give an explanation.
https://codeforces.me/contest/484/submission/48948769
Div2 C/ Div1 A __builtin_popcount() gave me wrong answer on test 11. Code
After i've calculated number of set bits manually, Got AC. Code
I even dont know why.Can anyone explain?
__builtin_popcount for int32
__builtin_popcountll for int64
Production will stops iff exists integer K ≥ 0 such a·2K is divisible by m. From this fact follows that K maximum will be about O(log2(m)).
For 485A- Factory, can someone explain these lines from the editorial?
My solution for 484ABits is different. if a=l^r; the MSB in a would be the biggest bit in r that is set but unset in l. So in l,just turn on all the bits after the MSB in a:that is the answer. Also account for the fact that r itself could be an answer and check: if all the bits FROM msb in a is set in r, then r is the answer,else we get answer by above method_