Production will stops iff exists integer K ≥ 0 such a·2K is divisible by m. From this fact follows that K maximum will be about O(log2(m)). So if we modeling some, for example, 20 days and production does not stop, then it will never stop and answer is "No". Otherwise answer is "Yes".
Let us find minimum length needed to cover points by Ox. It is Maximum(xi) - Minumum(xi). The same in Oy — Maximum(yi) - Minumum(yi). Since we need a square city to cover all the mines, then we need to set length of this square to the maximum from those two values.
Let us define function f(L, R), that gives answer to the query. It looks follows:
if L = R then f(L, R) = L;
else if 2b ≤ L, where b — maximum integer such 2b ≤ R, then f(L, R) = f(L - 2b, R - 2b) + 2b;
else if 2b + 1 - 1 ≤ R then f(L, R) = 2b + 1 - 1;
else f(L, R) = 2b - 1.
Total complexity is O(logR) per query.
Let us iterate over all different aj. Since we need to maximize 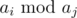 , then iterate all integer x (such x divisible by aj) in range from 2aj to M, where M — doubled maximum value of the sequence. For each such x we need to find maximum ai, such ai < x. Limits for numbers allow to do this in time O(1) with an array. After that, update answer by value
, then iterate all integer x (such x divisible by aj) in range from 2aj to M, where M — doubled maximum value of the sequence. For each such x we need to find maximum ai, such ai < x. Limits for numbers allow to do this in time O(1) with an array. After that, update answer by value 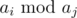 . Total time complexity is O(nlogn + MlogM).
. Total time complexity is O(nlogn + MlogM).
Note, that d-sorting is just a permutation (call it P), because it does not depends on characters in string. Look at shuffling operation in different way: instead of going to the next substring and sort it, we will shift string to one character left. It remains to understand that shift of string the permutation too (call it C). Now its clear, we need to calculate S·P·C·P·C... = S·(P·C)n - k + 1. And after that shift string for k - 1 character to the left for making answer to the shuffling operation. Here we use the multiplication of permutations. Since they are associative, that we can use binary algorithm to calculate (P·C)n - k + 1. Total time complexity is O(nmlogn).
Let us note, that in optimal answer any segment that making a group contains their minimum and maximum values on borders. Otherwise it will be better to split this segment to two other segments. Another note that is every segment in optimal solution is strictly monotonic (increasing or decreasing). Paying attention to the interesting points in sequence which making local maximums (i. e. ai - 1 < ai > ai + 1), local minimums (ai - 1 > ai < ai + 1), and point adjacent to them. Solve the problem by dynamic programming: Di is the answer in the prefix i. To calculate Di we need to look at no more than three previous interesting points and to previous Di - 1. Total time complexity is O(n).
Let us note that we can use binary search to find answer to the one query. Suppose at some moment was fixed height h and need to know will fit the rectangle with width w and height h to the segment of fence from l-th to r-th panel. Let us build data structure that can answer to this question. This will be persistent segment tree with unusual function inside: maximum number of consecutive ones in segment (maxOnes). In leaves of segment tree will be only numbers 0 and 1. To calculate this function need to know some other values, specifically:
len — length of the segment in vertex of segment tree, prefOnes — length of prefix that consists only of ones, sufOnes — length of the suffix consist only of ones.
These functions are computed as follows:
maxOnes is equal to max(maxOnes(Left), maxOnes(Right), sufOnes(Left) + prefOnes(Right));
prefOnes equals prefOnes(Right) + len(Left) in case of len(Left) = prefOnes(Left), and prefOnes(Left) otherwise;
sufOnes equals sufOnes(Left) + len(Right) in case of len(Right) = sufOnes(Right), and sufOnes(Right) otherwise;
len = len(left) + len(Right);
Left и Right — it is left and right sons of vertex in segment tree.
As mentioned above, tree must be persistent, and it must be built as follows. First, builded empty tree of zeros. Next in position of highest plank need to put 1. The same doing for planks in decreasing order. For example if fence described with sequence [2, 5, 5, 1, 3] then bottom of segment tree will changed as follows:
[0, 0, 0, 0, 0] -> [0, 1, 0, 0, 0] -> [0, 1, 1, 0, 0] -> [0, 1, 1, 0, 1] -> [1, 1, 1, 0, 1] -> [1, 1, 1, 1, 1].
And we need to remember for all hi their version of tree. Now to answer the question we need to make query in our segment tree (that corresponding to height h) on segment [l, r]. If maxOnes form this query less than w, then rectangle impossible to put (otherwise possible).
Building of tree will take O(nlogn) time and memory. Time complexity to the one query will take O(log2n) time.











After reading the editorials problems seem to be very easy
I think problems are also easy before reading the tutorial. Idiot !
If they are easy, why do you solve just one problem?
Too skilled to solve beginner problems maybe...
"Since they are commutative (permutations)" — they are not. I think you meant "associative".
Problem E can be solved by divide and conquer.
I tried to think about this approach during the contest but didn't come up with a solid solution. Could you share your idea?
Maybe "parallel binary search" is a better term to describe this.
Could you please decsribe it in more detail?
I think in this code it is pretty nice implemented and you can learn it from here 8573776. You don't need to read the whole solution, just read what is going in a while loop in main and in bsearch function.
Here is another problem where you can find that technique useful http://main.edu.pl/en/archive/oi/18/met
Yes, "parallel binary search" is a better term ~~
Wonderful solution. A new tech was got.
Could someone tell me why do we know K maximum is O(logm) in A?
ok
I was trying D like this , First sort the array. Then iterate through the array , and
Here my observation was that , for each number , the maximum would be in just the number after divide by 2,3,4 ... . But I wasn't sure how upto which number I have to divide. Can someone tell ? Its look like I did the reverse thing of the editorial .
Like you said, the naive approach is to loop over each a_i, and for each j in 2...a_i, find the upper bound of a_i / j in a and update the maximum.
For a_i = 1e6, there are roughly 2K distinct values of a_i / j. We'd like to search each of these integers once. Once we increment j to the point where a_i / j and a_i / (j+1) just differ by one, we can just search all integers from a_i / (j+1) down to the current maximum.
Finally, we can find the upper bound in constant time by memorizing it. You can see my implementation at http://codeforces.me/contest/484/submission/8579751.
can you explain a bit , how did you find upper bound in constant time ? will it work if I use the library lgn upper_bound ? and thanks , counting upto M was the main trick I was missing. I thought I had to count upto first element every time
484B - Maximum Value Can anyone explain me why we iterate x in range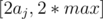 ? I think every x in range
? I think every x in range 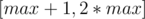 then the ai we need to find is certainly max => We only need to consider range
then the ai we need to find is certainly max => We only need to consider range 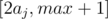
Yes I also think there's no need for that.But max+1 is wrong as we are only checking for integer multiples of aj so we will leave out max as there is no number greater than it in the range.
Instead
Let p=(max/aj)
integer division. A range of [ 2*aj, (p+1)*aj ] is sufficient.Accepted solution 8590333
Can you tell me what is if(i&&arr[i]==arr[i-1]) continue; means?
There can be more than one occurrences of a number and there's no point in calculating again as answer for both of them will be same, that's why we need to consider only distinct numbers. For that condition
arr[i]!=arr[i-1]will work as array is sorted.Now what if
i=0above condition will checkarr[0]!=arr[-1].So to avoid this conditioniis used.If
i is 0i&&arr[i]!=arr[i-1]will become0&&arr[i]!=arr[i-1]. Since first is falsearr[i]!=arr[i-1]doesn't gets executed.Together it makes
if(i&&arr[i]!=arr[i-1])In the explanation of Problem A-Factory, Author said,
Production will stops iff exists integer K ≥ 0 such a*POW(2,K) is divisible by m.I can't understand this part. Can anyone please explain or prove why this statement is true. Thanks(a + (a mod m)) mod m = ((a mod m) + (a mod m)) mod m = (2*a) mod m
Lets define (a mod m) as p. We just need to prove that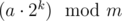 is the reminder after k-th step. We can prove that by induction. The case k = 0 is trivial. Here is the inductive step:
is the reminder after k-th step. We can prove that by induction. The case k = 0 is trivial. Here is the inductive step:
We prove that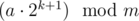 is the doubled residue from the k-th step.
is the doubled residue from the k-th step.
Just FYI: in B it was also possible to squeeze O(nlognlogM), even on JVM: 8579216 (by using binary search instead of a precomputed array).
Well, I wouldn't say squeeze actually. My solution (8566302) works in 389 ms.
how is time complexity of 484B -Maximum Value calculated
MlogM? It is harmonic series, M / 1 + M / 2 + M / 3 + ....
harmonic is O(logn)
There is also O(n + M) solution for B (Maximum Value); like this one : 8569709
Awesome!... This is beautiful!
It seems that this solution doesn't work on this test.
The correct answer is 5 (53 mod 6), but this solution prints 4 (53 mod 7).
Successful hacking attempt!! :D
Could someone explain idea of these(8598536,8580448) solutions of problem E? They are the fastest, offline and haven't persistent tree or parallel binary search.
for each ai, we can get l[i] and r[i],which means the maximum interval that contains ai and ai is the minimum number,and we get n intervals, sort them by length, also sort queries by length. When handling with a query(l,r,w), use segment tree to maintain those intervals whose length is not smaller than w.
484B - Maximum Value — How to find maximum in O(1) ?
Sort the array and just maintain another array
Aof10^6elements whereindex i stores element just smaller than iFor example consider sorted array
[2,4,7,11], thenA(0 indexed) will be[-1,-1,-1,2,2,4,4,4,7,7,7,7,11...]-1 means no element is smaller than i.So?After that?Can you please post your solution?
It was not clear to me .(
Let $$$x$$$ be 5, for instance you want to find max element which is smaller than 5 in our array(no matter if 5 exists in array or not). It is simply A[5], as mentioned above each index $$$i$$$ in A contains smaller element than $$$i$$$. So in array above A[5] = 4.
I solved problem "484A — Bits" in an easy way. While L is less than or equals to R, I set the unsetted bits of L from left to right. The solution got ACCEPTED :)
My Solution
have an explanation?
Yes, for sure. I wanna maximize the popcount to a value between L and R. I have an initial value L, how can I increase the popcount by one without decrease the number, minimizing the value of the resulting number? The answer is: Set the less significative bit that is zero. If you repeat this operation while the number is less than R you will find the answer.
For example: I have the number:
100101
To increase the popcount without decrease the number, the best thing to do is to set the second bit:
100111
There is no other configuration that is bigger than 100101 and less than 100111 with popcount equals to 4.
It's a very good solution, a lot better than the editorial!
Awesome!
485-B Test# 7 gives correct answer on my compiler but wrong on the online one. Used long int (C++11) but still not working. Any suggestions?
Use
long longIn problem A, I used different approach..not sure how bad my complexity is..but here's the idea.
Given a & m
Suppose a=km +x
Now, a%m =x For the next iteration a = a prev + x = (km + x) + x = km + 2x
So,remainders will be {x,2x,3x...}
Now,after some point of time,If I again get remainder x,then it means
a= lm +x So,clearly for next iteration I will be getting remainder 2x and so on
So remainders will again repeat as {x,2x,3x...}
Hence if an already occurred, remainder occurs again..production never scores.... and if in some point of time I get remainder 0,then clearly production stops.
I used a STL map to store remainders.
I didn't participated in the contest, solved it during practice. My code link is http://codeforces.me/contest/485/submission/11278079 Thanks
I solved DIV1-D using a different approach; define dp[i][j] (0 <= i <= 1) as the best answer of the subarray from [0, j]. dp[i][j] will hold 3 things:
1) the answer
2) min element of the last segment
3) max element of the last segment
dp[1][j] means that a[j] is the starting the last segment, dp[0][j] means a[j] is appended to the last segment. The recurrence relation is as follows:
— dp[1][j] = dp[0][j — 1] (update min & max to a[j])
— dp[0][j] = best_of (appending a[j] to dp[0][j — 1], appending a[j] to dp[1][j — 1])
[submission:http://codeforces.me/contest/484/submission/31842418]
In the problem Maximum Value, why do we search for the maximum a_i such that a_i < x ?
I came across problem Div 2 C back when I was a beginner and I could not solve it or understand the editorial. Today I solved this question and wrote an editorial of my own here.
Feel free to read it. I explain it in a lot of detail :)
484A-Bits: let curr=log2(1e18) starting from i=curr. find the leftmost bit(say i-th bit) of L which we can set, still keeping L<=R. now, for all bits to the right of this i-th bit, set them. also set i-th bit if it still remains L<=R. final L is the answer!
I solved Div1A Bits a bit differently. Its a kind of a greedy approach that uses recursion, checking the bits of a l and r from left to right. If anyone is interested I'll give an explanation.
https://codeforces.me/contest/484/submission/48948769
Production will stops iff exists integer K ≥ 0 such a·2K is divisible by m. From this fact follows that K maximum will be about O(log2(m)).
For 485A- Factory, can someone explain these lines from the editorial?
My solution for 484ABits is different. if a=l^r; the MSB in a would be the biggest bit in r that is set but unset in l. So in l,just turn on all the bits after the MSB in a:that is the answer. Also account for the fact that r itself could be an answer and check: if all the bits FROM msb in a is set in r, then r is the answer,else we get answer by above method_