Рассмотрим сначала случай, когда все числа отличны от нуля. Тогда можно взять a*c*e граммов песка, получить из них b*c*e граммов свинца, из них - b*d*e граммов золота, из них - b*d*f граммов песка. Если b*d*f > a*c*e, то можно неограниченно увеличивать количество песка, а, соответственно, и золота. В противном случае, когда b*d*f <= a*c*e, сколь угодно большое количество золота получить невозможно. То же самое верно, если у дроби (a*c*e)/(b*d*f) только числитель или только знаменатель равен нулю. В противном случае возникает неопределенность 0/0 и нужно делать отдельную проверку случаев.

Поясню, почему я сделала эту задачу именно задачей A. 

1. Для решения задачи требуются совсем незначительные знания по программированию (только if), поэтому она была доступна всем участникам.

2. Хитрые случаи действительно были, но я понадеялась, что "сильные участники ... помогут новичкам отловить все баги своими взломами". Так оно и вышло.

Хотя, возможно, я была не права: эта задача слишком сложная для А. 

Большое количество взломов по этой задаче - вполне предвиденное обстоятельство. Специально оставила большой класс тестов, не вошедший в претесты, чтобы было интереснее ломать. Ради справедливости стоит отметить, что Артем Рахов был против этого. В связи с этой задачей остро всплыла проблема, о которой написал Gassa: претесты отражают весьма неполный набор случаев и заранее непонятно, какой это набор и как интерпретировать событие "решение прошло претесты". Мне кажется, стоит обсудить этот вопрос и четко определить принципы разработки претестов.

Задача решается жадно. Заменим одну цифру в первой дате таким образом, чтобы год получился наименьшим возможным. На каждом следующем шаге будем перебирать все замены одной цифры в очередной дате и выбирать такую, которая делает дату не меньше предыдущей и при этом как можно меньшей. Если последний год не превзошел 2011 - решение найдено. Иначе решения не существует.

Как это доказать? Рассмотрим некоторое правильное решение. Ясно, что если первая дата в нем не совпадает с наименьшим числом, которое можно получить из первого заданного, то можно заменить ее на это число. Вторую дату также можно заменить на наименьшее возможное число, не превосходящее первого и т.д. В результате мы получим из любого решения тот жадный вариант, который научились строить. А если такого жадного варианта не существует - то и решения не существует.

Будем отдельно для каждого звена ломаной определять, может ли Гарри поймать снитч на нем. Заметим, что так как v_p ≥ v_s, то если Гарри может поймать снитч в некоторый момент времени, то он сможет поймать его и в более поздний момент времени. Он сможет просто лететь за снитчем по его траектории. Поэтому используем бинарный поиск на каждом отрезке.

Отдельно остановлюсь на проблемах с EPS, возникших у участников. Проблемы могли возникнуть из-за того, что

1) некоторый EPS стоял в условии: while (leftTime + EPS < rightTime) <делать бинпоиск>. В задаче нужно было с определенной точностью выводить не только время, но и координаты точки. Если время отличается от правильного не больше, чем на EPS, то координаты точки могут отличаться значительно сильнее. В таких случаях нужно сравнивать не аргумент функции, а саму функцию с EPS. Или, как обычно делаю я и что однажды не понравилось преподавателю по численным методам, делать некоторое фиксированное количество итераций бинпоиска (например, 60).

2) EPS в сравнении времен внутри бинпоиска вроде этого:

if (currentTime + addTime > distance / potterSpeed - EPS)

                                                rightTime = currentTime;

                                        else

                                                leftTime = currentTime;

Здесь его вообще лучше убрать. Или поставить EPS значительно меньше по сравнению с точностью, с которой надо выводить точку.

(Приведенные фрагменты кода - из решения Егора.)

Обозначим через S_i множество всевозможных распределений первых i по учеников по факультетам, представляющее собой множество четверок вида (a₁, a₂, a₃, a₄), где a₁ - количество учеников, отправленных в Гриффиндор, a₂ - в Когтевран и т.д. Интуитивно понятно, что эти множества будут небольшими. Поэтому можно, тривиальным образом переходя от S_i - 1 к S_i, получить S_n, и по нему определить ответ.

Как же все-таки строго обосновать такой алгоритм? Пусть имеется некоторое множество S = {(aⁱ₁, aⁱ₂, aⁱ₃, aⁱ₄)}_{i = 1, 2, ..., k}. Представим его элементы в виде aⁱ_j = b_j + xⁱ_j, xⁱ_j ≥ 0, причем b_j выбраны максимально возможными, т.е. для любого j найдется i, такое, что xⁱ_j = 0. Назовем кортеж (b₁, b₂, b₃, b₄) базовой частью для S, а множество {(xⁱ₁, xⁱ₂, xⁱ₃, xⁱ₄)}_{i = 1, 2, ..., k} -- вариантной частью. 

В самом начале для S₀ и базовая, и вариантная части равны нулю. Проследим, как изменяются базовая и вариантная часть при рассмотрении очередного ученика. Если для этого ученика факультет фиксирован, но изменится только базовая часть. Она увеличится на 1 в позиции, соответствующей факультету. Из этого, в частности, следует, что можно получить множество с любой базовой частью (поскольку заданная во входном файле строка может содержать любую комбинацию символов G, H, R, S). Если же очередной символ в строке '?', то это может повлиять на изменение и базовой, и вариантной частей.

Например, для строки '????' имеем:

S₀ = {(0 + 0, 0 + 0, 0 + 0, 0 + 0)},

S₁ = {(0 + 1, 0 + 0, 0 + 0, 0 + 0), (0 + 0, 0 + 1, 0 + 0, 0 + 0), (0 + 0, 0 + 0, 0 + 1, 0 + 0), (0 + 0, 0 + 0, 0 + 0, 0 + 1)},

S₂ = {(0 + 1, 0 + 1, 0 + 0, 0 + 0), (0 + 1, 0 + 0, 0 + 1, 0 + 0), (0 + 1, 0 + 0, 0 + 0, 0 + 1), (0 + 0, 0 + 1, 0 + 1, 0 + 0), (0 + 0, 0 + 1, 0 + 0, 0 + 1), (0 + 1, 0 + 0, 0 + 1, 0 + 1)},

S₃ = {(0 + 1, 0 + 1, 0 + 1, 0 + 0), (0 + 1, 0 + 1, 0 + 0, 0 + 1), (0 + 1, 0 + 0, 0 + 1, 0 + 1), (0 + 0, 0 + 1, 0 + 1, 0 + 1)\},

S₄ = {(1 + 0, 1 + 0, 1 + 0, 1 + 0)}.

Исследуем вопрос о том, какой вид может иметь вариантная часть. Ее можно рассматривать независимо от базовой, учитывая при этом, что базовая может быть любой. Рассмотрим орграф, вершинами которого являются вариантные части, а ребра определяются тем, существует ли хотя бы одна базовая часть, при которой от одной вариантной части можно перейти к другой. Нас интересуют лишь те вершины, которые достижимы из {(0, 0, 0, 0)}.

Утверждение. Для всех достижимых из нуля вершин

(1) xⁱ_j ≤ 2,

(2) k ≤ 13.

Докажем, что все не обладающие свойствами (1) и (2) вершины недостижимы из нуля. Пусть имеется вариантная часть, обладающая свойством (1). Чтобы перебрать переходы из нее, нужно рассмотреть все возможные базовые части. Заметим, что достаточно рассмотреть базовые части, состоящие из чисел 0, 1, 2, 3 и содержащие хотя бы один 0. Действительно, базовая часть влияет на то, какие элементы будут минимальными, и к ним буде прибавление единицы. Базовую часть всегда можно нормировать, чтобы она содержала хотя бы один 0. Если базовая часть содержит числа больше 3, то соответствующие позиции никогда не будут минимальными (т.к. 4+0 > 0+2) и их можно эквивалентным образом заменить на 3 (3+0 > 0+2).

К сожалению, мои попытки рассмотрения случаев вручную ни к чему не привели, поэтому я написала программу, которая обходит описанный граф. Начиная из вершины 0, она строит переходы, перебирая лишь "маленькие" базовые части, описанные в предыдущем абзаце. В итоге эта программа перебирает все достижимые вариантные части (их оказывается чуть больше 1000) и проверяет, что они удовлетворяют условиям (1) и (2). Кроме того, программа позволяет построить тест с k = 13.

Рассмотрим граф, вершинами которого являются этажи, а ребрами - лестницы. Ясно, что, не двигая лестниц, Гарри сможет посетить всю компоненту связности, в которой находится его текущее местоположение. 

Каждое ребро может быть использовано для достижения новой вершины не более, чем два раза. Если компонента связности содержит n вершин и m ребер, то при обходе этой компоненты мы используем только n - 1 ребро для достижения новой вершины. Остальные m - n + 1 ребро не будут использованы для достижения новой вершины при их изначальном расположении. Поэтому они будут использованы для достижения новой вершины не более чем по одному разу. 

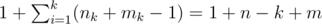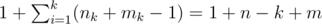Получаем, что используя ребра только одной компоненты связности, можно достичь не более чем n + m - 1 новых вершин. Всего получается не более чем достижимых вершин. Если m < k - 1, то получается, что все вершины посетить невозможно.

Покажем, что в противном случае (m >= k - 1) и если степень вершины 1 отлична от нуля, можно обойти все вершины. Иначе говоря, можно будет придумать такой порядок обхода, чтобы можно было переместить каждое из ребер. Будем обходить текущую компоненту обходом в глубину. Если нам встретилось ребро, ведущее в уже посещенную вершину - перенаправим его в новую компоненту и обойдем ее рекурсивно. После того, как мы прошли по ребру в новую вершину и вернулись обратно, тоже перенаправим его в новую компоненту. В итоге каждое ребро получится использовать повторно, если мы дойдем до всех компонент. Если компонента содержит хотя бы одно ребро, из нее можно перейти к следующей. Если в первую очередь перебирать только компоненты с ребрами, мы пройдем по ним по всем и по неравенству (m >= k -1) нам хватит ребер для посещения изолированных вершин.

Если степень вершины 1 равна нулю, мы не можем начать обход, пока не перенаправим в нее какое-нибудь ребро. После этого мы пройдем по этому ребру и выкинем его вместе с вершиной 1 из графа, так как больше использовать это ребро не сможем. Если выбранное ребро - мост, то мы получим в итоге k компонент связности и m - 1 ребро. Если не мост - k - 1 компоненту связности и m - 1 ребро. В первом случае условие m >= k - 1 превращается в условие m >= k. Во втором - m >= k - 1. Поэтому если не все ребра мосты, нужно брать не мост. Если все - мосты, нужно отсоединять ребро от вершины степени >= 2, чтобы не прийти в начальную ситуацию с нулевой степенью первой вершины. Если такой вершины не найдется, то легко показать, что нет решения.