The plates must touch the edge of the table, so their centers must lie on the circle with radius R - r (see the figure).

| 1 | 2 | 3 | 4 | |
| {1} | - | 1 | 1 | 1 |
| {1, 2} | 2 | 1 | 1 | 1 |
| {3, 1, 2} | 3 | 3 | 1 | 3 |
| {3, 1, 2, 4} | 3 | 3 | 1 | 3 |
 .
. by binary search (if the set was previously sorted). But there is more effective way of check in O(n). Note that if initially the points (xi, yi) were sorted, say, by x-coordinate in increasing order and in case of equal x by y, then the points of the form (2xc - xi, 2yc - yi) will be sorted in the reverse order. The order doesn't depend on the center (xc, yc). So we can check the points (2xc - xi, 2yc - yi) in the order of sorting moving a pointer in the sorted array (xi, yi).
by binary search (if the set was previously sorted). But there is more effective way of check in O(n). Note that if initially the points (xi, yi) were sorted, say, by x-coordinate in increasing order and in case of equal x by y, then the points of the form (2xc - xi, 2yc - yi) will be sorted in the reverse order. The order doesn't depend on the center (xc, yc). So we can check the points (2xc - xi, 2yc - yi) in the order of sorting moving a pointer in the sorted array (xi, yi).In conclusion, a couple of words about the difficulty order in the problemset must be said. Difficulty of a problem is subjective. Especially if we need to compare a problem with idea and nearly without implementation and implementation without idea. As a result, different participants form different preference lists (russian). I can't deny that the order chosen during preparation of the contest appeared to be inadequate with the number of solutions for the problems, and it surely can be not liked by someone personally. Nevertheless, I want to say a couple of words in its support. Namely, about principles we have used to choose it.









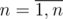 . Choose maximum among left-hand sides and minimum among right-hand sides and obtain an inequality in the form
. Choose maximum among left-hand sides and minimum among right-hand sides and obtain an inequality in the form 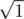 ,
, 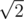 ,
, 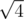 ,
, 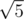 , and so on, i.e. the roots of integers, that can be represented as
, and so on, i.e. the roots of integers, that can be represented as 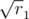 ,
, 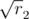 , ... In some cases we can take first
, ... In some cases we can take first 
