| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 164 |
| 1 | maomao90 | 164 |
| 3 | Um_nik | 163 |
| 4 | atcoder_official | 160 |
| 5 | -is-this-fft- | 158 |
| 6 | adamant | 157 |
| 6 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 8 | nor | 154 |
| 10 | djm03178 | 153 |
I am trying to solve this problem,I need your helps ;)
Is any idea to solve it,without 2d Trees? or what kind of 2d Trees should I use,that dont use O(n*m) memory,and update,query as much fast as it possible(like a logNlogM)
P.S I was reading material about fenwik tree,but it needs O(n*m) memory(sorry for my poor english )
think it up yourself
Probably he alredy tried if he asks for help?
Compress the pairs into numbers 1..X (UTFG compressing coordinates), then it's a classic LIS in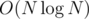
.Is wrong. At least for this operator (which, in fact, is not actually a comparison operator, so it technically isn't an increasing sequence because the term "increasing" remains undefined; it's actually a pair of LIS with common indices in 2 sequences). Well, an obvious extension to compressed 2D segment trees works, and I found an answer on Stack Overflow about it.
Thanksss, I GOT IT :)
告訴我怎麼解決問題?...
lol,I was thinking about numbering this pairs,but it seems it is incorrect :\
No, you can't compare 2 pairs (x1, y1) and (x2, y2) if x1 < x2 and y1 > y2. As far as I know, there is no way to solve this without 2D tree. Using set from C++ can simplify the implementation for this problem.
Yeah, I found out already. The problem is that I didn't read beyond "pair (a,b) is less than (c,d) if" because there is just one comparison operator on pairs.
. Oh I am wrong
can you explain what UTFG compressing coordinates is? I googled it but couldnt find anything.
http://lmgtfy.com/?q=utfg
One of the first page results: Urban Dictionary entry.
Need help again,if you can please tell my idea to solve this problem without 2d trees :\
A solution without trees was explained by Xellos up here.
And is wrong. More specifically, is wrong for the inequalities from the problem statement.
The explanation you linked from stack overflow, on the other hand, doesn't need an implementation of 2d trees and is correct.
My accepted code on SPOJ has 55 lines.
I think flashmt is right. I think you can use range tree which is a 2d tree :D
Notice that when you call update for fenwick you just update O((logN)d) nodes. If any node is not updated then it's value is zero. So you dont need O(NM) memory at all. O(M(logN)d) is enough.
PS: d means dimension
How would you remember the nodes to avoid O(N2) memory? The most obvious way to store Fenwick trees this way is using a map instead of a vector, but that adds a nasty factor of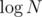
to the complexity.
Hash tables would be more usefull. So we can get rid of that O(logN)
While introducing a large constant. So much win...
We are not dealing with that huge constant. It is much more better then red-black trees in current realistic world limits too.
So, you're saying that we use a hashmap and still aren't dealing with the huge constant that it involves because... magic?
Im just saying that constant is not huge but obviously exists.
Here, it would appear that inserts have only about twice better performance for hashmap than map in C++, while fetches are much faster. And we still need to do a lot of inserts.
If you want to convince me, you'd need to provide a better argument than that you're saying, because I'm saying hashmap is a bad idea here and if anything then quicksort on subFenwick trees (1D) with many accessed elements and bubblesort on those with few (~5?) is faster.
Well, i dont care about convincing you. From my point of view twice faster hash table is tolerable.
Did you get AC on that problem ? (if not and you're still satisfied, then it isn't a good attitude for competitive programming :D)
It's SPOJ and SPOJ is slow, if map is a factor of 20 and hashmap is a factor of 10 then it's just a question of getting TLE with 6 or 3 seconds...
Also: how hash always works.
We can avoid this by preprocessing. Let's simulate all the queries to find out for each value of x, which values of y we will need to access.
I realize that we can find these values, but there is still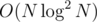
of them in total and we still need to sort them or map them or something. How else would you determine that query q1 and q2 both access the same vertex (x, y)?
Quicksorting (map and hashmap are both slow IRL) all y for all x would probably be enough to pass this on any fast online judge (I'd comfortably go code it if it was CF), but SPOJ isn't fast in any way, that's why I'm doubting stuff so much.
That's exactly what I did for this problem on SPOJ. Since we break N(logN)2 values into N different lists of x, the sorting part runs quite fast. After we get all y sorted for all x, when processing a query (x, y), we only need to find the actual index of y once for each of logN x values (by binary search) so it would cost O(N(logN)2) in total.