How can i solve this problem http://acm.timus.ru/problem.aspx?space=1&num=1103 ? I can think in an approach O(n^4), that's far from enough..... Basically i have N points and i want to draw a circle with 3 points on the edge, (N-3)/2 points inside and (N-3)/2 points outside of the circle. What are the points on the edge?
→ Обратите внимание
До соревнования
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
09:19:02
Зарегистрироваться »
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
09:19:02
Зарегистрироваться »
*есть доп. регистрация
→ Трансляции
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 4 | atcoder_official | 161 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 156 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
→ Найти пользователя
→ Прямой эфир
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 23.11.2024 08:16:00 (g1).
Десктопная версия, переключиться на мобильную.
При поддержке
Списки пользователей


| Название |
|---|










for each point on plane do a binary search, if radii is too big more points will be inside. contraints are such for each point we can keep points in order of their distance. N^2 + NlogN
Are you assuming that one of the points is a center? Why? The binary search doesn't guarantee that there will be exactly 3 points on the border, how to deal with this?
It is not hard to prove that we can draw such circle through any 2 points. This fact leads to evident O(n2) solution.
And if all the points are collinear? Assuming there is a solution, i don't understand why i can choose any 2 points.
It is true only if there is no 3 point on the same line and no 4 points on the same circle.
Here O(n) solution link
Basicly short version what I learned: 1) Answer always exists. 2) Take any segment on convex hull. Sort remaining points by angle making with this segment. Answer exactly in the middle.
of course other two points are vertices that make up this segment
Just try to 1e6 time choose three random points. And find count points in circle in O(n) time. Profit! P.S.: this solution get AC. Realy!
Let's fix one point (O) and assume it is on edge of circle. Make inversion with center O. What happens with our circle then? Circle edge becomes a line, which doesn't contain O. Inside and outside parts of circle (except O) become two parts of plane, created by line.
So we have n - 1 points (except O, we don't count it anymore), no 3 are on one line (because before inversion no 4 are on one line or on one circle), n isn't divisible by 2. We need to find a line, that divides our points in two groups of same size. Let's take points with biggest x coordinate. From such points let's take points with biggest y coordinate. Let's call it A. Then sort our points by polar angle around A and take (n - 1) / 2-th of them (B).
So, O, A', B' is answer, where A' is inverse of A, B' is inverse of B.
Complexity is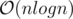 or even
or even 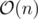 if you find median without sorting. There can be some precision problems, though.
if you find median without sorting. There can be some precision problems, though.
By the way, it looks like there is some trash at the end of third test.
Sorry for my bad English.
I am very sorry, double post.