pedromnasc's blog

Timus 1103. Pencils and Circles
By pedromnasc, 10 years ago, In English

How can i solve this problem http://acm.timus.ru/problem.aspx?space=1&num=1103 ? I can think in an approach O(n^4), that's far from enough..... Basically i have N points and i want to draw a circle with 3 points on the edge, (N-3)/2 points inside and (N-3)/2 points outside of the circle. What are the points on the edge?

  • Vote: I like it
  • +17
  • Vote: I do not like it

»
10 years ago, # |
  Vote: I like it 0 Vote: I do not like it

for each point on plane do a binary search, if radii is too big more points will be inside. contraints are such for each point we can keep points in order of their distance. N^2 + NlogN

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it +5 Vote: I do not like it

    Are you assuming that one of the points is a center? Why? The binary search doesn't guarantee that there will be exactly 3 points on the border, how to deal with this?

    → Reply
»
10 years ago, # |
  Vote: I like it +8 Vote: I do not like it

It is not hard to prove that we can draw such circle through any 2 points. This fact leads to evident O(n2) solution.

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    And if all the points are collinear? Assuming there is a solution, i don't understand why i can choose any 2 points.

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it +8 Vote: I do not like it

      It is true only if there is no 3 point on the same line and no 4 points on the same circle.

      → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it +8 Vote: I do not like it 
      There are no three pencils staying in one line
      → Reply
»
10 years ago, # |
← Rev. 4   Vote: I like it +13 Vote: I do not like it

Here O(n) solution link

Basicly short version what I learned: 1) Answer always exists. 2) Take any segment on convex hull. Sort remaining points by angle making with this segment. Answer exactly in the middle.

of course other two points are vertices that make up this segment

→ Reply
»
10 years ago, # |
  Vote: I like it +8 Vote: I do not like it

Just try to 1e6 time choose three random points. And find count points in circle in O(n) time. Profit! P.S.: this solution get AC. Realy!

→ Reply
»
10 years ago, # |
← Rev. 4   Vote: I like it +13 Vote: I do not like it

Let's fix one point (O) and assume it is on edge of circle. Make inversion with center O. What happens with our circle then? Circle edge becomes a line, which doesn't contain O. Inside and outside parts of circle (except O) become two parts of plane, created by line.

So we have n - 1 points (except O, we don't count it anymore), no 3 are on one line (because before inversion no 4 are on one line or on one circle), n isn't divisible by 2. We need to find a line, that divides our points in two groups of same size. Let's take points with biggest x coordinate. From such points let's take points with biggest y coordinate. Let's call it A. Then sort our points by polar angle around A and take (n - 1) / 2-th of them (B).

So, O, A', B' is answer, where A' is inverse of A, B' is inverse of B.

Complexity is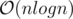 or even 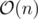if you find median without sorting. There can be some precision problems, though.

By the way, it looks like there is some trash at the end of third test.

Sorry for my bad English.

→ Reply
»
10 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

I am very sorry, double post.

→ Reply