I recently read “Still Simpler Static Level Ancestors by Torben Hagerup” describing how to process a rooted tree in O(n) time/space to be able to answer online level ancestor queries in O(1). I would like to explain it here. Thank you to camc for proof-reading & giving feedback.
background/warmup
Prerequisites: ladder decomposition: https://codeforces.me/blog/entry/71567?#comment-559299, and <O(n),O(1)> offline level ancestor https://codeforces.me/blog/entry/52062?#comment-360824
First, to define a level ancestor query: For a node u, and integer k, let LA(u, k) = the node k edges “up” from u. Formally a node v such that:
- v is an ancestor of u
distance(u, v) = k(distance here is number of edges)
For example LA(u, 0) = u; LA(u, 1) = u’s parent
Now the slowest part of ladder decomposition is the O(n log n) binary lifting. Everything else is O(n). So the approach will be to swap out the binary lifting part for something else which is O(n).
We can do the following, and it will still be O(n):
- Store the answers to O(n) level ancestor queries of our choosing (answered offline during the initial build)
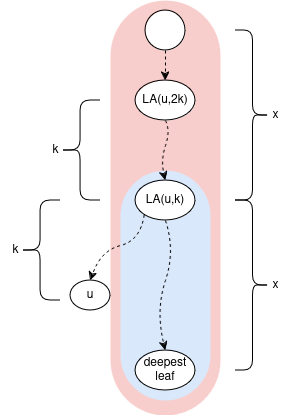
- Normally in ladder decomposition,
length(ladder) = 2 * length(vertical path). But we can change this tolength(ladder) = c * length(vertical path)for any constantc(of course the smaller the better).
The key observation about ladders: Given any node u and integer k (0 <= k <= depth[u] / 2): The ladder which contains LA(u, k) also contains LA(u, 2*k); or generally LA(u, c*k) when we extend the vertical paths by the multiple of c.
the magic sequence
Let’s take a detour to the following sequence a(i) = (i & -i) = 1 << __builtin_ctz(i) for i >= 1 https://oeis.org/A006519
1 2 1 4 1 2 1 8 1 2 1 4 1 2 1 16 1 2 1 4 1 2 1 8 1 2 1 4 1 2 1 32 1 2 1 4 1 2 1 …
Observe: for every value 2^k, it shows up first at index 2^k (1-based), then every 2^(k+1)-th index afterwards.
Q: Given index i >=1, and some value 2^k, I can move left or right. What’s the minimum steps I need to travel to get to the nearest value of 2^k?
A: at most 2^k steps. The worst case is I start at a(i) = 2^l > 2^k, e.g. exactly in the middle of the previous, and next occurrence of 2^k
the algorithm
Let’s do a 2n-1 euler tour; let the i’th node be euler_tour[i]; i >= 1. Let’s calculate an array jump[i] = LA(euler_tour[i], a(i)) offline, upfront.
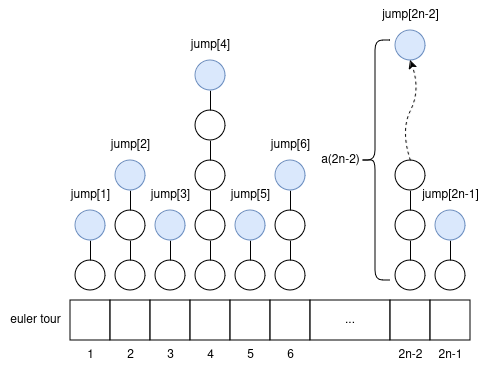
how to use the “jump” array to handle queries?
Let node u, and integer k be a query. We can know i = u’s index in the euler tour (it can show up multiple times; any index will work).
key idea: We want to move either left, right in the euler tour to find some “close”-ish index j with a “big” jump upwards. But not too big: we want to stay in the subtree of LA(u,k). Then we use the ladder containing jump[j] to get to LA(u,k). The rest of the blog will be the all math behind this.
It turns out we want to find closest index j such that 2*a(j) <= k < 4*a(j). Intuition: we move roughly k/2 steps away in the euler tour to get to a node with an upwards jump of size roughly k/2.
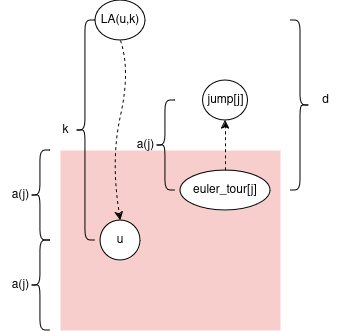
Note if we move to j: abs(depth[euler_tour[i]] - depth[euler_tour[j]]) <= abs(i - j) <= a(j)
Note we’re not creating a ladder of length c*a(i) starting from every node because that sums to c*(a(1)+a(2)+...+a(2n-1)) = O(nlogn). Rather it’s a vertical path decomposition (sum of lengths is exactly n), and each vertical path is extended upwards to c*x its original length into a ladder (sum of lengths <= c*n)
finding smallest c for ladders to be long enough
Let’s prove some bounds on d = depth[euler_tour[j]] - depth[LA(u,k)]
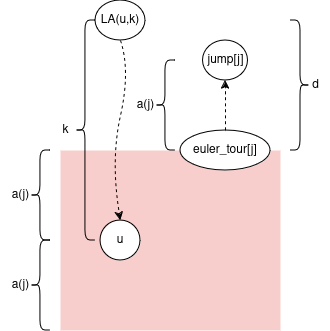
Note 2*a(j) <= k from earlier. So a(j) = 2*a(j) - a(j) <= k - a(j) <= d. This implies jump[j] stays in the subtree of LA(u,k).
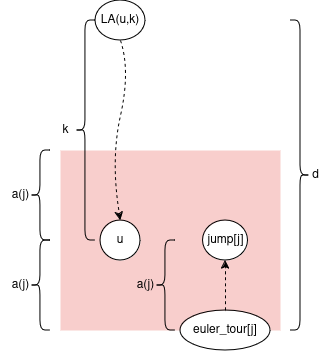
Note k < 4*a(j) from earlier. So d <= a(j) + k < a(j) + 4*a(j) = 5*a(j)
Remember, we can choose a constant c such that length(ladder) = c * length(vertical path). Now let’s figure out the smallest c such that the ladder containing jump[j] will also contain LA(u,k):
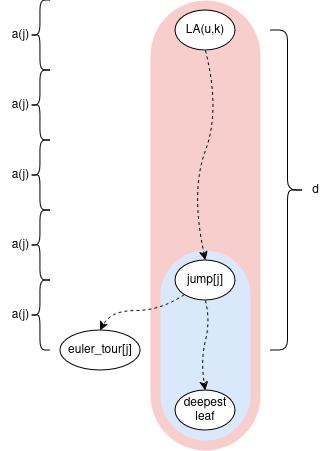
if we choose c=5 then length(ladder) = 5 * length(vertical path) >= 5 * a(j) > d

I mean that constant factor kinda sucks :( Well, at least we’ve shown a way to do the almighty, all-powerful theoretical O(n)O(1) level ancestor, all hail to the almighty. If thou is tempted by method of 4 russians, thou shall receive eternal punishment
here’s a submission with everything discussed so far: https://judge.yosupo.jp/submission/194335
a cool thing
Here’s some intuition for why we chose the sequence a(i): It contains arbitrarily large jumps which appear regularly, sparsely. Sound familiar to any algorithm you know? It feels like linear jump pointers https://codeforces.me/blog/entry/74847. Let’s look at the jump sizes for each depth:
1,1,3,1,1,3,7,1,1,3,1,1,3,7,15,1,1,3,...
Map x -> (x+1)/2 and you get https://oeis.org/A182105 . https://oeis.org/A006519 is kinda like the in-order traversal of a complete binary tree, and https://oeis.org/A182105 is like the post-order traversal.
improving the constant factor
Let’s introduce a constant kappa (kappa >= 2).
Instead of calculating jump[i] as LA(euler_tour[i], a(i)), calculate it as LA(euler_tour[i], (kappa-1) * a(i))
Let node u, and integer k be a query. We want to find nearest j such that kappa*a(j) <= k < 2*kappa*a(j)
Then you can bound d like: (kappa-1) * a(j) <= d < (2 * kappa + 1) * a(j)
And you can show c >= (2 * kappa + 1) / (kappa - 1)
The catch is when k < kappa, you need to calculate LA(u,k) naively (or maybe store them).
The initial explanation is for kappa = 2 btw
submission with kappa: https://judge.yosupo.jp/submission/194336











Hi, I revisited this, and was able to improve the constant factor a tiny bit:
currently, the blog describes an algorithm where you choose
kappa(kappa >=2) and it gives an algorithm where ladders need to be extended(2*kappa+1)/(kappa-1)of their original length.Now, I found an improved version where you still choose
kappa(kappa>=1 now) and you only need to extend ladders(2*kappa+1)/kappaof their original lengththe idea is to calculate
jump[i]instead asLA(v, KAPPA*a(i))wherevis the deepest node out ofeuler_tour[j],euler_tour[j+1], ...,euler_tour[j+a(i)]https://judge.yosupo.jp/submission/242264
hi, ok last time hopefully
I had another idea which allows ladders to be only twice their original length:
scratch my above idea: it appears to be correct, but it's complicated, and it requires 2 DFS's. Instead do exactly as in the blog with
kappa=3, but now store 2 jump pointers (offline,up front):jump[i] = {LA(euler_tour[i], 2 * a(i)), LA(euler_tour[i], 4 * a(i))}now in the query, do exactly as in the blog, except out of the 2 jump pointers, choose the higher one which is still in the subtree of
LA(u,k)https://judge.yosupo.jp/submission/242808
rough proof sketch why
c=2makes ladders long enough:jump[j].firstwill always be in the subtree ofLA(u,k)jump[j].secondsometimes will be outside the subtree ofLA(u,k)Now
jump[j].first's ladder sometimes will not containLA(u,k). This happens whendepth[jump[j].first] - 2a(j) >= depth[LA(u,k)]. So let's consider this case.In this case:
depth[jump[j].second] = depth[jump[j].first] - 2a(j) >= depth[LA(u,k)]sojump[j].secondwill be in the subtree ofLA(u,k)depth[LA(u,k)] >= depth[u] - 6a(j) > depth[euler_tour[j]] - 8a(j)sojump[j].second's ladder will be long enough to containLA(u,k)