У меня есть решение задачи G с Codeforces Round #900 (Div.3), которое работает за $$$O(n \cdot (log(A) + log(n)) + q \cdot log(A))$$$ по времени.
Я заметил, что никто не упоминал это решение, поэтому я попробую его объяснить.
Из-за того, что чтобы посчитать побитовое ИЛИ на пути нужно $$$O(log(n))$$$ операций, суммарно нам потребуется $$$O(n \cdot log(A) + q \cdot log(A) \cdot log(n))$$$ операций. Наша задача состоит в том, чтобы как-то избавиться от множителя $$$O(log(n))$$$ и научиться вычислять побитовое ИЛИ на пути за $$$O(1)$$$. Чтобы это сделать необходимо:
Во-первых, давайте предподсчитаем для каждой вершины какие предки её поменяют. Сделаем это при помощи динамики. Какая вершина может поменять наше значение ИЛИ? Или наш непосредственный родитель, или тот, кто поменял родителя. Почему? Потому что если поднимемся один раз, то окажемся в родителе и добавим его биты себе и только те, кто поменяли родителя возможно смогут поменять и нас. Существует не более $$$O(log(A))$$$ вершин, которые могут поменять значение вершины на пути к корню.
Во-вторых, давайте запомним запросы в вершинах. То есть для каждой вершины мы запомним список запросов, где эта вершина участвует. В этом списке будем хранить другую вершину из запроса и индекс запроса. Да, будем отвечать в оффлайне.
В-третьих, как теперь вычисляется ИЛИ? Пусть $$$(x, y)$$$ — пара вершин из запроса, $$$l$$$ = $$$LCA(x, y)$$$, и $$$z$$$ — промежуточная вершина на пути от $$$x$$$ к $$$l$$$. Давайте предположим, что мы поднимаемся из $$$x$$$. Мы уже предпосчитали все вершины $$$z$$$ для данного $$$x$$$, которые могут её поменять. Так что можно легко посчитать ИЛИ на пути $$$path(x, z)$$$. $$$path(z, y)$$$ разбивается на $$$path(z, l)$$$ и $$$path(l, y)$$$. Мы можем вычислить $$$path(l, y)$$$ с помощью бинарных подъёмов. Мы так можем сделать потому что мы это делаем один раз для всех возможных вершин $$$z$$$. Но что с $$$path(z, l)$$$? Тут уже нельзя использовать бинарные подъёмы, чтобы посчитать ИЛИ.
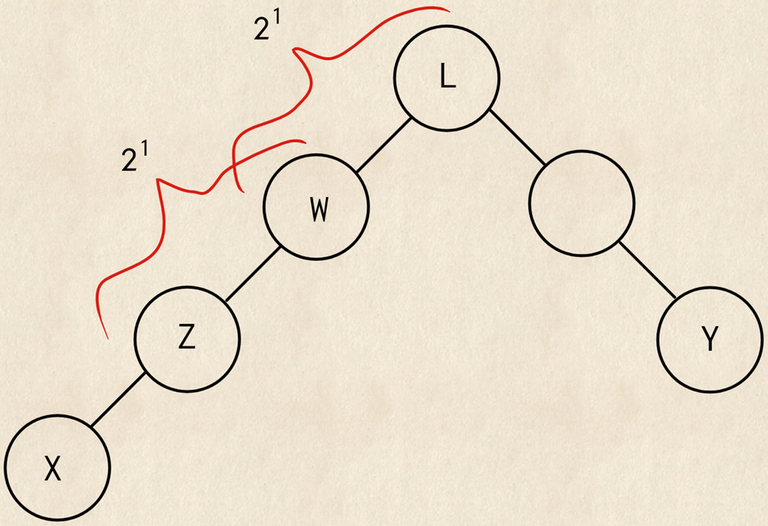
Давайте воспользуемся $$$\bf{идемпотентностью}$$$ функции ИЛИ. Это значит $$$ИЛИ(ИЛИ(a, b), ИЛИ(b, c)) = ИЛИ(a, b, c)$$$. Эта идея очень схожа с идеей Разреженной таблицы. Мы уже до этого считали что-то вроде $$$sum$$$_$$$or[i][j]$$$ $$$=$$$ побитовое ИЛИ на пути к корню из $$$i$$$ длиной length $$$2^j$$$. Так, ИЛИ на пути $$$path(z, l)$$$ разбивается на $$$sum$$$_$$$or[z][p]$$$ | $$$sum$$$_$$$or[w][p]$$$ для какой-то вершины $$$w$$$ и показателя степень двойки $$$p$$$ таких, что $$$2^p \le dist(w, l) < 2^{(p+1)}$$$.
- Но как же узнать вершину $$$w$$$? Для этого мы и запоминали все запросы. Теперь нам нужно поддерживать путь от корня до $$$x$$$ чтобы быстро находить вершину $$$w$$$. Теперь мы можем вычислить побитовое ИЛИ на пути dfs'а за $$$O(1)$$$ кодом вроде этого:
Смотрите это решение и авторское.
В результате нашей работы, это решение имеет сложность по времени $$$O((n + q) \cdot (log(A) + log(n)))$$$











If you still have any questions regarding this solution — feel free to ask me here!
Amazing! I would never have thought that it could be solved so effectively!
Actually, your solution is not the fastest. You are taking 3rd place right now.
All solutions sorted by its runtime
magnus.hegdahl solved it in 2 times faster than you