I have a solution for problem G from Codeforces Round #900 (Div.3) that has $$$O(n \cdot (log(A) + log(n)) + q \cdot log(A))$$$ time complexity.

I am noticed that nobody mentioned this solution, so I will try to explain it.

So, because in order to calculate bitwise OR on a path we need $$$O(log(n))$$$ time complexity it takes in total $$$O(n \cdot log(A) + q \cdot log(A) \cdot log(n))$$$. Our task is to somehow get rid of this $$$O(log(n))$$$ factor and calculate bitwise OR on a path in $$$O(1)$$$. In order to do this we will do the following:

• First, let's precalculate for each vertex which vertices change it. We do this using DP. What vertex could change our OR value? Either the parent one, or the one, that changed our parent. Why? Because if we lift one edge up, then we will include bits from our parent and only those, who changed it may change us. There are no more than $$$O(log(A))$$$ vertices that can change given vertex on its path to root.

• Second, let's stash queries into nodes. That is for each vertex we will remember the list of queries where this vertex participates. This list includes the other vertex in query and its index. Yes, we will answer the queries offline.

• Third, how do we calculate OR now? Let $$$(x, y)$$$ be a pair of vertices from query, $$$l$$$ = $$$LCA(x, y)$$$, and $$$z$$$ an intermediate vertex on path from $$$x$$$ to $$$l$$$. Let's assume we lift from vertex $$$x$$$. We already precalculated all vertices $$$z$$$ for given $$$x$$$ that will change it. So we can calculte OR on $$$path(x, z)$$$ easily. $$$path(z, y)$$$ splits into $$$path(z, l)$$$ and $$$path(l, y)$$$. We can calculate $$$path(l, y)$$$ using binary lifts. We can do this becase it is done only once for all possible $$$z$$$ vertices. But what for $$$path(z, l)$$$? We can't use binary lifts to calculate it anymore.

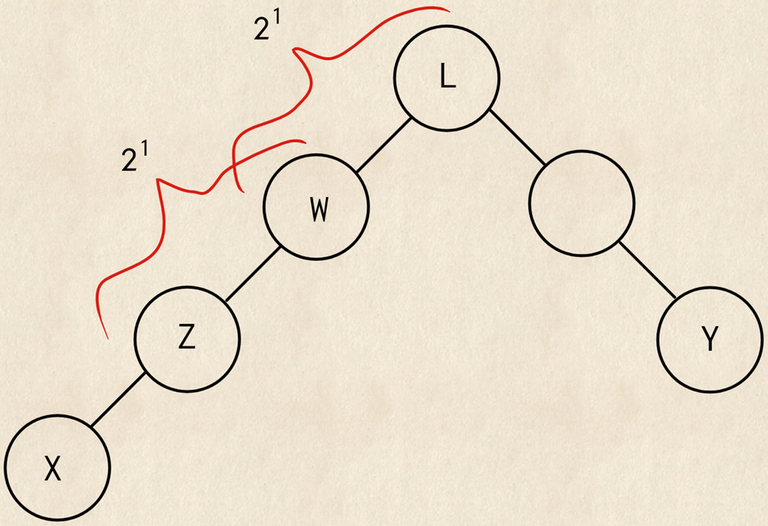
• Let's use $$$\bf{idempotence}$$$ of OR function. That is $$$OR(OR(a, b), OR(b, c)) = OR(a, b, c)$$$. This idea is very simular to the one we use in Sparse table data structure. We already calculated something like $$$sum$$$_$$$or[i][j]$$$ $$$=$$$ bitwise OR on path from $$$i$$$ of length $$$2^j$$$. So, OR of $$$path(z, l)$$$ breaks down into $$$sum$$$_$$$or[z][p]$$$ | $$$sum$$$_$$$or[w][p]$$$ for some vertex $$$w$$$ and power $$$p$$$ such that $$$2^p \le dist(w, l) < 2^{(p+1)}$$$.

• But how do we get the vertex $$$w$$$? For this, we stashed all queries. Now we need to maintain a path from root to $$$x$$$ in order to quickly find vertex $$$w$$$. Now we can calculate bitwise OR on dfs path in $$$O(1)$$$ using code like this:

    auto or_last = [&](int cur, int len) {
      if (len == 0) {
        return arr[cur];
      }
      int p = __lg(len);
      int diff = len - (1 << p);
      return sor[p][cur] | sor[p][tour[inds[cur] - diff]];
    };

See this solution and the intended one.

As the result of our work, this solution has time complexity $$$O((n + q) \cdot (log(A) + log(n)))$$$