bin_2u's blog

Trilogy Innovations OA Questions and Intuitions
By bin_2u, 16 months ago, In English

Hello everyone,

Yesterday,Trilogy Innovations OA was held. There were 4 Questions and the time limit was 120 minutes. I am attaching all the questions. It would be really helpful, If we discuss the intuitions and Approaches to the problems. I felt Problems were Quite Interesting.


Change permutation
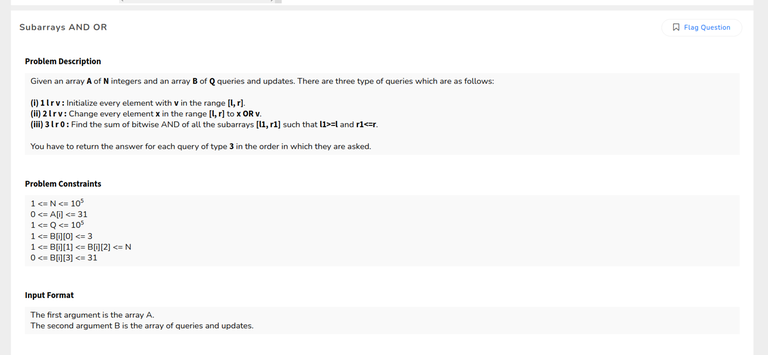
SubArray - AND - OR
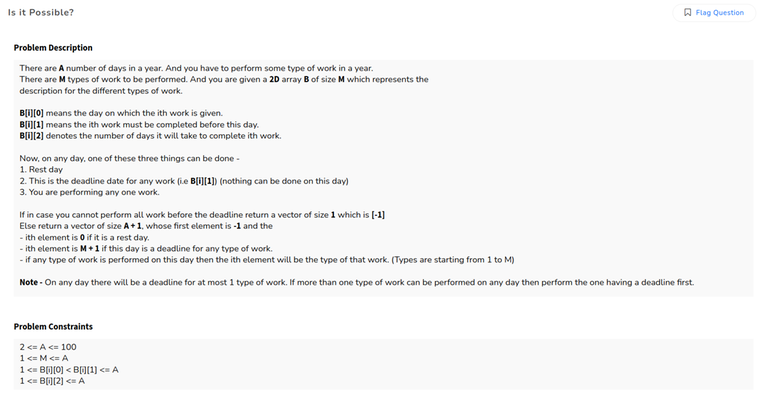
Is It possible
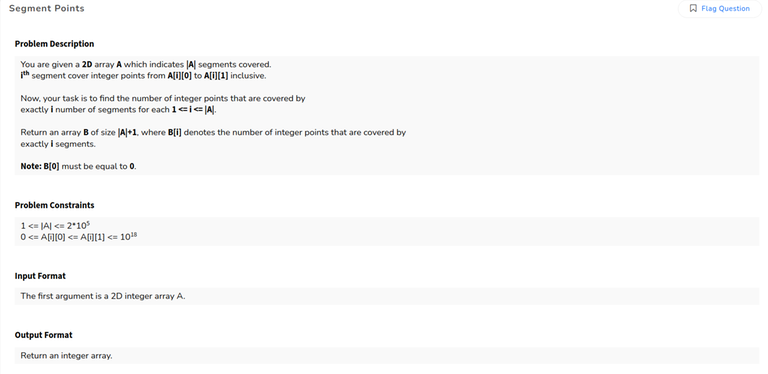
Segment points

I personally felt first 2 problems were a bit challenging.

Thank You,

  • Vote: I like it
  • +24
  • Vote: I do not like it

Comments Comments (15)
| Write comment?
»
16 months ago, # |
  Vote: I like it +1 Vote: I do not like it

Thanks for sharing...!!

→ Reply
»
16 months ago, # |
  Vote: I like it +1 Vote: I do not like it

In 4th problem i used difference array concept on map what did you do?

→ Reply
»
16 months ago, # |
  Vote: I like it +9 Vote: I do not like it

Solution sketches

A, write permutation as product of cycles, note that number of moves to change to identity is M = sum(c_i — 1), and doing a swap will change this value by +/- 1.

B, do each bit separately, now suppose A[i] <= 1. segment tree, state S[i..j] stores the answer to query type-3 and length of prefix/suffix of ones. operations are set=0, set=1, or nothing.

C, greedy, earlier due date has higher priority

D, sweep line (iterate over each interval-endpoint in sorted order)

→ Reply
  • »
    »
    16 months ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    Can u explain more on the solution for B ?

    → Reply
  • »
    »
    16 months ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    In problem B how would you combine the answers of multiple intervals while querying??

    → Reply
»
16 months ago, # |
  Vote: I like it -7 Vote: I do not like it

Can I code these problems in any coding platform?

→ Reply
»
16 months ago, # |
← Rev. 2   Vote: I like it +16 Vote: I do not like it

2nd problem can be solved using lazy propagation. It's given that A[i] <= 31, which means we only need to consider first 5 bits. so let's solve the problem bit by bit. for any bit the array A will be a binary array. To find the number of subarrays in a range L, R satisfying the 3rd query, we only need to consider the subarrays having only 1's. This can be solved using segment trees. we just need to make a node to store the number of prefix 1's, suffix 1's, length of the range, and the number of subarrays having only 1's. The main task is to make a merge function for merging the left and right nodes of a segment tree. This would be easy if you are comfortable with segment trees. To solve the 1st query, you only need to assign a particular value to a given range which is a current bit of a given number that can be either 0 or 1. For the second query, think if a current bit is 0, this won't affect the range because x OR 0 gives you x. So update the range, only if a current bit is 1. To answer the 3rd query, iterate from 0th bit to the 4th bit and calculate the number of subarrays in a range having only 1's for a current bit. For a particular bit 'b', your answer will be (1 << b) * (the number of subarrays with only 1's). You need to add this answer for every bit ranging from 0 to 4.

→ Reply
  • »
    »
    16 months ago, # ^ |
      Vote: I like it +14 Vote: I do not like it

    Very nice. Love and support from Nepal.

    → Reply
  • »
    »
    16 months ago, # ^ |
      Vote: I like it +8 Vote: I do not like it

    Either I am missing something terribly simple or you might have left out a case for the query of 3rd type for this segment tree for some bit 'b'.

    Consider this query of the third type: 3 2 6 0

    There isn't a node that will cover exactly this range and the nodes that will return their answers will be [2-2], [3-4], and [5-6](I recommend looking at the segment tree I have drawn).

    Wouldn't we need the following?

    • suffix 1's in [2-2]
    • prefix 1's in [3-4]
    • suffix 1's in [2-4]
    • prefix 1's in [5-6]

    Of course, prefix 1's and suffix 1's in [2-2], [3-4] and [5-6] would be maintained in the segment tree but, what about the suffix 1's in [2-4]? Let me know if I am missing something or if you intended this will be handled in your solution, when you said:
    "...The main task is to make a merge function for merging the left and right nodes of a segment tree. This would be easy if you are comfortable with segment trees..."

    → Reply
    • »
      »
      »
      16 months ago, # ^ |
        Vote: I like it +1 Vote: I do not like it

      Merging the nodes (1, 2) and (3, 4) will handle the case.

      → Reply
      • »
        »
        »
        »
        16 months ago, # ^ |
          Vote: I like it +3 Vote: I do not like it

        So, we can just use values of the [1-4] node to get the suffix 1's for [2-4]. Now I understand, thanks for responding!

        → Reply
  • »
    »
    16 months ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    are you converting the number array entirely to a binary array? can you please explain your approach with a small example for all 3 queries?

    → Reply
    • »
      »
      »
      16 months ago, # ^ |
      ← Rev. 2   Vote: I like it 0 Vote: I do not like it
      • Let's say we have an array = [3 2 1 7].
      • If we consider only first 3 bits then our new 2d array will like:
      • bit[0] = [1 0 1 1]
      • bit[1] = [1 1 0 1]
      • bit[2] = [0 0 0 1]
      • Assume a 1st query i.e, change [0th index to 2nd index] by 4, it will only affect the bit[2] array. So, our updated arrays will be:
      • bit[0] = [1 0 1 1]
      • bit[1] = [1 1 0 1]
      • bit[2] = [1 1 1 1]
      • For a 3rd query (1st index to 3rd index), our answer would be: (1 << 0) * (3) + (1 << 1) * (2) + (1 << 2) * 6.
      → Reply
»
15 months ago, # |
  Vote: I like it 0 Vote: I do not like it

Codeforces has a similar question to the third one https://codeforces.me/contest/978/problem/G

→ Reply