Я умею обрабатывать запросы типа "изменить значение в вершине", посчитать что-то на пути.
А как изменять значение на ребре? Есть идея хранить в вершине вес ребра из вершины в ее левого сына (в Splay tree). Но тогда возникает проблема с изменением корня дерева: при реверсе ребер, значения в вершинах будут неправильными, и придется как-то пропихивать веса в левого сына.
Подскажите, пожалуйста, как правильно хранить и изменять вес ребра в Link-cut tree?
Upd. Обновил картинку
Upd2. Только что нашел: http://www.cs.princeton.edu/~rwerneck/docs/TW07.pdf
The obvious implementation of the ST-tree interface is to store with each node its value and a pointer to its parent. This supports link, cut, parent and findcost in constant time, but evert, findroot, findmin and addcost must traverse the entire path to the root. Despite the linear-time worst case, this representation might be good enough for graphs with small diameter, given its simplicity. We tested two variants of this implementation, lin-v and lin-e; the former associates costs with vertices, the latter with edges. Both store values at vertices, but lin-e interprets such a value as the cost of the arc to the parent (the values must be moved during evert).











Если честно, то я не знаю, что такое Link-cut Tree, так что, возможно, мое предложение окажется полнейшим бредом.
Первое что пришло в голову: Почему бы не заменить ребро (a, b) вершиной, связанной с вершинами a и b? Тогда в этой вершине можно хранить информацию о ребре.
Обычно в похожих ситуациях помогает хранить вес ребра из вершины в её родителя — такое ребро ровно одно и проблем должно быть меньше.
Да, но опять же, как быть с изменением корня? Тогда родитель поменяется
Wouldn't it be sufficient to just store the value of an edge in the bottom vertex of that edge? It's just 1 value per edge, and the value of any path that crosses that edge doesn't have that vertex as its topmost one (which can just be subtracted, since there's no other such vertex) will also include the value of that vertex.
As I understood, the main problem is with 'expose' request as it rebuilds the tree and changes 'topmost vertex of an edge'.
Oh, so that's why the link-cut tree was specifically mentioned...
In that case, I don't know. I try to avoid the use of such structures — I try to keep my thinking simple. Maybe you could use some clever sqrt-stuff?
Of course the problem I am trying to solve does not require link-cut structure, it is about the lightest edge on a path queries and it can be solved much more easier. But as I understand Link-Cut tree solves almost all problems about queries on tree, that's why I want to use Link-Cut here.
Can you pleas tell how to solve lightest edge on a path queries ??
I think what he means is that it's easy to solve it offline, if you don't have update queries. You can use static heavy-light decomposition or something like centroid decomposition.
Oh, could you help me to solve lighest edge on a path queries in a dynamic graph?? ...
Can you please provide some link which will help me solve this problem
You have it right here: Use a link-cut tree. There's several resources for that in this thread alone
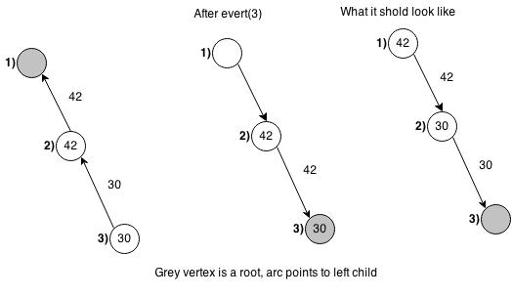
accesswill not change the parent-child relation of any two nodes in the represented tree, if I'm not mistaken. Since the node depths don't change,accessshould not even change the left/right relation inside an auxiliary tree (although the parent-child relation might change there). So we could identify an edge with its bottom vertex in the represented tree, which happens to be always to be always to the right of it in the auxiliary trees (except when the endpoints are not on the same preferred path, in which case we get the off-by-one situation Xellos mentioned)Yes, access does not change the parent-children relations, but I am talking about evert operation, which swaps left and right children inside a splay tree. Take a look at updated picture
An edge connects two nodes in the represented tree, one of which is the parent and one of which is the child. If you write the edge value into the child you can just do normal range queries in the auxiliary tree. The splay tree operations have little to do with that, they are just a means to compute range aggregations on the path.
So don't think about it in terms of left/right in the auxiliary trees. Two neighboring nodes in the represented tree might not even be directly connected in the auxiliary tree.
As I understood, we have a rooted tree, so we can clearly define vertex values and we don't care about auxiliary tree changes at all.
For example we want to represent such a tree:
Initially all vertices are in different trees. And how to perform link(2, 3, 25) query? I don't know where to write 25
You can only link tree roots: http://en.wikipedia.org/?title=Link/cut_tree#Link. Those don't have an edge value yet, so you can just write the 25 into the newly linked node (in this case, node 3) and the invariant is still fulfilled.
Trees are never restructured if you use link/cut.
2 and 3 both are roots. So you mean that it does not matter where to put 25 and if I put 25 in 2 it will be ok too?
No, you need to put it into the 3. Just put the edge value into the bottom vertex always. It's always possible because every node only has one parent edge.
What do you mean by bottom vertex? For example how can I find bottom vertex in link(1, 2, 10) query?
Or it is possible only if we know all link/cut queries to hang a tree?
By bottom vertex of an edge, I mean the deeper one of the vertices that the edge connects.
link(x,y)assumes thatxis the root of a tree in the represented forest. Thereforexhas no parent edge and if you connect it toy,xwill be the deeper of the two nodes, so it can hold the edge value.Ok, but we need to somehow push the value from a node, because the node must be empty to link it.
Your example doesn't make sense. 1 is not a root so you
link(1,3,20)is not a valid operation. You can only link root nodes. I meantioned this a few times now in this thread, but you seem to skip over most of what I write.You could do
link(2,4,20orlink(2,3,20)orlink(4,1,20)orlink(4,2,20)without problems.With that misunderstanding out of the way, I hope it becomes now clear that your "problematic case" can just not occur in practice.
Maybe you should read the Wikipedia article so we at least agree on a common vocabulary.
1 is not a root, but I can change the root, by evert operation.
The root can be changed by evert(v), which reverses all arcs on the path from v to the previous root.
http://www.cs.princeton.edu/~rwerneck/docs/TW07.pdf
Take a look at 2. Data Structures -> ST-trees
Okay, I didn't know about
evert. However, have a look at page 82 of the document you sent me:"We call the splay-based implementation used in our experiments ST-V. Although it has costs on vertices, it can also represent costs on edges as long as
evertis never called. Supportingevertwith costs on edges requires maintaining additional nodes to represent the edges explicitly. Our implementation of this variant, ST-E, uses ST-V as the underlying data structure."Also have a look at the original ST-Tree paper. They use a reverse bit in the splay tree data structure to implement
evert. They also maintain edge costs.Когда я это писал, я сделал для каждого ребра фиктивную вершину и поместил ее между двумя концами этого ребра. После этого все становится понятно. Выглядит как костыль, но Burunduk1 и PavelKunyavskiy сказали, что не знают ничего более красивого, и у меня есть основания им верить.
Кто-нибудь может поделиться информацией про link-cut tree с реализацией через декартово дерево за O(N log^2 N)?