Div2-A
Заводим массив used на 100 элементов и заполняем его таким образом: used[i] = 1, если хотя бы один из однокашников Алексея претендует на часть (i, i + 1). Далее проходимся циклом от l1 до r1 - 1 и находим количество тех i, для которых used[i] = 0. Это и будет ответом.
Эту задачу можно решать и за O(nlogn), используя сортировку событий или просто сортировку и линейное решение далее. Такое решение будет находить требуемую величину сразу для всех отрезков.
Div2-B
Посчитаем, сколько раз по L мы можем взять, не превысив N. Это количество равно 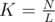 .
.
Тогда, если R·K ≥ N, будем увеличивать какое-то из K чисел на 1, в какой-то момент у нас получится в сумме N, так в итоге будет больше. Значит ответ — YES.
В обратном случае, если мы возьмем не больше K чисел, то их сумма меньше N. Если взять больше K чисел, то сумма будет больше N. Значит ответ — NO.
Сложность ответа на 1 запрос: O(1).
Div1-A/Div2-C
Разложим все данные n чисел на простые множители. Теперь нам нужно решить задачу отдельно по каждому простому, а потом перемножить ответы для различных простых. Количество способов разбить pk, где p — простое, на n множителей равно C(k + n - 1, n - 1) (Это можно получить методом шаров и перегородок, подробнее здесь, выбрать combinatorics). Таким образом, получаем решение за 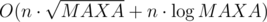 .
.
Div1-B/Div2-D
Пусть для начала n + 1 = p — простое. Докажем по индукции, что в этом случае ответ —  . При p = 3 — очевидно. Пусть это равенство доказано для p, а q — следующее простое. Тогда ответ для q — это ответ для p плюс q - p одинаковых слагаемых вида
. При p = 3 — очевидно. Пусть это равенство доказано для p, а q — следующее простое. Тогда ответ для q — это ответ для p плюс q - p одинаковых слагаемых вида 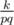 , то есть
, то есть  , что и требовалось доказать.
, что и требовалось доказать.
Далее, воспользовавшись тем, что между любыми соседними простыми числами, не превосходящими 109, разница не более нескольких сотен, находим ответ, как ответ для наибольшего (явно проверяем числа на простоту за корень) не превосходящего простого плюс 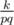 . Отсюда же замечаем, что в ответе знаменатель это 2pq (или его делитель), что влазит в
. Отсюда же замечаем, что в ответе знаменатель это 2pq (или его делитель), что влазит в int64.
Div1-C/Div2-E
Запишем все вершины в порядке обхода dfs'а, тогда потомки одной вершины образуют подотрезок. Запомним также для каждой вершины расстояние от нее до корня level[v].
Заведем два дерева отрезков (ДО). При запросе на изменения в первом ДО добавим на отрезке, соответствующем потомкам вершины v, x + level[v]·k, а во втором ДО на том же отрезке добавим k.
Тогда, если обозначим первое ДО как st1, второе ДО как st2, то при запросе второго типа в вершине v нужно вывести st1.get(v) - st2.get(v) * level[v].
Сложность: O(qlogn)
Вместо дерева отрезков можно использовать другие структуры данных, поддерживающие добавление на отрезке и запрос в одном элементе. Также в комментариях приведен способ несколько другой реализации: http://codeforces.me/blog/entry/10961#comment-162286
Также существует решение с Heavy-Light декомпозицией.
Div1-D
Заметим полезный факт: если взять все перестановки длины k, то сумма количеств инверсий в них будет равна 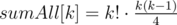 . Доказывается он очень просто: если в перестановке p для каждого i заменим pi на k + 1 - pi, то сумма количеств инверсий p и новой перестановки будет равна
. Доказывается он очень просто: если в перестановке p для каждого i заменим pi на k + 1 - pi, то сумма количеств инверсий p и новой перестановки будет равна 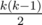 , и при этом наше преобразование является биекцией.
, и при этом наше преобразование является биекцией.
Далее будем считать, что все перестановки на числах от 0 до n - 1, а не от 1 до n, как в условии. Ясно, что в этом нет никакой разницы.
Пойдем по перестановке с начала. Какие перестановки бывают меньше данной?
- Те, у которых первое число меньше, чем p0. Пусть первое число a < p0, тогда в каждой такой перестановке a инверсий вида (первый элемент, еще какой-то элемент). То есть всего во всех перестановках с первым числом a их a·(n - 1)!. Кроме того, есть инверсии среди элементов, не содержащих первый. Их суммарно sumAll[n - 1]. Тогда суммарно по всем a получаем инверсий:
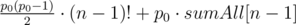 .
. - Перестановки, которые начинаются на p0: Во-первых, нужно учесть кол-во инверсий, начинающихся в начале. Их cnt·p0, где cnt — количество перестановок, начинающихся на p0 и не больших данной. Во-вторых, нужно учесть инверсии "не в начале". Но это такая же задача! Единственное исключение — меньше числа p1 может быть доступно не p1 чисел, а меньше на 1, если p1 > p0. Отсюда получаем решение: итерируемся с начала, запоминаем в дереве Фенвика числа, которые уже использованы, далее решаем такую же задачу, но считаем что первое число это pi - (кол-во уже использованных чисел, меньших чем pi).
Осталось посчитать количество перестановок, не больших чем суффикс данной и начинающихся также. Это можно легко пересчитывать, если двигаться не вперед, а назад. В таком случае нужно делать то же самое, но минимальное число считать равным количеству уже использованных чисел, меньше данного.
Div1-E
Опишем алгоритм, а потом поймем, почему он делает то, что нужно.
Заведем для каждого простого числа список полуинтервалов. Изначально для каждого простого pi, имеющегося в инпуте, положим туда [0;ai). У всех остальных простых оставим список пустым.
Далее, будем итерироваться по всем простым в порядке убывания. Пусть текущее простое p. Если в его списке есть полуинтервал вида [x;y), $x < k, y > k$, разделим его на 2 полуинтервала [x;k) и [k;y).
Далее для каждого полуинтервала [x;y), x ≥ k (на самом деле, x > k не бывает) добавим к ответу для p величину y - x, а для полуинтервалов y ≤ k добавим к списку каждого из простых делителей числа p - 1 полуинтервал [x + 1, y + 1). В случае, если p - 1 делится на больше чем первую степень какого-то простого, нужно добавить такой отрезок несколько раз.
После этого нужно провести операцию "объединения со смещением" для всех простых, у которых изменился список. Если в одном списке существуют 2 полуинтервала [x, y), [z, t) при y ≥ z > x, то их нужно заменить на 1 полуинтервал [x, y + t - z) (т.е добавить t - z к концу первого из них). Далее переходим к следующему (меньшему) p.
Почему это работает? Вспомним сперва, что происходит с числом n при одной итерации взятия φ. Для любого p, которое входит хотя бы 1 раз в разложение числа n, n делится на p и умножается на p - 1 (или, что тоже самое, на все простые числа p - 1 в соответсвующих степенях).
Теперь поймем, что полуинтервалы, которые мы поддерживали для чисел — это то, после каких по счету итераций число содержало в себе данный простой множитель. На большие простые меньшие никак не влияют, поэтому их можно рассматривать раньше. Если после i-ой итерации число содержало простой множитель p, то после i + 1-й оно будет содержать простые делители p - 1, поэтому мы именно таким образом передаем отрезки. Итерация с номером k — последняя, поэтому полуинтервал [k, x) означает, что после k-ой итерации останется степень x - k данного простого. Отсюда понятно, почему нужно объединять отрезки со смещением, как описано выше.
Почему это работает быстро?
Потому что мы предподсчитали решетом за линию минимальный делитель каждого числа и раскладываем число на простые за кол-во простых в нем. (На самом деле это делать не обязательно)
Потому что для каждого простого отрезков одновременно, очевидно, не более чем log(MAXP) = 20, ибо для каждого [a, b) выполняется a ≤ log(MAXP) + 1. Если чуть подумать, то их не более чем половина от этого, ибо 2 отрезка не начинаются в подряд идущих числах. Экспериментально, их не более 6.
Несколько другой подход к этой задаче описан в комментариях: http://codeforces.me/blog/entry/10961#comment-162236
Авторы не уверены, что в разборе все решения написаны понятно, поэтому любые вопросы по нему приветствуются!
Пост был восстановлен из кэша google, формулы были оформлены заново, поэтому, если видите ошибку в них, пожалуйста, пишите мне в личку.











Can you explain more deeply your Div2-D solution??? I do not understand your function. Did you make it approximately? Sorry if I am annoyed.I'm just newbie and I really want to learn new thing. :)
No. It's an exact solution. We divide all the summands of the given sum to groups of equal summands. If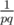 `. Notice that
`. Notice that 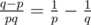 . Then we sum all of them.
. Then we sum all of them. 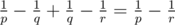
pandqare consecutive prime numbers then there areq - peach of them equal toCan someone explain DIV1-A problem more deeply?
" Now we should solve the problem for every prime independently and multiply these answers "
why it's true ?
Great problem set.. though editorial could be even better. :)
I am getting wrong answer for Div2-C. Could someone explain me why? Here's my submission — http://codeforces.me/contest/397/submission/12231922
limits are pretty wrong note that a prime divisor can even be 1e9 ! u r only checking up to 1e4 also the fact array limit is not enough i think u can check my submition http://codeforces.me/contest/396/submission/12250925
Hello Everyone, can someone please explain me solution of Div.2 E with more details?
I'll be grateful if someone'll, any help is appreciated!
More exactly: how does it work & why does it work?