На всякий случай, ссылка на анонс и обсуждение.
А теперь разбор.
A div 2: 378A - Игра с кубиком
Заведем три счетчика: для побед каждого из игроков и для ничьи. Переберем все варианты, как можно выбросить кубик — их всего 6 штук. Для каждого варианта определим, кто выиграет, или будет ли ничья, и прибавим единицу к соответствующему счетчику.
B div 2: 378B - Полуфиналы
Можно немного подумать и понять, что достаточно рассмотреть крайние случаи k = 0 и 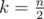 . Все остальные случаи будут средними между этими двумя.
. Все остальные случаи будут средними между этими двумя.
В случае k = 0 мы должны выбрать n максимальных элементов из двух посорченных списков, это можно сделать, например, двумя указателями. А в случае 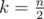 отметим первых
отметим первых  спортсменов в каждом списке.
спортсменов в каждом списке.
A div 1 / C div 2: 377A - Лабиринт
Запустим поиск в ширину или в глубину из любой свободной клетки. Так как лабиринт связный, этот поиск обойдет все s свободных клеток. Однако мы прервем этот поиск на том моменте, когда он посетит s - k свободных клеток. Очевидно, эти s - k клеток образуют связную область. Оставшиеся k клеток просто превратим в стены.
Претесты проходило также решение, каждым ходом превращающее в стену ту клетку, у которой меньше всего соседей. Это неверно, например, на следующем тесте:
....
.#..
..##
..##
У левой верхней клетки не большее число соседей, чем у любой другой, однако ее нельзя превращать в стену.
B div 1 / D div 2: 377B - Подготовка к соревнованию
Очевидно, что время исправления всех багов — функция монотонная: если можем сделать все за какое-то время, то сможем и за большее, поэтому будем искать ответ бинарным поиском. Так что пусть мы знаем время, за которое надо исправить все баги. Проверим, можно ли это сделать.
Вначале отсортируем баги по сложности, а студентов по скиллу (это можно сделать один раз вне бинарного поиска). Посмотрим на самый сложный баг. Кто мог бы его исправить? Очевидно, его могут исправить те студенты, чей скилл не меньше сложности бага. Поместим всех таких студентов в очередь с приоритетами (в которой будет сортировка по стоимости студентов) и выберем оттуда самого дешевого. Так как мы проверяем время t, то этот студент должен пофиксить t самых сложных багов (он точно может их пофиксить). Отметим это, и перейдем к рассмотрению следующего непофикшенного бага. Снова поместим всех студентов, которые могли бы его исправить (по студентам надо проходиться параллельно с багами), в очередь с приоритетами и выберем самого дешевого. И так далее. Если в какой-то момент оказалось, что текущий баг не может исправить ни один студент (очередь с приоритетами пуста), значит время t не подходит в бинарном поиске. Если мы не уложились в требуемое количество зачетов — тоже не подходит. Иначе мы найдем нужное расписание.
C div 1 / E div 2: 377C - Captains Mode
Есть несколько наблюдений, после которых задача становится очень простой. Первое наблюдение — пикать надо всегда самого сильного героя. А вот про баны ничего такого сказать нельзя, в разных ситуациях могут потребоваться самые разные баны. Самое важное наблюдение, которое поможет решить задачу — то, что рассматривать следует только m сильнейших героев. Действительно, при любой игре, где будут пикаться самые сильные герои в каждый момент времени, никакой герой, кроме первых m, не может быть пикнут вообще никогда. Значит, и банить их никогда не надо. И рассматривать тоже.
В итоге у нас остается в худшем случае 20 героев, а, значит, можно решить задачу динамикой по подмножествам: dpmask — разность между силами команд в ситуации, когда пикнуты либо забанены те и только те герои, чьи биты в маске установлены в единицу. Для переходов перебираем героя, которого команда, чья очередь хода, будет пикать или банить. Проще всего реализовать это с помощью рекурсии с сохранением. Ответ будет храниться в dp2m - 1.
К сожалению, мы неправильно оценили сложность этой задачи (несмотря на простое в реализации решение, придумать его, как выяснилось, было не так то и просто — стандартные 1500 баллов были бы лучше), и выставили неправильный TL (так что многие решения на C++ за m2·2m проходили — следовало опустить ограничение до одной секунды, а то и до 0.75 секунд). Так что если вы решили задачу за m2·2m, считайте, что вам повезло и что ваш вердикт — Time Limit Exceeded.
Почему можно писать это за m·2m? Потому что пропуск бана не имеет смысла: вместо этого можно забанить самого слабого героя из доступных — ведь его точно никто никогда не пикнет.
Здесь тоже были слабые претесты, поэтому можно было ломать тех, у кого в решении не было битмасок, чуть ли не любым большим случайным тестом.
D div 1: 377D - Разработка игры
Рассмотрим оптимальный ответ. Заметим, что каждый ответ характеризуется такими двумя числами L и R, что max{li} ≤ L, R ≤ min{ri}, и L ≤ vi ≤ R. Т.е., зная L и R, мы можем перебрать всех сотрудников и выбрать тех, что подходят под вышеперечисленные условия.
Нарисуем плоскость, по оси абсцисс которой будем откладывать параметр L, а по оси ординат — R. Если точка (L, R) на этой плоскости является оптимальным ответом, то сотрудники, которые входят в ответ, обязательно удовлетворяют соотношениям li ≤ L ≤ vi и vi ≤ R ≤ ri. Эта область представляет собой прямоугольник на плоскости. Так как нам надо найти максимальное количество сотрудников, мы должны отыскать такую точку (L, R), что она входит в как можно большее количество указанных прямоугольников.
Это уже совершенно стандартная задача, решающаяся с помощью сканирующей прямой по одной оси и дерева отрезков — по другой. Основная сложность — сведение к ней.
E div 1: 377E - Cookie Clicker
Для начала избавимся от вырожденных строений: оставим для каждого vi только строение с наименьшим ci при этом vi. А также выбросим все строения, скорость которых меньше скорости самого быстрого строения с ci = 0.
Также довольно очевидно, что имеет смысл в каждый момент времени использовать только самое быстрое строение. И если мы будем в оптимальном ответе когда-нибудь использовать какое-либо строение, то купить его надо сразу же, как только появятся на это деньги (я буду называть печенья деньгами). И сразу же начать использовать.
Представим себе плоскость (x, y), где по оси абсцисс будем откладывать время, а по оси ординат — деньги. Будем поддерживать график y = f(x) функции "максимальное количество денег, которое можно заработать за время x", добавляя на этот график поочередно по одному строению. Этот график представляет собой объединение отрезков прямых с угловыми коэффициентами vi, каждый из которых активен на некотором отрезке [xli, xri].
К примеру, в начале это просто прямая y = v1x, где v1 — скорость строения, которое можно купить за 0 рублей. Пусть следующее по скорости строение можно купить за c2 рублей. Найдем минимальную точку x02, график функции в которой больше или равен y = f(x02) ≥ c2, и купим это строение в момент времени x02. Тогда мы должны построить прямую y = y02 + v2x, где y02 = f(x02) - c2 — сколько денег останется после покупки. Итого у нас есть две прямых. До какого-то момента (причем не до x02, а немного дольше) выгоднее будет старая прямая, но так как v2 > v1, найдется момент времени (это ceil(x12), где x12 — точка пересечения двух прямых), когда выгоднее станет новая прямая. Теперь отрезков прямых в графике две.
Продолжим добавлять все строения таким образом. Отрезки прямых следует, как во всех задачах с выпуклой оболочкой, хранить в стеке и на каждом шаге отсекать те, которые уже не нужны (т.е. те, которые лежат в стеке после той, с которой было пересечение текущей добавляемой прямой). Обработав все строения, найдем минимальное время, за которое можно заработать S денег и выведем это число в ответ.
Если требуется еще и сказать, какие строения надо при этом использовать, надо для каждого отрезка хранить тот, из которого он был получен (т.е. тот, который использовался перед тем, как мы купили этот). Имея такой "массив предков", нетрудно восстановить ответ. Чтобы задача стала немного проще, мы убрали из финальной версии вывод сертификата.











B div 1 / D div 2: 377B - Подготовка к соревнованию Сложность авторского решения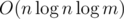 ?
?
D div 1: 377D - Разработка игры Наверное имелось ввиду max{li} ≤ L, R ≤ min{ri}.
Да. Но работает очень быстро. Даже на Java с ее автоупаковкой за 0.5 секунд заходит.
Исправил, спасибо.
Я писал с сетом и не прошло даже предтесты :(
Вместо такого:
Нужно юзать такое:
Так как первое даёт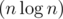 , а второе —
, а второе — 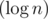
Понимаю, что это не основная мысль Вашего комментария, но все-таки в худшем случае и за O(1) амортизированно. Так что std::lower_bound на сете работает за O(n).
в худшем случае и за O(1) амортизированно. Так что std::lower_bound на сете работает за O(n).
it++для сета работает заIn problem C: "no hero except m strongest cannot be picked". I think there should be "no hero except m strongest can be picked".
Yeah. Probably there are lots of errors in my english translation.
In E we can use funny trick and add an artificial building with cost S and slope infinity and all we need to obtain a result is to check whether our current building's cost is equal to S, and if so, print the first moment we can buy it. This makes another solution a bit easier since we don't need any additional loop to obtaining result after processing all buildings.
Very nice problemset!
I think that the tag of problem E div1 should rather be geometry or convex hull than be DP ...
Div 1 C. Captains Mode.
Я не могу понять, как мы узнаем, по какому пути пойдет игра при двух стороная, каждая из которых хочет выиграть. В динамике, когда есть тоько одна сторона можно просто брать максимальное значение. Но что делать, когда одна сторона хочет банами уменьшить итоговое максимальное значение, а другая — увеличить?
Ну просто в одном случае берем минимум, а в другом максимум.
a
Thanks for the counterexample in Div2C.
In DIV1 what is s in s-k?
Total number of cells I guess.
total number of empty cells initially