Hi everybody! Tomorrow at 12:00 UTC there will be the third round of Yandex.Algorithm 2018. You can enter contest from the Algorithm main page.
This round is written by me with a great help of GlebsHP and everybody who was testing the round. While solving the problems, you will be helping some of my colleagues here at Yandex to deal with some practical (or not) situations. Good luck to everybody!
Enter the contest
UPD: Round is over! Congratulations to Merkurev, jcvb and Um_nik who got first three places in the standings.
The elimination stage is over and we can now find out who are the contestants that are going to compete in the Algorithm Finals in Saint Petersburg: elimination scoreboard.
There is also a round editorial (ENG only) available.
Good luck and see you later!












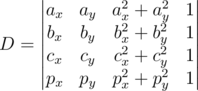
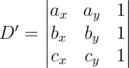
 using the geometric inversion transformation, but we will not discuss it since it's running time is about the same as the running time of a solution above.
using the geometric inversion transformation, but we will not discuss it since it's running time is about the same as the running time of a solution above. 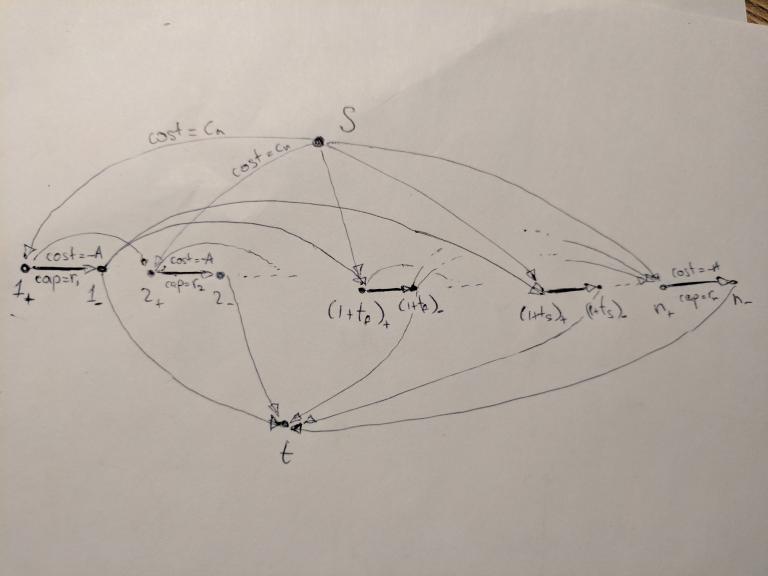

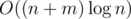 .
.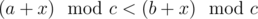 . It's easy to see that if we consider all residues modulo
. It's easy to see that if we consider all residues modulo 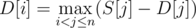 .
. 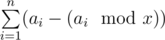 . Note that under the summation there is a number that is divisible by
. Note that under the summation there is a number that is divisible by 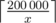 different terms in this sum. Let's calculate the value of a sum spending the operations proportional to the number of different terms in it.
different terms in this sum. Let's calculate the value of a sum spending the operations proportional to the number of different terms in it.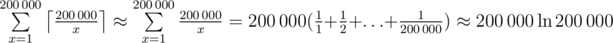 operations. It's useful to know that the sum inside brackets is called a harmonic series, and that its sum is very close to the natural logarithm of the number of terms (up to a constant factor in limit).
operations. It's useful to know that the sum inside brackets is called a harmonic series, and that its sum is very close to the natural logarithm of the number of terms (up to a constant factor in limit).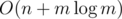 where
where 
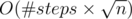 : all we need is to just simulate the process. Suppose we are now standing in number
: all we need is to just simulate the process. Suppose we are now standing in number  , then all divisors larger than
, then all divisors larger than  since our number can't infinitely increase (it can be shown that it can't move further than
since our number can't infinitely increase (it can be shown that it can't move further than 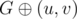 (here
(here  means inverting the specific edge, adding it or removing it). If
means inverting the specific edge, adding it or removing it). If 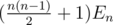 almost-Eulerian graphs: each Eulerian graph
almost-Eulerian graphs: each Eulerian graph 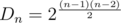 since there may be any possible set of edges between vertices
since there may be any possible set of edges between vertices 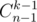 ways to choose
ways to choose 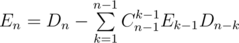 that leads us to an
that leads us to an 
