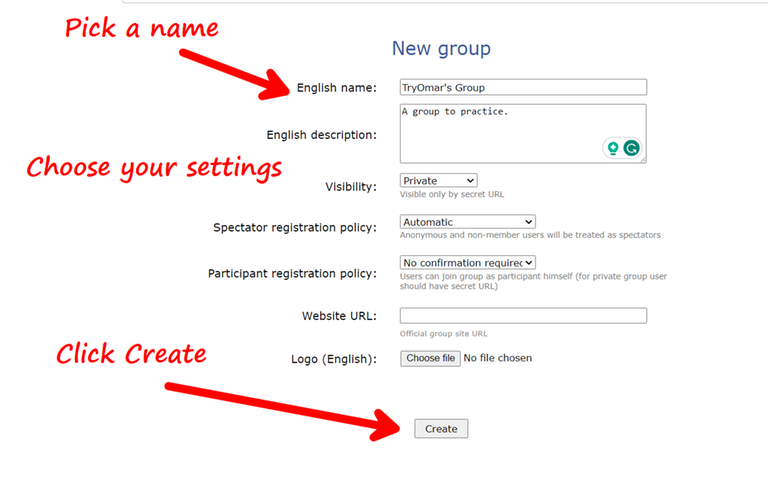
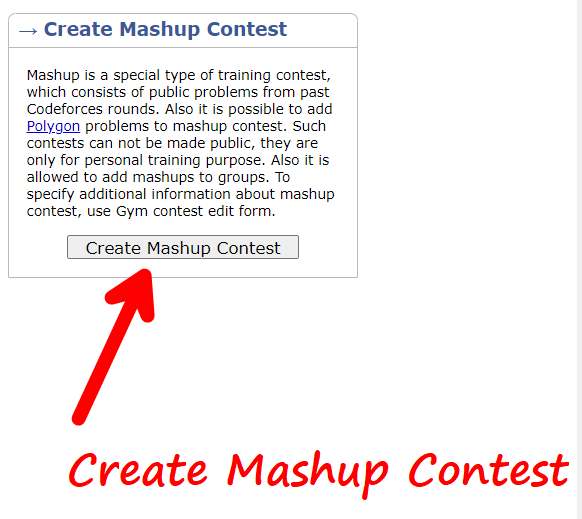
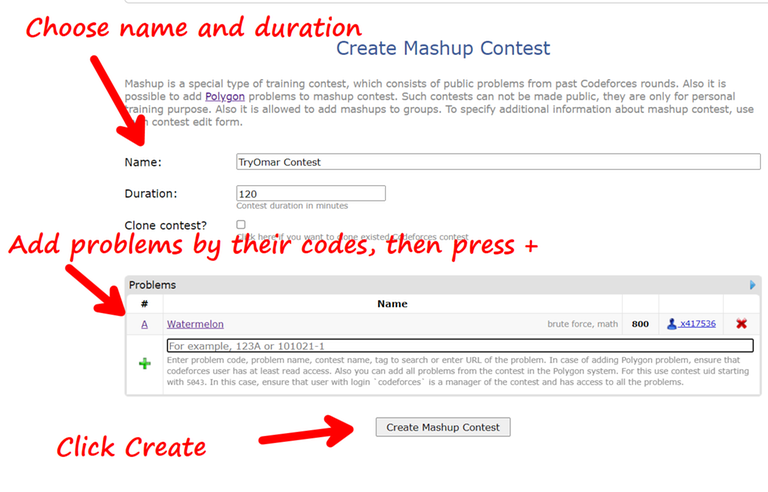
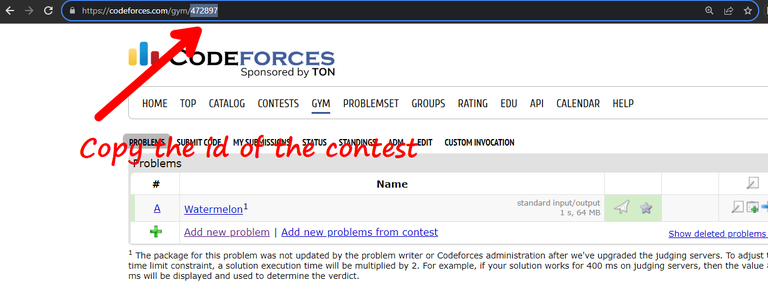
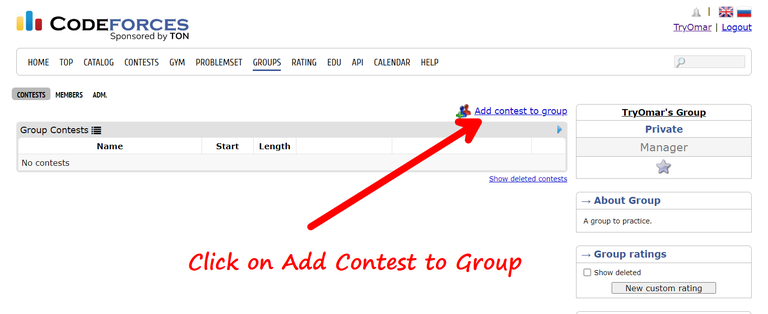
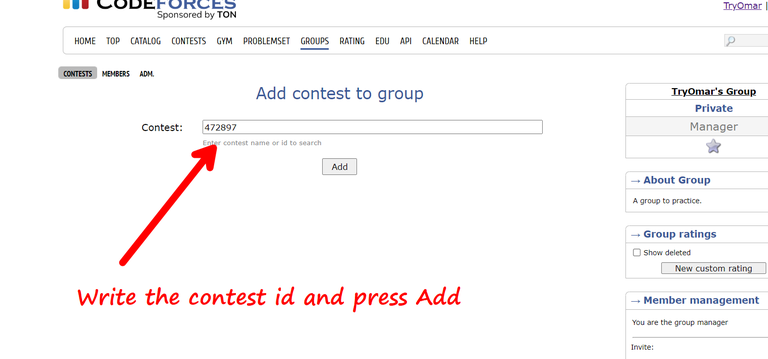
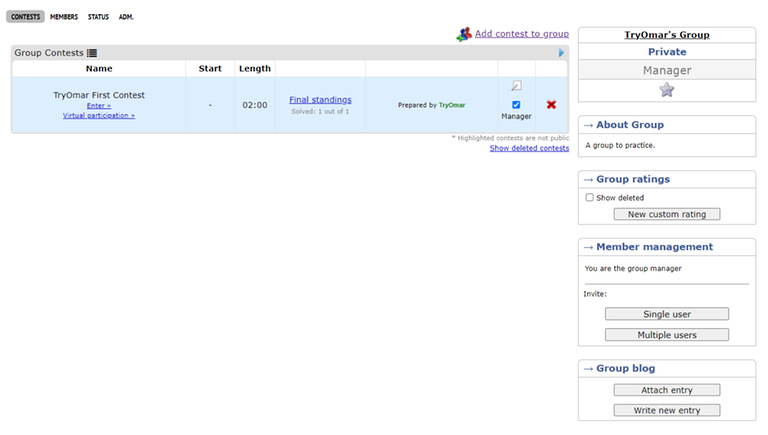
Ordered Sets in C++
In C++, ordered sets can be created using special code templates.
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
using namespace __gnu_pbds;
template<class T> using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
template<class T> using ordered_multiset = tree<T, null_type, less_equal<T>, rb_tree_tag, tree_order_statistics_node_update>;Two primary structures are introduced:
ordered_setmaintains sorted unique elements in ascending order usinglesscomparison.ordered_multisetallows duplicates using aless_equalcomparison, preserving the sorted order.
Fucntions
In addition to normal set operations, the ordered set supports:
order_of_key(k): Gives the count of elements smaller thank. — O(log n)find_by_order(k): Returns the iterator for thekth element (usek = 0for the first element). — O(log n)
Deletion in Multiset
To remove an element in a multiset, you must delete it using iterators:
ss.erase(ss.find_by_order(ss.order_of_key(x)));
Simple Usecase
#include <iostream>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
using namespace std;
using namespace __gnu_pbds;
template<class T> using ordered_multiset = tree<T, null_type, less_equal<T>, rb_tree_tag, tree_order_statistics_node_update>;
int main() {
// Declaration of ordered_multiset as 'ss'
ordered_multiset<int> ss;
// Inserting elements into 'ss'
ss.insert(5);
ss.insert(2);
ss.insert(7);
ss.insert(2); // Allows duplicates
ss.insert(1);
// Displaying elements
cout << "Elements in the ordered_multiset: ";
for (auto it : ss) { // 1 2 2 5 7
cout << it << " ";
}
cout << endl;
// Counting elements less than 5 using order_of_key
cout << "Elements less than 5: " << ss.order_of_key(5) << endl; // 3
// Deleting an element, e.g., deleting value 2
auto it = ss.find_by_order(ss.order_of_key(2)); // Find iterator to the element 2
if (it != ss.end()) {
ss.erase(it); // Erase the found element O(log n)
cout << "Element 2 removed from the ordered_multiset." << endl;
} else {
cout << "Element not found in the ordered_multiset." << endl;
}
return 0;
}Sorting Descending (or Equal)
This modification greater allows sorting elements in descending order for set or multiset.
template<class T> using ordered_set = tree<T, null_type, greater<T>, rb_tree_tag, tree_order_statistics_node_update>;
template<class T> using ordered_multiset = tree<T, null_type, greater_equal<T>, rb_tree_tag, tree_order_statistics_node_update>;Operator Overload
The custom comparison operator is used for handling duplicates within an ordered multiset. It ensures that duplicate elements are retained while maintaining the desired sorting order based on the specified comparison logic.
template<class T>
struct custom_compare {
bool operator()(const T& a, const T& b) const {
if (a == b) return true; // Keep duplicates
return a > b;
}
};
template<class T> using ordered_multiset = tree<T, null_type, custom_compare<T>, rb_tree_tag, tree_order_statistics_node_update>;You can modify the operator to sort based on anything you want, for example, based on the frequency of each element you would return fr[a] < fr[b];.
Also, you can check my article on sorting in normal sets/multisets here: Custom Sorting in Normal Sets/Multisets