The computer game is based on this task on UVa OJ.
Recently, I wrote some code to develop it. (Both Engish and Chinese version)
You can download the code here.
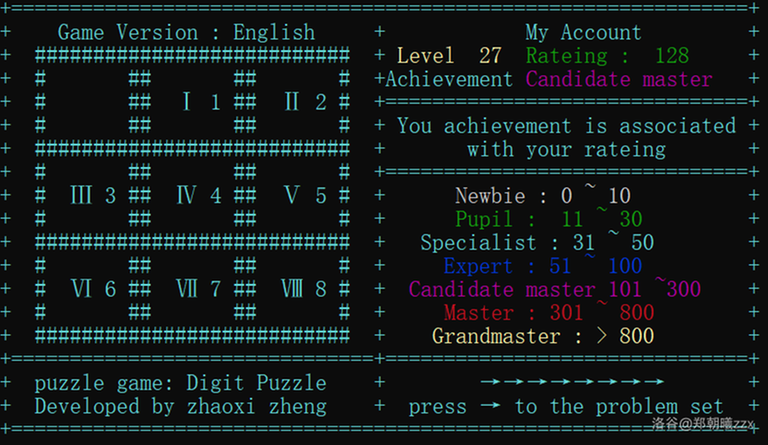
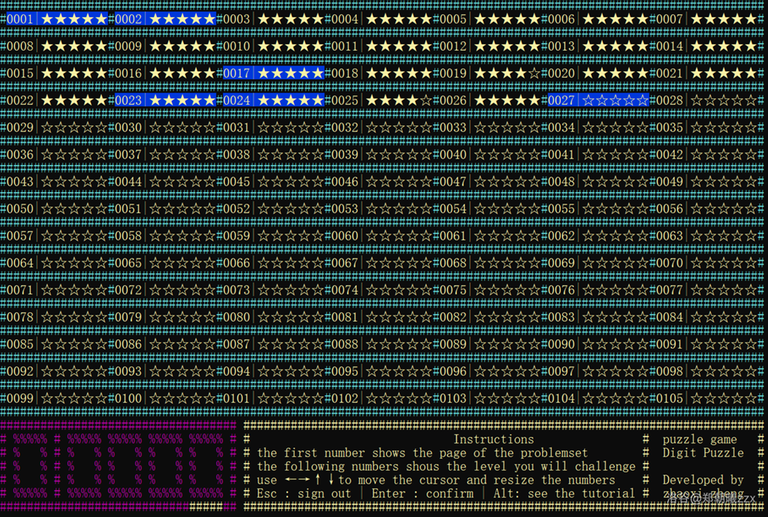
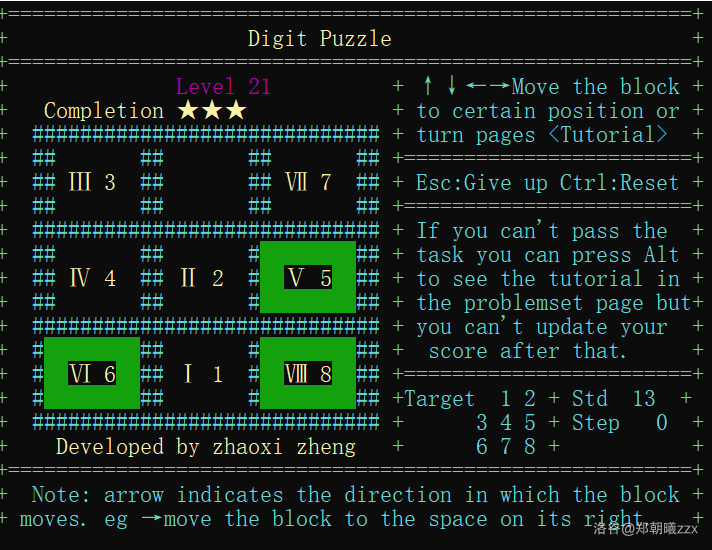
Game page display:
- Engish Version:
- Chinese Version:
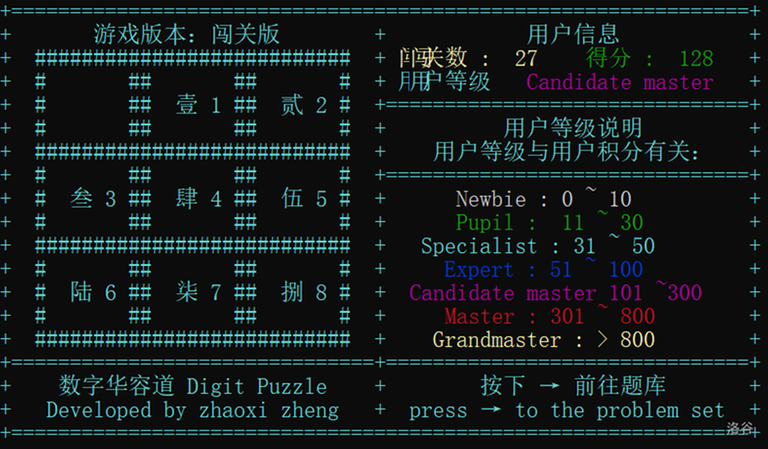
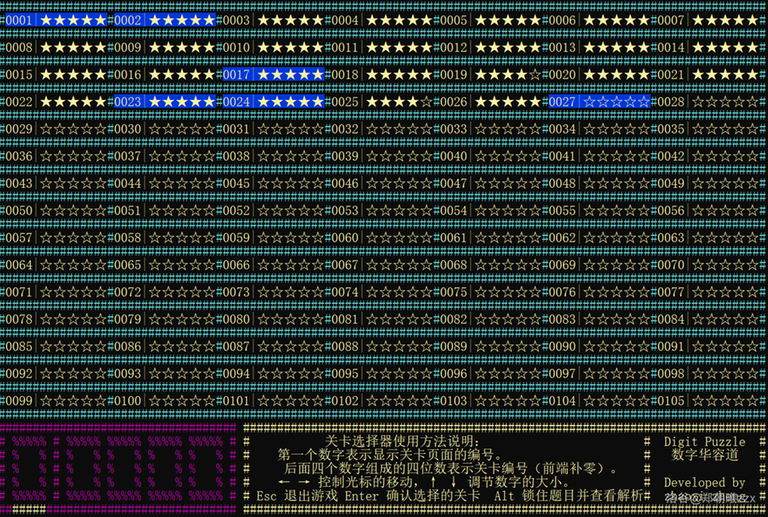
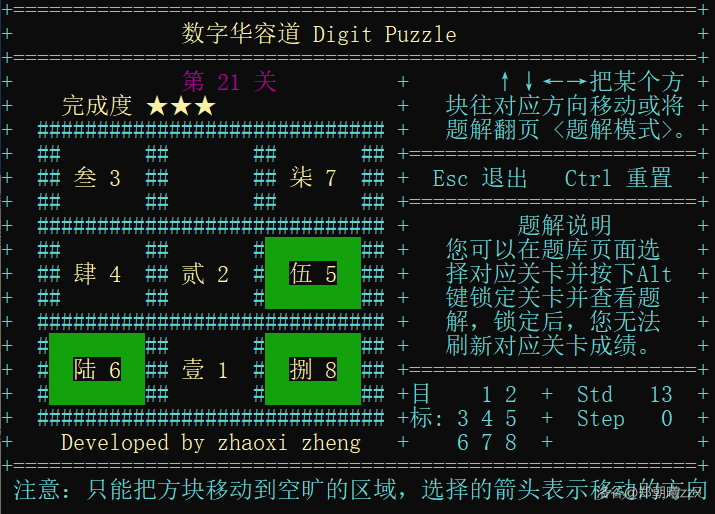
You are welcome to try it.
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3993 |
| 2 | jiangly | 3743 |
| 3 | orzdevinwang | 3707 |
| 4 | Radewoosh | 3627 |
| 5 | jqdai0815 | 3620 |
| 6 | Benq | 3564 |
| 7 | Kevin114514 | 3443 |
| 8 | ksun48 | 3434 |
| 9 | Rewinding | 3397 |
| 10 | Um_nik | 3396 |
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 155 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 10 | nor | 152 |
The computer game is based on this task on UVa OJ.
Recently, I wrote some code to develop it. (Both Engish and Chinese version)
You can download the code here.
Game page display:






You are welcome to try it.
Segment Tree is a useful data structure that can solve problems like RMQ in $$$O(n)$$$ build tree and $$$O(\log(n))$$$ for each query or update.
What can it query?
sum
maxinum / minium
gcd / lcm
other thing that can be push up
Lets use segment Tree to query the sum of an array.

Lets look at the example, the tree is just like many segments!
It's easy to find that the number on the bottom is the sum of the two numbers on it.
The $$$l$$$ and $$$r$$$ note the left endpoint and the right endpoint of this segment.
The next step is the give each segment an idx to mark their position. The purple letters on top of the segments are the idxs.
It's not beautiful to put big segments in the bottom, so we can reverse it like this: 
We always use $$$ls$$$ to represent the left son of a segment and use $$$rs$$$ to represent its right son. We can find that $$$ls = pos \times 2$$$ and $$$rs = ls + 1$$$ ($$$pos$$$ is the id of the father segment). So we have:
#define ls (o << 1)
#define rs (ls | 1)
Note that there are some segments which have many idxs. This operation can help us to find the $$$ls$$$ and $$$rs$$$ quickly, but it will waste some memery. Scientists calculation shows that the total memery we use will not exceed four times the length of the interval.
code of build tree:
void build(int o, int l, int r)
{
if (l == r)
{
sum[o] = a[l];
return;
}
int mid = (l + r) >> 1;
//get the middle and cut the segment into two
build(ls, l, mid);
build(rs, mid + 1, r);
//build the left son and the right son
sum[o] = sum[ls] + sum[rs];
}

Let look at the example. If I want to query the sum from $$$a_3$$$ to $$$a_9$$$, we don't have to add them up, we can add sum[l = 3, r = 4], sum[l = 5, r = 8] and sum[l = 9, r = 9]. The time complexity is only $$$O(\log(n))$$$.
Prove: we will add only a number in a layer, and there are at most $$$\log(n)$$$ layers, so the number of the operation will not exceed $$$O(\log(n))$$$.
That read the code together:
ll query(int o, int l, int r)
{
if (ql <= l && r <= qr) return sum[o];
int mid = (l + r) >> 1;
ll s = 0;
push_down(o, l, r);
//push_down is used to update, I will explain it next.
if (ql <= mid) s += query(ls, l, mid);
if (mid < qr) s += query(rs, mid + 1, r);
return s;
}
In the code, I use $$$ql$$$ to represent the left endpoint of the query, and use $$$qr$$$ to represent the right endpoint.
if (ql <= l && r <= qr) return sum[o]; This means if our query contains the segment, add it up.
if (ql <= mid) s += query(ls, l, mid);
if (mid < qr) s += query(rs, mid + 1, r);
If a part of the query is in the left son, visit it. If a part of the query is in the right son, visit it.
"Lazy Tag" is the most important part in updation. This method can reduce the time complexity to $$$O(\log(n))$$$ for each updation. It's obvious that we can't update the whole tree, or the time complexity will be $$$O(n)$$$ like build tree. To reduce the time complexity, if a segment is not queried now, we don't have to update it at present. We usually give it a tag to record how we update it. For example, if we want to update an array and query the sum of an interval, for each "add" operation, we do not add numbers to each segment, we only have to give a "add tag" to the some segments.

For example, if we want to add $$$2$$$ from $$$2$$$ to $$$5$$$. We should give segment number $$$9$$$, $$$17$$$ and $$$20$$$ an "add tag" to sign them.
Note that segment we signed are all a part of the interval we operate on.
This picture shows what the tree is like after the operation.
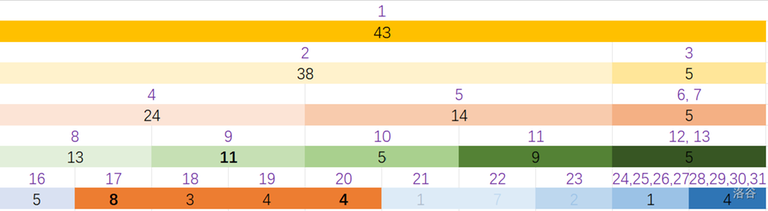
void change(int o, int l, int r)
{
if (ql <= l && r <= qr)
{
apply_add_tag(o, l, r, qv);
return;
}
push_down(o, l, r);
int mid = (l + r) >> 1;
if (ql <= mid) change(ls, l, mid);
if (mid < qr) change(rs, mid + 1, r);
// just like what we do in query
sum[o] = sum[ls] + sum[rs];
// push up the sum of the segment
}
if (ql <= l && r <= qr)
{
apply_add_tag(o, l, r, qv);
return;
}
This means if the segment is contain in the interval, we don't have to visit its sons because when we query we can push up this segment directly without ask the sons. This is the reson why we can operate on it and return.
void apply_add_tag(int o, int l, int r, ll v)
{
sum[o] += (ll)(r - l + 1) * v;
add[o] += v;
}
sum[o] += (ll)(r - l + 1) * v; This means the real value the segment should add = the value each node add * the length of the segment.
When we query the segment which has a tag. We should update it. (of course we don't have to use extra time, we can update this when we query / update a new interval.
void push_down(int o, int l, int r)
{
if (add[o] != 0)
{
int mid = (l + r) >> 1;
apply_add_tag(ls, l, mid, add[o]);
apply_add_tag(rs, mid + 1, r, add[o]);
add[o] = 0;
}
}
add[o] = 0; Node that we have to clear the tag on the father segment after we push the tag down.
Someone may ask " when we clear the tag, how can we know know the real value of the segment?"
Don't forget that there is a push up operation when we update sum[o] = sum[ls] + sum[rs]; and there is a push down operation when we query.
There is a kind of problems which want you to calculate the distant of the shortest path from some verdicts to other verdicts. This kind of problems are called "shortest path" in graph.
For example, in this graph, the distant of shortest path from verdict $$$1$$$ to verdict $$$6$$$ is $$$6$$$. And the distant of the shortest path from verdict $$$1$$$ to verdict $$$4$$$ is $$$5$$$.
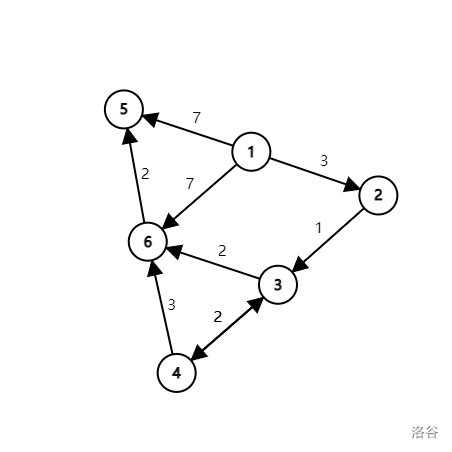
Specifically, there are $$$2$$$ of subproblems in shortest path:
Single sourse (one start point)
Multi source (multi start point)
In shortest path with single sourse, we should calculate the distant of the shortest path from one verdict (Lets suppose the sourse is verduct $$$1$$$) to others. Dijkstra is the most common algorithm to solve this sort of problems.
Node that Dijkstra can only solve the problems with nonnegtive edge weight. For graphs with negtive edge weight, you can only use Bellman Ford.
Dijkstra is a kind of greedy. In each turn, We select the verdict with the shortest distance from the sourse and get the shortest path to it. After that we update the distant from the sourse to other verdict.
Lets look at the example:

| node | distant to the sourse(now) | shortest path |
|---|---|---|
| $$$1$$$ | \ | $$$0$$$ |
| $$$2$$$ | $$$3$$$ | \ |
| $$$3$$$ | \ | \ |
| $$$4$$$ | \ | \ |
| $$$5$$$ | $$$7$$$ | \ |
| $$$6$$$ | $$$7$$$ | \ |
Get the distant of the shortest path to verdict $$$2$$$.
| node | distant to the sourse(now) | shortest path |
|---|---|---|
| $$$1$$$ | \ | $$$0$$$ |
| $$$2$$$ | \ | $$$3$$$ |
| $$$3$$$ | $$$1+3=4$$$ | \ |
| $$$4$$$ | \ | \ |
| $$$5$$$ | $$$7$$$ | \ |
| $$$6$$$ | $$$7$$$ | \ |
Get the distant of the shortest path to verdict $$$3$$$.
| node | distant to the sourse(now) | shortest path |
|---|---|---|
| $$$1$$$ | \ | $$$0$$$ |
| $$$2$$$ | \ | $$$3$$$ |
| $$$3$$$ | \ | $$$4$$$ |
| $$$4$$$ | $$$6$$$ | \ |
| $$$5$$$ | $$$7$$$ | \ |
| $$$6$$$ | $$$6$$$ | \ |
Get the distant of the shortest path to verdict $$$4$$$ and verdict $$$6$$$.
| node | distant to the sourse(now) | shortest path |
|---|---|---|
| $$$1$$$ | \ | $$$0$$$ |
| $$$2$$$ | \ | $$$3$$$ |
| $$$3$$$ | \ | $$$4$$$ |
| $$$4$$$ | \ | $$$6$$$ |
| $$$5$$$ | $$$7$$$ | \ |
| $$$6$$$ | \ | $$$6$$$ |
Get the distant of the shortest path to verdict $$$4$$$ and verdict $$$6$$$.
| node | distant to the sourse(now) | shortest path |
|---|---|---|
| $$$1$$$ | \ | $$$0$$$ |
| $$$2$$$ | \ | $$$3$$$ |
| $$$3$$$ | \ | $$$4$$$ |
| $$$4$$$ | \ | $$$6$$$ |
| $$$5$$$ | \ | $$$7$$$ |
| $$$6$$$ | \ | $$$6$$$ |
Get the distant of the shortest path to verdict $$$7$$$.
The way Dijkstra is just like Prim (an algorithm of MST), we find the nearest verdict and them update the distant to other verdict.
Code: Dijkstra without heap, time complexity $$$O(n^2)$$$:
void dijkstra()
{
int node;
for (int i = 1; i <= n; ++i)
{
node = -1;
for (int j = 1; j <= n; ++j)
{
if (!vis[j] && (node == -1 || dis[j] < dis[node]))
node = j;
}
vis[node] = 1;
for (int j = 1; j <= n; ++j)
dis[j] = min(dis[j], dis[node] + g[node][j]);
}
}
Code Dijkstra with heap, time complexity $$$O(m\log(n))$$$:
void dijkstra()
{
dis[s] = 0;
Q.push((node){0, s});
while (!Q.empty())
{
node now = Q.top();
Q.pop();
int npos = now.pos, ndis = now.dis;
if (vis[npos] == false)
{
vis[npos] = true;
for (re int i = head[npos]; i != 0; i = e[i].next)
{
int to_pos = e[i].to;
if (dis[to_pos] > dis[npos] + e[i].dis)
{
dis[to_pos] = dis[npos] + e[i].dis;
if (vis[to_pos] == false)
Q.push((node){dis[to_pos], to_pos});
}
}
}
}
}
Connected component is a very important part of graphs. I wrote $$$3$$$ ariticals about it recently, they are:
After you read this articals, You will have a deeper understanding of the algorithm of Tarjan.
The algorithm of Tarjan is used to solve some problems which is about the connectedness of the Graph. Today I am going to introduce the key to solving E-DCC by Tarjan.
This problem is the template of V-DCC.
The full name of E-DCC is vertex double connectivity component.
An E-DCC is a component that you cut any one of the vertexs, the graph is still connected.
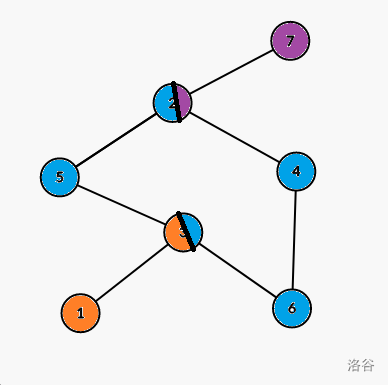
For example, in this graph, nodes in same color are in the same V-DCC, and there are $$$3$$$ V-DCCs in this graph. They are:
node 1, 3
node 2, 3, 4, 5, 6
node 2, 7
First, we should know what "cut vertex" is. A "cut vertex" is a vertex in the graph, and if you cut the vertex off, the graph is not connected.
Tarjan is one of the algorithms which can solve this problems.
First I am going to introduce two arrays to you:
$$$low_x$$$: An array of trace values representing the minimum idx of points on a search tree rooted at x which can be reached by only one edge which is not in the search tree.
$$$dfn_x$$$: Timestamp array, representing the order it was visited.
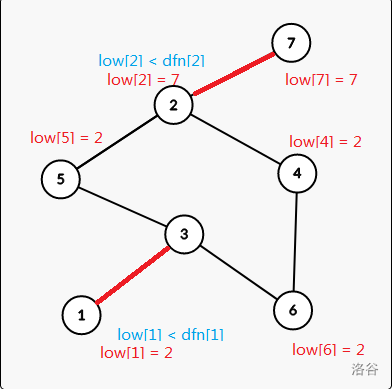
For example we can get the two values of the nodes:
We assume that there is an undirected edge from the node $$$x$$$ to the node $$$y$$$. There are two conditions:
low[x] = min(low[x], low[y]);low[x] = min(low[x], dfn[y]);Node that: In the secound condition, it is $$$dfn_y$$$, and it isn't $$$low_y$$$.
We should look back to the defination:
by only one edge which is not in the search tree
Only one edge!
If a vertex $$$x$$$ is a cut vertex, if and only if $$$dfn_x \le low_y$$$.**
Note that this is not as same as "Bridge".
Lets look back to the example:

For node $$$2$$$, $$$low_2 = 7$$$ and $$$dfn_2 \le low_2$$$, so it is a cut vertex, because if node $$$2$$$ is cut, there isn't a path to connect node $$$7$$$.
Code of finding "cut vertex":
// note that "root" means "father"
void tarjan(int node, int root)
{
int scnt = 0;
dfn[node] = low[node] = ++num;
for (int i = head[node]; i; i = e[i].next)
{
const int to = e[i].to;
if (dfn[to] == 0)
{
++scnt;
fa[to] = node;
tarjan(to, root);
low[node] = min(low[node], low[to]);
if (low[to] >= dfn[node] && node != root) cut[node] = 1;
}
else if (to != fa[node])
low[node] = min(low[node], dfn[to]);
}
if (scnt >= 2 && node == root)
cut[root] = 1;
}
We can find that some vertexs are in more than one V-DCC. They are "cut vertex".
In any V-DCC, there are vertexs on the "border" of it, but not in the center. This is because if a cut vertex is in the center, we cut it, the connected component will break into two, but a cut vertex on the border of the V-DCC can be allowed, because when the vertex is cut, one of the new connected component is "empty", and the V-DCC will not break into two.
Because of this, we can set up a stack. When we visit a new vertex, we put it into the stack. When we find a "cut vertex", we should pop the elements in the stack until the cut vertex become the top of the stack. We shouldn't pop the "cut vertex", because the cut vertex is in more that one V-DCC.
Code of V-DCC:
void tarjan(int node)
{
dfn[node] = low[node] = ++id;
st[++top] = node;
if (node == root && head[node] == 0)
{
dcc[++sum].push_back(node);
return;
}
for (int i = head[node]; i; i = e[i].nxt)
{
int to = e[i].to;
if (dfn[to] == 0)
{
tarjan(to);
low[node] = min(low[node], low[to]);
if (low[to] >= dfn[node])
{
++sum;
int tmp;
while (1)
{
tmp = st[top--];
dcc[sum].push_back(tmp);
if (tmp == to) break;
}
dcc[sum].push_back(node);
}
}
else low[node] = min(low[node], dfn[to]);
}
}
You can read this aritical to learn some basic operations of segment tree.
"Lazy Tag" is the most important part in updation. This method can reduce the time complexity to $$$O(\log(n))$$$ for each updation. It's obvious that we can't update the whole tree, or the time complexity will be $$$O(n)$$$ like build tree. To reduce the time complexity, if a segment is not queried now, we don't have to update it at present. We usually give it a tag to record how we update it. For example, if we want to update an array and query the sum of an interval, for each "add" operation, we do not add numbers to each segment, we only have to give a "add tag" to the some segments.

For example, if we want to add $$$2$$$ from $$$2$$$ to $$$5$$$. We should give segment number $$$9$$$, $$$17$$$ and $$$20$$$ an "add tag" to sign them.
Note that segment we signed are all a part of the interval we operate on.
This picture shows what the tree is like after the operation.

void change(int o, int l, int r)
{
if (ql <= l && r <= qr)
{
apply_add_tag(o, l, r, qv);
return;
}
push_down(o, l, r);
int mid = (l + r) >> 1;
if (ql <= mid) change(ls, l, mid);
if (mid < qr) change(rs, mid + 1, r);
// just like what we do in query
sum[o] = sum[ls] + sum[rs];
// push up the sum of the segment
}
if (ql <= l && r <= qr)
{
apply_add_tag(o, l, r, qv);
return;
}
This means if the segment is contain in the interval, we don't have to visit its sons because when we query we can push up this segment directly without ask the sons. This is the reson why we can operate on it and return.
void apply_add_tag(int o, int l, int r, ll v)
{
sum[o] += (ll)(r - l + 1) * v;
add[o] += v;
}
sum[o] += (ll)(r - l + 1) * v; This means the real value the segment should add = the value each node add * the length of the segment.
When we query the segment which has a tag. We should update it. (of course we don't have to use extra time, we can update this when we query / update a new interval.
void push_down(int o, int l, int r)
{
if (add[o] != 0)
{
int mid = (l + r) >> 1;
apply_add_tag(ls, l, mid, add[o]);
apply_add_tag(rs, mid + 1, r, add[o]);
add[o] = 0;
}
}
add[o] = 0; Node that we have to clear the tag on the father segment after we push the tag down.
Someone may ask " when we clear the tag, how can we know know the real value of the segment?"
Don't forget that there is a push up operation when we update sum[o] = sum[ls] + sum[rs]; and there is a push down operation when we query.
Segment Tree is a useful data structure that can solve problems like RMQ in $$$O(n)$$$ build tree and $$$O(\log(n))$$$ for each query or update.
What can it query?
sum
maxinum / minium
gcd / lcm
other thing that can be push up
Lets use segment Tree to query the sum of an array.

Lets look at the example, the tree is just like many segments!
It's easy to find that the number on the bottom is the sum of the two numbers on it.
The $$$l$$$ and $$$r$$$ note the left endpoint and the right endpoint of this segment.
The next step is the give each segment an idx to mark their position. The purple letters on top of the segments are the idxs.
It's not beautiful to put big segments in the bottom, so we can reverse it like this: 
We always use $$$ls$$$ to represent the left son of a segment and use $$$rs$$$ to represent its right son. We can find that $$$ls = pos \times 2$$$ and $$$rs = ls + 1$$$ ($$$pos$$$ is the id of the father segment). So we have:
#define ls (o << 1)
#define rs (ls | 1)
Note that there are some segments which have many idxs. This operation can help us to find the $$$ls$$$ and $$$rs$$$ quickly, but it will waste some memery. Scientists calculation shows that the total memery we use will not exceed four times the length of the interval.
code of build tree:
void build(int o, int l, int r)
{
if (l == r)
{
sum[o] = a[l];
return;
}
int mid = (l + r) >> 1;
//get the middle and cut the segment into two
build(ls, l, mid);
build(rs, mid + 1, r);
//build the left son and the right son
sum[o] = sum[ls] + sum[rs];
}

Let look at the example. If I want to query the sum from $$$a_3$$$ to $$$a_9$$$, we don't have to add them up, we can add sum[l = 3, r = 4], sum[l = 5, r = 8] and sum[l = 9, r = 9]. The time complexity is only $$$O(\log(n))$$$.
Prove: we will add only a number in a layer, and there are at most $$$\log(n)$$$ layers, so the number of the operation will not exceed $$$O(\log(n))$$$.
That read the code together:
ll query(int o, int l, int r)
{
if (ql <= l && r <= qr) return sum[o];
int mid = (l + r) >> 1;
ll s = 0;
push_down(o, l, r);
//push_down is used to update, I will explain it next.
if (ql <= mid) s += query(ls, l, mid);
if (mid < qr) s += query(rs, mid + 1, r);
return s;
}
In the code, I use $$$ql$$$ to represent the left endpoint of the query, and use $$$qr$$$ to represent the right endpoint.
if (ql <= l && r <= qr) return sum[o]; This means if our query contains the segment, add it up.
if (ql <= mid) s += query(ls, l, mid);
if (mid < qr) s += query(rs, mid + 1, r);
If a part of the query is in the left son, visit it. If a part of the query is in the right son, visit it.
I will introduce it in my next aritical.
"SCC" means "strongly connected components.
In a directed graph , the nodes in the same SCC can visit each other.
In an easy way of understanding, if node $$$x$$$ and node $$$y$$$ are in the same SCC, there is a path from $$$x$$$ to $$$y$$$ and a path from $$$y$$$ to $$$x$$$.
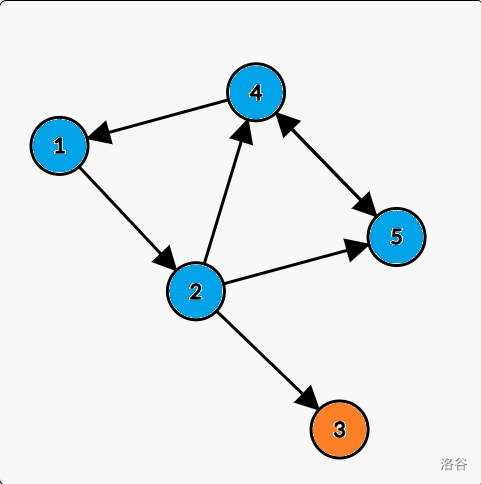
For example, in this graph, nodes in same color are in the same SCC:
This problem is the templet of SCC. After you read this aritical, you can go and solve it.
Tarjan is one of the algorithms which can solve this problems.
First I am going to introduce two arrays to you:
$$$low_x$$$: An array of trace values representing the minimum idx of points on a search tree rooted at $$$x$$$ which can be reached by only one edge which is not in the search tree.
$$$dfn_x$$$: Timestamp array, representing the order it was visited.
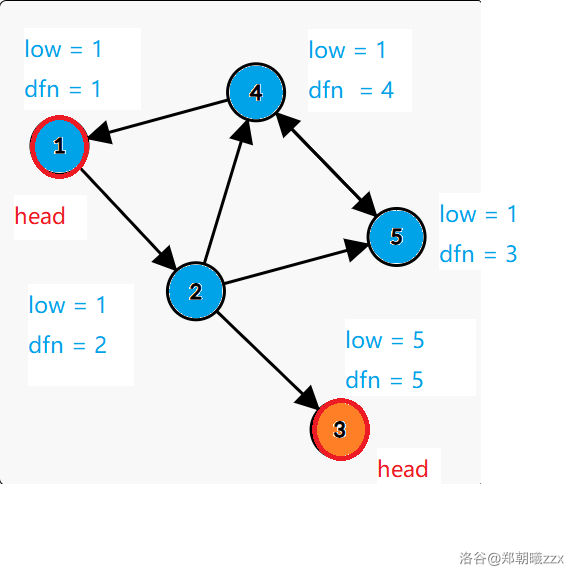
For example we can get the two values of the nodes:
We assume that there is an undirected edge from the node $$$x$$$ to the node $$$y$$$. There are two conditions:
low[x] = min(low[x], low[y]);low[x] = min(low[x], dfn[y]);Node that: In the secound condition, it is $$$dfn_y$$$, and it isn't $$$low_y$$$.
We should look back to the defination:
by only one edge which is not in the search tree
Only one edge!
Lets look back to the sample:

We can find that in each SCC there is a "head" which $$$low_x = dfn_x$$$. In this graph, the "heads" are node $$$1$$$ and node $$$3$$$.
We can use a stack to put the nodes we visited. When we get a "head", we should pop the elements in the stack and put them in the same SCC.
Lets read the sample together:
| node we visit | nodes in the stack | "head" | SCC |
|---|---|---|---|
| $$$1$$$ | $$$1$$$ | ||
| $$$2$$$ | $$$1\ 2$$$ | ||
| $$$5$$$ | $$$1 \ 2 \ 5$$$ | ||
| $$$4$$$ | $$$1 \ 2 \ 5 \ 4$$$ | There is an edge from $$$4$$$ to $$$1$$$, and we find a "head" node $$$1$$$ | |
| pop the stack | $$$empty$$$ | $$$1 \ 2 \ 5 \ 4$$$ | |
| $$$3$$$ | $$$3$$$ | $$$low_3 = dfn_3 = 5$$$, so node $$$3$$$ is a "head" | |
| pop the stack | $$$empty$$$ | $$$1 \ 2 \ 5 \ 4 \ and \ 3$$$ |
In this way, we can find the SCCs.
code in c++
void tarjan(int node)
{
printf("%d ", node);
stack[top++] = node;
low[node] = dfn[node] = ++id;
for (int i = head[node]; i; i = e[i].nxt)
{
int to = e[i].to;
if (dfn[to] == 0)
{
tarjan(to);
low[node] = min(low[node], low[to]);
}
else if (scc[to] == 0)
low[node] = min(low[node], dfn[to]);
}
if (low[node] == dfn[node])
{
++color_cnt;
ans.push_back(vector <int>());
while (true)
{
int to = stack[--top];
ans[color_cnt-1].push_back(to);
scc[to] = color_cnt;
if (node == to) break;
}
}
}
If you want to learn more about connected components, can can read this aritical : A brief introduction of Tarjan and E-DCC(EBC).
The algorithm of Tarjan is used to solve some problems which is about the connectedness of the Graph. Today I am going to introduce the key to solving E-DCC by Tarjan.
This problem is the template of E-DCC.
The full name of E-DCC is edge double connectivity component.
Some people call it EBC (Edge Biconnected Component).
An E-DCC is a component that you cut any one of the edges, the graph is still connected.
For example, in this graph, nodes in same color are in the same E-DCC, and there are $$$3$$$ E-DCCs in this graph. They are:
node $$$1$$$
node $$$2$$$, $$$3$$$, $$$4$$$, $$$5$$$, $$$6$$$
node $$$7$$$
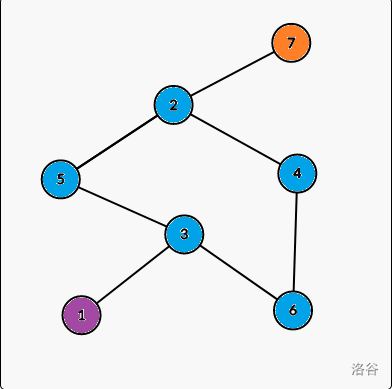
First, we should know what BRIDGE is. - A bridge is an edge in the graph, and if you cut the edge off, the graph is not connected.
Tarjan is one of the algorithms which can solve this problems.
First I am going to introduce two arrays to you:
$$$low_x$$$: An array of trace values representing the minimum idx of points on a search tree rooted at $$$x$$$ which can be reached by only one edge which is not in the search tree.
$$$dfn_x$$$: Timestamp array, representing the order it was visited.
For example we can get the two values of the nodes:

We assume that there is an undirected edge from the node $$$x$$$ to the node $$$y$$$. There are two conditions:
low[x] = min(low[x], low[y]);low[x] = min(low[x], dfn[y]);Node that: In the secound condition, it is $$$dfn_y$$$, and it isn't $$$low_y$$$.
We should look back to the defination:
by only one edge which is not in the search tree
Only one edge!
If the undirected edge from x to y is a Bridge, if and only if (necessary and sufficient conditions) $$$dfn_x \lt low_y$$$.
Lets look back to the example:

For node $$$2$$$, $$$dfn_2 = 2$$$ and $$$low_2 = 7$$$, so edge (2 -> 7) is a bridge.
Because if the edge was cut, we can not goes back to node $$$7$$$ from node 2.
// code of finding bridges
void tarjan(int node, int in_edge)
{
dfn[node] = low[node] = ++id;
for (int i = head[node]; i; i = e[i].nxt)
{
const int to = e[i].to;
if (dfn[to] == 0)
{
tarjan(to, i);
if (dfn[node] < low[to])
b[i] = b[i ^ 1] = 1;
low[node] = min(low[node], low[to]);
}
else if (i != (in_edge ^ 1))
low[node] = min(low[node], dfn[to]);
}
}
If you know how to find Bridges, it will be easy for you to find all the E-DCC.
Cut all the bridges off, then we can get all the E-DCC.
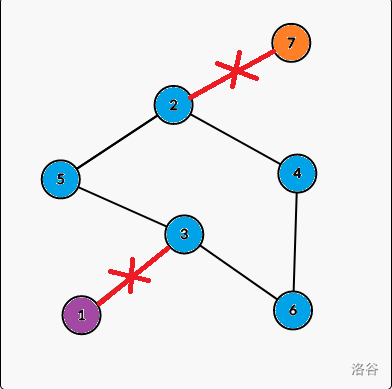
We can solve the problem like this because in each E-DCC there is no bridges.
// code of finding E-DCC
void dfs(int node, int ndcc)
{
dcc[node] = ndcc;
Ans[ndcc - 1].push_back(node);
for (int i = head[node]; i; i = e[i].nxt)
{
int to = e[i].to;
if (dcc[to] || b[i]) continue;
dfs(to, ndcc);
}
}
| Name |
|---|


