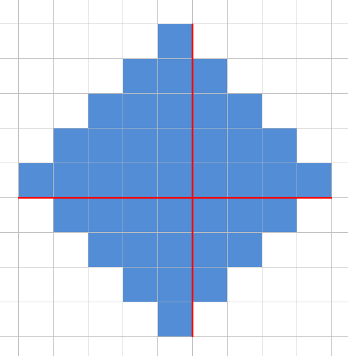
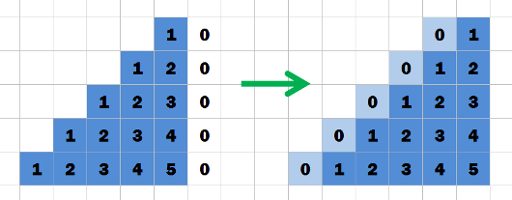
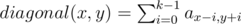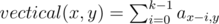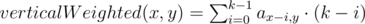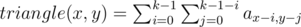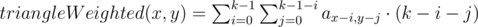Количество различных строк длины 2: 262 = 676, а суммарная длина всех строк не превосходит 600. Это значит, что длина ответа не превосходит 2. Поэтому можно просто проверить все строки длины 1 и 2.
Построим двудольный граф с n вершинами (для сотрудников) в одной доле, и m вершинами (для языков) в другой. Если сотрудник знает язык, значит должно быть ребро между соответствующими вершинами. Теперь задача выглядит понятнее: нужно добавить в граф минимальное количество ребер, чтобы появилась компонента связности, содержащая всех n сотрудников. Очевидно, что это число равно количеству компонент связности, включающих хотя бы одного сотрудника, минус 1. Но есть одно исключение (претест #4): если изначально вообще никто не знает ни один язык, то ответ равен n, так как мы не можем добавлять ребра напрямую между людьми.
Для m = 3, n = 5 и m = 3, n = 6 решения не существует.
Научимся строить ответ для n = 2m, где m ≥ 5 и нечетное. Расставим m точек на окружности достаточно большого радиуса — это будет внутренний многоугольник. Чтобы получить внешний многоугольник, умножим все координаты внутреннего на 2. Более точно (1 ≤ i ≤ m):
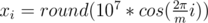
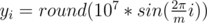
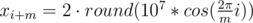
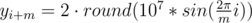
Если m четное, построим решение для m + 1 и удалим по одной точке из каждого многоугольника. Если n < 2m, удалим 2m - n точек из внутреннего многоугольника.
К сожалению, такое решение не работает для m = 4, n = 7 и m = 4, n = 8.
Альтернативное решение — поставить m точек на выпуклой функции (например, y = x2 + 107), и n - m точек на вогнутой функции (например, y = - x2 - 107). Так решал rng_58 — 3210150.
Заметим, что горизонтальные и вертикальные разрезы независимы. Рассмотрим любую горизонтальную линию: она содержит m единичных отрезков, и в любой ситуации всегда возможно уменьшить длину неразрезанной части так, как этого хочет игрок. Представим, что игрок наращивает отрезок от края поля, увеличивая его длину на 1 за раз. Каждый раз суммарная длина неразрезанной части уменьшается либо на 0, либо на 1. В конце, понятно, достигает 0.
То же самое верно и для вертикальных линий. Значит, если бы не было начальных разрезов, игра превратилась бы в ним с n - 1 кучками по m камней и m - 1 кучками по n камней. Решается простой формулой.
Начальные k разрезов добавляют только техническую сложность. Для каждой вертикальной/горизонтальной линии, содержащей хотя бы один разрез, размер соответствующей кучки нужно уменьшить на суммарную длину всех разрезов на этой линии.
Как делать первый ход в ниме: пусть res — результат игры, а ai — размер i-ой кучки. Тогда результат игры без i-ой кучки — 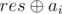 . Мы хотим заменить ai на какое-то x, чтобы
. Мы хотим заменить ai на какое-то x, чтобы 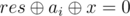 . Понятно, что единственное подходящее значение
. Понятно, что единственное подходящее значение 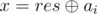 . Итоговое решение: находим такую кучку, что
. Итоговое решение: находим такую кучку, что 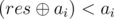 , и уменьшаем ai до
, и уменьшаем ai до 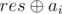 .
.
Пусть зафиксирован набор подзадач, которые мы будем решать. Давайте определим, в каком порядке их нужно решать. Понятно, что легкие подзадачи (и сложные подзадачи с probFail = 0) в любом случае не упадут. То есть наше штрафное время не меньше времени отправки последней такой <<надежной>> подзадачи. Значит, в первую очередь нужно решить все такие подзадачи. Подзадачи с probFail = 1 вообще не имеет смысла решать. Рассмотрим подзадачи с 0 < probFail < 1. Пусть есть две подзадачи i и j, которые мы решаем подряд. Посмотрим, в каком случае выгодно их решать в порядке i, j, а не наоборот. Мы не учитываем остальные задачи, так как они ни на что не влияют.
(timeLargei + timeLargej)(1 - probFailj) + timeLargei(1 - probFaili)probFailj < (timeLargei + timeLargej)(1 - probFaili) + timeLargej(1 - probFailj)probFaili
- probFailj·timeLargej - timeLargei·probFailj·probFaili < - probFaili·timeLargei - timeLargej·probFaili·probFailj
timeLargei·probFaili(1 - probFailj) < timeLargej·probFailj(1 - probFaili)
timeLargei·probFaili / (1 - probFaili) < timeLargej·probFailj / (1 - probFailj)
Получается, что если отсортировать подзадачи по данному компаратору, будет оптимальный порядок решения. Заметим, что подзадачи probFail = 0, 1 тоже отсортируются правильно, то есть не являются частными случаями.
Вернемся к исходной задаче. Первым делом отсортируем все задачи полученным компаратором — ясно, что в другом порядке решать никогда не выгодно по времени, а количество очков от порядка не зависит. Посчитаем такую динамику: z[i][j] = пара из максимального матожидания суммы очков и минимального штрафного времени при данной сумме очков, если мы рассмотрели первые i задач, и прошло j реальных минут контеста. Возможно 3 перехода:
либо мы не трогаем i-ую задачу: переходим в z[i + 1][j] с такими же матожиданиями
либо мы решаем только легкую подзадачу: переходим в z[i + 1][j + timeSmalli], при этом очки увеличиваются на scoreSmalli, и штрафное время — на timeSmalli (мы как бы считаем, что будем решать i-ую задачу в самом начале контеста)
либо мы решаем обе подзадачи: переходим в z[i + 1][j + timeSmalli + timeLargei], при этом очки увеличиваются на scoreSmalli + (1 - probFaili)scoreLargei, и штрафное время становится равным timeSmalli + (1 - probFaili)(j + timeLargei) + probFaili·penaltyTime(z[i][j]), где penaltyTime(z[i][j]) — значение матожидания штрафного времени из динамики
Итоговый ответ — наилучшее из значений z[n][i], (0 ≤ i ≤ t).
Матожидание очков может быть числом порядка 1012 с 6 знаками после точки, то есть его нельзя хранить в типе double абсолютно точно, а любая погрешность в вычислении матожидания очков может привести к ошибке в матожидании времени (претест #7). Чтобы этого избежать, можно, например, домножить все вероятности на 106, и считать первое матожидание в целых числах.
277E - Бинарное дерево на плоскости
Если бы не было ограничения на "бинарность", задача бы решалась простой жадностью. Каждая вершина дерева (за исключением корня) должна иметь ровно одного предка. При этом каждая вершина может быть родителем для любого количества вершин.
Назначим каждой вершине i (исключая корень) в качестве предка такую вершину pi, что ypi > yi и при этом pi — ближайшая к i. Перенумеруем все вершина в порядке невозрастания y. Очевидно, что pi < i (2 ≤ i ≤ n). То есть мы таким образом задали корневое дерево, в котором все дуги идут вниз, и оно минимально по длине.
Теперь вспомним про "бинарность". Но она на самом деле мало чего меняет: жадность превращается в min-cost-max-flow на той же матрице расстояний, но только теперь в каждую вершину должно приходить не более 2 единиц потока.