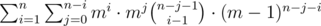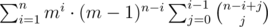Hello everyone! I would like to invite you to participate in HackerEarth HourStorm #2. It’s the second version of a short contest, that runs for 1 hour! The problem set consists of 3 traditional algorithmic tasks of various difficulties. The contest starts on the 11th of August i.e today at 9.30- PM IST
For traditional algorithmic tasks, you will receive points for every test case your solution passes — so you can get some points with partial solutions as well. Check contest page for more details about in-contest schedule and rules.
send_nodes and I have worked on the preparation of the contest. As usual, there will be some prizes for the top three competitors:
$75 Amazon gift card $50 Amazon gift card $25 Amazon gift card
In addition, top 5 on the scoreboard with rating less than 1600 will win HackerEarth t-shirts. The problems are on the easier side, giving everybody a fair shot at taking home the prizes. Good luck to everyone, and let's discuss the problems after the contest!
Note that the contest begins after the end of the CF Round.
Update : The contest begins in 15 minutes









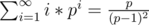 , as
, as 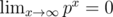
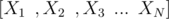 , where , there are cyclic dependencies among the variables for their expected values, i.e consider
, where , there are cyclic dependencies among the variables for their expected values, i.e consider 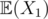 depends on
depends on 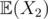 ,
, 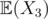 and
and 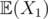 . So, there exists an infinite loop for calculating the Expected values of the random variables.
. So, there exists an infinite loop for calculating the Expected values of the random variables. 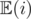 denote the expected number of steps needed to reach node
denote the expected number of steps needed to reach node 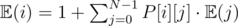 .
. 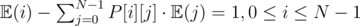 . So the system is :
. So the system is :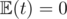 . So, the part
. So, the part 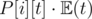 does not affect any of the equations. So, just remove the
does not affect any of the equations. So, just remove the 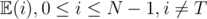
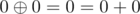 mod
mod 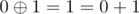 mod
mod 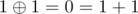 mod
mod  . For example ,
. For example , 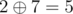 i.e. ,
i.e. , 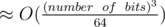 .
.