Привет всем!

556A - Дело о нулях и единицах

Если в последовательности остались хотя бы одни единица и ноль, тогда существует подстрока 01 или 10, которую можно удалить. При этом порядок удаления не важен: в любом случае мы сделаем min(#единиц, #нулей) операций, так как за раз удаляется один ноль и одна единица. Поэтому ответ: #единиц + #нулей - 2min(#единиц, #нулей) = |#единиц - #нулей|.

Время: O(n).

556B - Дело о поддельных шестеренках

Заметим, что через n нажатий кнопки система приходит в исходное положение. Поэтому самое простое решение — это промоделировать процесс из n шагов и, если на одном из них встретится последовательность 0, 1, ... , n - 1, выдать "Yes", иначе "No". Но можно это решение ускорить. Например, сразу по значению первого элемента определить нужное количество нажатий, перейти в это положение и один раз проверить.

Время: O(n) или O(n²); решения: O(n) и O(n^2)

555A - Дело о матрешках

Предположим нам не нужно разбирать некоторую последовательность. Тогда ни в одну из матрешек этой последовательности не нужно вставить другую. Поэтому нам не нужно разбирать последовательность матрешек лишь в случае, если они идут подряд, начиная с 1. Пусть длина этой последовательности равна l. Тогда вытащить одну из другой нам нужно будет n - k - l + 1 раз, при этом останется одна цепочка из l матрешек 1 → 2 → ... → l и остальные цепочки по одной матрешке. Всего n - k + 1 цепочка, поэтому вложить одну в другую нужно n - k раз. Всего будет сделано 2n - l - 2k + 1 операций.

Время: O(n); решение.

555B - Дело о беглеце

Между островами i и i + 1 мы можем положить мост, длина которого попадает в отрезок [l_i + 1 - r_i;r_i + 1 - l_i]. Получаем задачу: есть n - 1 отрезков и m точек на прямой, необходимо каждому отрезку сопоставить какую-то точку, лежащую в нем, причем каждую точку можно сопоставить только одному отрезку. Будем идти по точкам слева направо, и хранить в сете отрезки, которые еще ничему не сопоставлены и которые содержат рассматриваемую точку. Пусть мы обрабатываем очередную точку. Сначала добавим в сет все отрезки, которые начинаются в этой точке. Далее выберем из них тот, чей правый конец имеет наименьшую координату. Утверждается, что этот алгоритм находит ответ, если он есть. Предположим это не так. Пусть мы на каком-то шаге выбрали для точки A другой отрезок (пропускать точку не имеет смысла). Тогда посмотрим, какая точка B сопоставлена отрезку, который был бы выбран нашим решением. Точка B лежит заведомо правее A. Поэтому мы можем поменять точки для этих отрезков и снова получить ответ.

Время: O((n + m)log(n + m)); решение.

555C - Дело о шоколаде

Решим задачу с помощью двух деревьев отрезков: для столбцов и для строк. Будем хранить для каждого столбца самую нижнюю съеденную дольку, а для каждой строки — самую левую. Пусть приходит запрос x y L. Находим значение в дереве отрезков для строк на месте y. Пусть это значение равно ans. Теперь нужно вывести x - ans и в дереве для столбцов обновить значения на отрезке [ans + 1, x] до y, а в горизонтальном обновить значение в элементе y дo x. Аналогично с запросами типа U. Чтобы разобраться с большими ограничениями на n нужно писать либо неявное дерево отрезков, либо сжатие координат.

Время: O(qlogq) или O(qlogn); решения: 1 and 2.

555D - Дело повышенной секретности

Назовем активной длиной L_a длину части веревки от груза до последнего встреченного колышка. После каждого встреченного колышка активная длина уменьшается. Будем моделировать процесс для каждой длины веревки независимо. На каждом шаге будем бинарным поиском находить, за какой колышек зацепится груз сейчас. При этом если активная длина при этом уменьшается хотя бы вдвое или мы делаем первый шаг, то просто переходим к следующему шагу. А иначе пусть текущий колышек имеет номер i, следующий — j (без ограничения общности i < j). Тогда заметим, что после колышка j мы снова зацепимся именно за колышек i. Действительно, 2(x_j - x_i) ≤ L_a, поэтому веревка зацепится не правее чем за i-й колышек. И либо i = 1, либо L_a ≤ x_i - x_i - 1, поэтому левее, чем за i-й колышек она тоже зацепиться не может. И вообще, пока активная длина будет не меньше, чем x_j - x_i, груз будет наматываться на эту пару колышков, следовательно, можно сделать сразу несколько ходов. При этом после этих ходов длина веревки уменьшится хотя бы вдвое. Поэтому всего таких будет сделано не больше log(L), где L — изначальная длина веревки.

Решение: O(mlogLlogn); решение.

555E - Дело о компьютерной сети

Для начала, сведем задачу к задаче на дереве. В каждой компоненте двусвязности ориентируем ребра в порядке обхода DFS. Утверждается, что мы получим компоненту сильной связности. Пусть это не так. Тогда граф можно разбить на два подграфа A и B так, что не существует ребер, идущих из B в A. Причем изначально ребер между A и B хотя бы два. Но это невозможно, так как, зайдя в эту компоненту B, мы должны будем выйти по одному из ребер между A и B, а это невозможно. Противоречие.

Поэтому мы можем сжать все компоненты двусвязности.

Теперь надо обработать несколько запросов вида “ориентировать ребра на пути” и проследить за отсутствием конфликтов. Подвесим дерево за некоторую вершину и предподсчитаем LCA для исходных пар вершин. Запустим dfs из корня и для каждого поддерева посчитаем количество вершин, являющихся началами исходных путей (переменная а), вершин, являющихся концами исходных путей (переменная b), и предпосчитанных LCA (переменная c). По этой информации можно ориентировать ребро из корня поддерева в предка: если a - c положительно, тогда вверх, если b - c положительно, тогда вниз, если оба положительны, тогда решения нет, если оба нули, то как угодно.

Время: O(n + ql_q) где l_q это время подсчета LCA на запрос; решение, использующее немного другой метод для последней части.

Закончилась четвертая личная интернет-олимпиада.
Здесь предлагается поделиться впечатлениями.

Задачи
Результаты
Тесты и решения жюри (41 мб)
Генераторы тестов и решения жюри

Краткий разбор

А. Муравьи-мутанты
Будем для каждой ловушки слева направо искать муравья, который в нее попадёт. Для первой это будет самый правый муравей, начинающий слева от нее, для второй — самый правый из всех начинающих слева от нее, кроме того одного, который уже словушился, для третьей... Идея понятна, для эффективной реализации достаточно было пройти ловушки постепенно кидая муравьев в стек.

В. Разбиение на камеры
Нельзя, когда n < k, k = 1 или n нечётное, а также если k нечётное и n = k или n = k + 1.
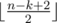Возможное решение: можно на первые две позиции поставить и 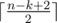а на все остальные — 1.
Поправьте меня, если я неправ.

С. Производство паутины
Несложная динамика. Пусть dp[i] — минимальная стоимость произвести на свет префикс длины i.
Понятно, что перед удалением нет смысла делать добавление символа. Тогда можно ограничиться двумя операциями: добавить символ (стоимость a) и добавить в конец какой-то префикс текущей строки (стоимость b + c·dellen, где dellen — это длина текущей строки минус длина добавляемого префикса).
Тогда dp[1] = a; dp[i] = min(dp[i - 1] + a, min_j(dp[j] + b + c·(j - (i - j)))), где j — все возможные длины префиксов, из которых мы можем получить текущий префикс нашей второй операцией.
Как же теперь определить все нужные j? Для этого стоит заметить что каждый j будет учитываться при пересчете какого-то количества подряд идущих dp[i], причём этот отрезок явно определяется Z-функцией от j. Также нелишним будет учесть, что в формуле пересчета dp[j] + b + c·2·j зависит только от j. а -c·i -- только от i.
Исходя из вышеупомянутого, используем алгоритм заметающей прямой: пусть мы храним множество всех отрезков для всех j, в которых мы сейчас находимся, и для каждого храним первое слагаемое, тогда пересчет очевиден. Поддерживать множество тоже несложно.

D. Эвакуация
Тоже несложная динамика. В этот раз на дереве.
Подвесим дерево. Пусть dp[v] — максимальный момент времени, в который мы можем начать бежать из вершины v вниз по дереву, чтобы спастись, если мы можем это сделать, и -1 иначе. Пересчет: dp[v] = max( - 1, max(min_u(dp[u], t_u) - l_u)), где u — дочерняя вершина, t_u и l_u — параметры ребра .
Решение на 40: ну подвесим дерево за все вершины по очереди и запустим такую штуку.
Решение на 100: применим стандартный приём для подсчета динамики на неподвешенном дереве. Подвесим за произвольную вершину и посчитаем динамику. Затем запустим DFS из корня и для каждой вершины, кроме него, представим, что ребро из нее в предка является как будто является ребром в новую дочернюю вершину, и пересчитаем dp[v] с учетом неё.
Но просто брать для этого пересчета dp[parent] нельзя, так как оно само уже посчитано с учетом (бывшего) dp[v]. Поэтому каждый раз при переходе от parent к v мы передаем параметр up, который показывает, каким бы было dp[parent], если не существовало v. Как найти up? Оно очевидным образом получается из максимального из значении динамики всех дочерних вершин parent, кроме v (а еще и up, который для parent), а чтобы считать его для всех v, надо еще поддерживать два максимальных таких значения.
Для лучшего понимания можно посмотреть мой код.
Судя по всему, решения жюри в архиве основаны на другой идее (сливаемых-переливаемых множеств).

Закончилась третья интернет-олимпиада, которая проходит одновременно и на тех же задачах, что и второй отборочный тур на ИОИП.
Предлагаю здесь поделиться впечатлениями и решениями (а также просьбами запилить ее в тренировки:).

Задачи
Результаты

P.S. Double kill

Здравствуйте.
Как известно, решение задачи должно укладываться в определенные рамки времени работы и используемой памяти. Причем, чаще всего первое критичнее. Но не всегда.
В С++ можно следить за временем работы твоей программы, используя хотя бы clock(). А вот можно ли как-нибудь посмотреть, сколько памяти используется, проверить влезает ли программа в ML? Ну или хотя бы локально поставить такие ограничения?
Спасибо.

Прошла третья интернет-олимпиада, которая проходит одновременно и на тех же задачах, что и второй отборочный тур на ИОИП.
Предлагаю здесь поделиться впечатлениями и решениями (а также просьбами запилить ее в тренировки:).
Результаты ИО
Результаты отбора на ИОИП
Задачи