Lord_F's blog

Codeforces Round #310 Editorial
By Lord_F, history, 9 years ago, In English

Hello, everyone!

556A - Case of the Zeros and Ones

If there still exist at least one 0 and at least one 1 in the string then there obviously exists either substring 01 or substring 10 (or both) and we can remove it. The order in which we remove substrings is unimportant: in any case we will make min(#zeros, #ones) such operations. Thus the answer is #ones + #zeros - 2min(#ones, #zeros) = |#ones - #zeros|.

Time: O(n).

556B - Case of Fake Numbers

Notice that after pressing the button n times gears return to initial state. So the easiest solution is to simulate the process of pressing the button n times and if at some step the active teeth sequence is 0, 1, ... , n - 1 output "Yes" else "No". But this solution can be improved. For instance, knowing the active tooth of the first gear you can quickly determine how many times pressing the button is necessary, go to that state and check the sequence only once.

Time: O(n) or O(n2); solutions: O(n) and O(n^2)

555A - Case of Matryoshkas

Suppose we don't need to disassemble some sequence of dolls. Then no doll can be inserted into no doll from this chain. So we don't need to disassemble a sequence of dolls only if they are consecutive and start from 1. Let the length of this chain be l. Then we will need to get one doll from another n - k - l + 1 times. Now we have a sequence 1 → 2 → ... → l and all other dolls by themselves. n - l + 1 chains in total so we need to put one doll into another n - l times. 2n - k - 2l + 1 operations in total.

Time: O(n); solution.

555B - Case of Fugitive

We can put a bridge between bridges i and i + 1 if its length lies in the segment [li + 1 - ri;ri + 1 - li]. Now we have a well-known problem: there are n - 1 segments and m points on a plane, for every segment we need to assign a point which lies in it to this segment and every point can be assigned only once.

Let's call a segment open if no point is assigned to it. Let's go through all points from left to right and at every moment keep all open segments that contain current point in a BST (std::set). When processing a point it should be assigned to the segment (from our set) that has the leftmost right end.

This algorithm will find the answer if there is one. Suppose this solution is wrong and suppose there is a solution in which point A is assigned to another open segment (there's no sense in skipping this point). Then some point B is assigned to the segment which A was assigned to. B is to the right of A so we can swap them and come to our answer again.

Time: O((n + m)log(n + m)); solution.

555C - Case of Chocolate

Let's solve this problem with two segment trees: we'll keep the lowest eaten piece for each column in one of them and the leftmost eaten piece for each row in another. Suppose we have a query x y L. Position where we'll stop eating chocolate is stored in the row segment tree so we can easily find the number of eaten pieces. After that we need to update both segment trees.

n is rather big in this problem. One way to deal with it is to use coordinate compression. Another is to use implicit segment trees.

Time: O(qlogq) or O(qlogn); solutions: 1 and 2.

555D - Case of a Top Secret

I call the length of the part of the rope from the weight to the last met peg the active length (denoted as La). After each met peg active length is reduced. Let's process queries separately: at each step we can find next peg with using binary search. If active length becomes at least two times shorter or current step is the first one we proceed to the next step. Otherwise say current peg is peg i and the next one is peg j (without loss of generality i < j). Then after peg j the rope will again touch peg i and the weight will again rotate around peg i. Indeed, 2(xj - xi) ≤ La so the weight will rotate around a peg not to the right to peg i. And either i = 1 or La ≤ xi - xi - 1 so it won't also rotate around a peg to the left to peg i. As long as La ≥ xj - xi the weight will rotate around these two pegs so we can skip through several steps momentarily. This way active length is shortened at least twice so there will be no more than logL steps.

Time: O(mlogLlogn); solution.

555E - Case of Computer Network

First of all, let's reduce this problem to a problem on a tree. In order to achieve this let's orient edges in all biconnected components according to a DFS-order. We'll get a strongly connected component. Suppose it's false. Then this component can be divided into parts A and B such that there's no edge from B to A. As initially there are at least two edges between A and B this situation is impossible because after entering B in our DFS we'll have to exit via one of these edges. Contradiction. We can compress all biconnected components.

Now we need to handle several queries "orient edges on a simple path in a tree" and to check if there are no conflicts. For this let's hang our tree and find LCA's for queries' pairs of vertices. Start another DFS and for every subtree count vertices in this subtree that are beginnings of queries' paths (call it a), that are ends of queries' paths (call it b) and that are precalculated LCAs (call it c). Now we can orient the edge connecting the root of the subtree and its parent: if a - c is positive then it should be oriented up, if b - c is positive then it should be oriented down, if both are positive there's no solution, if both are zeros the direction does not matter.

Time: O(n + qlq) where lq is the time of calculating LCA per query; solution that uses slightly other method for the last part.

  • Vote: I like it
  • +84
  • Vote: I do not like it

Comments Comments (77)
| Write comment?
»
9 years ago, # |
  Vote: I like it +28 Vote: I do not like it

LoL that's just inviting downvotes

→ Reply
»
9 years ago, # |
← Rev. 2   Vote: I like it +102 Vote: I do not like it

Actually I am interested why not to prepare editorial before the contest?

P.S. Of course, not to publish editorial before the contest, but simply write it and save in drafts.

→ Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it +7 Vote: I do not like it

    And I am interested why doesn't anybody post their solutions. I don't force somebody to post a solution, I just mean that every editorial some people submited different code and concept, but now all quiet. Strange things.

    → Reply
    • »
      »
      »
      9 years ago, # ^ |
        Vote: I like it +2 Vote: I do not like it

      I agree with you

      So let me start with Problem B:

      For each gear, calculate minimum number of rotations which will get the required active tooth

      Answer is Yes if all gears require the same number of rotations

      Else, answer is No

      → Reply
      • »
        »
        »
        »
        9 years ago, # ^ |
          Vote: I like it +2 Vote: I do not like it

        Alternatively, since the limits were relatively small, (N < 1000), an O(N^2) solution would work fine, so you could instead simulate pressing the button N times, then checking to see if it works each time

        → Reply
      • »
        »
        »
        »
        9 years ago, # ^ |
          Vote: I like it +1 Vote: I do not like it

        Or, you could define the button operation, and call it until the first gear has the 0th as the active tooth, once this is the case, if any a[i] != i => "No" if all a[i] == i => "Yes"

        → Reply
»
9 years ago, # |
  Vote: I like it +17 Vote: I do not like it

Div1 A was a bit confusing

→ Reply
»
9 years ago, # |
← Rev. 5   Vote: I like it +3 Vote: I do not like it

Hi there! Although I couldn't get it through in the contest, here's my solution for Div2D/Div1B:

  • Define gap as gap[i] = L[i+1]-R[i].

  • Sort all the gaps in non-increasing order.

  • Put all the bridges in a map, so that we can apply binary search on them.
  • Starting from the largest gap, do:

— Define min_gap : The actual gap between adjacent islands = L(i+1)-R(i)

— Define max_gap : The difference R(i+1)-L(i), that is the maximum size of the bridge allowed.

— Extract the largest bridge available in range[min_gap,max_gap] and use bridging this gap.

— If no such bridge is available, output "No".

  • Done.

Here is a link to my AC solution. : http://codeforces.me/contest/556/submission/1180956

→ Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Can we sort gaps in increasing order and extract smallest bridge in range[min_gap,max_gap]? I used this approach but got wrong answer on test case #6(may be implementation error).

    → Reply
    • »
      »
      »
      9 years ago, # ^ |
      ← Rev. 2   Vote: I like it 0 Vote: I do not like it

      Yes, it is correct because of the following invariant that is maintained: The bridge we have extracted will be :

      a) The list of available bridges for this gap, as [min_gap,max_gap] is the range of bridges available for this gap.

      b) So we will in any case have to choose one of these. Since all the gaps after this are less than this gap, therefore these bridges will fit them too. It makes sense to choose the largest available possibility as this way we will minimize the chance of "choosing the wrong bridge" later on.

      EDIT: Sorry, I misread your comment. No that would be incorrect as explained by @crew_underfog_p1. I have clarified above as to why sorting it in non-increasing order works.

      → Reply
      • »
        »
        »
        »
        9 years ago, # ^ |
          Vote: I like it +1 Vote: I do not like it

        The forward approach should be wrong as per my understanding. Consider there is a gap1 with mn,mx = (1,10) and there is another gap2 with mn,mx = (2,3) and the bridges available are 2, 8. So according to your greedy allotment, the leftmost gap i.e gap1 will be alloted 2 and the gap2 cannot be allotted 8. This would lead to WA. A similar scenario should occur in backward approach unless you re using swaps as mentioned in the editorial. Please correct me if I have misunderstood.

        → Reply
    • »
      »
      »
      9 years ago, # ^ |
        Vote: I like it +2 Vote: I do not like it

      I had the same WA in test #6, notice that FoolForCS solution process the gaps in decresing order

      → Reply
»
9 years ago, # |
  Vote: I like it +10 Vote: I do not like it

I solved Div1 C without any segment tree but unfortunately I have not solved it in contest.

→ Reply
»
9 years ago, # |
  Vote: I like it +5 Vote: I do not like it

Lord_F : Editorial's source code link is not working. Can you fix that. ?

→ Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Oops. Will fix this.

    → Reply
    • »
      »
      »
      9 years ago, # ^ |
        Vote: I like it -15 Vote: I do not like it

      Still not working.

      → Reply
      • »
        »
        »
        »
        9 years ago, # ^ |
          Vote: I like it +27 Vote: I do not like it

        Still not fixed. I'll do it momentarily after I post the remaining problem editorial

        → Reply
      • »
        »
        »
        »
        9 years ago, # ^ |
          Vote: I like it +10 Vote: I do not like it

        Fixed now =)

        → Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

I got several WA's on Div. 1 A before the problemsetters rewrote the descriptions (thank you! :P), but I was still failing on pretest #6, and it was 5 minutes before the end of the contest that I realized that 1 → 2 → 4 → 5 means '1 in 2 in 4 in 5' (5 is the one outside while 1 is the one which doesn't contain anything else). I thought it meant '5 in 4 in 2 in 1'... (And of course I didn't solve this A :( )

So I'd like to ask the descriptions to be made clearer again. Would it be possible to say 'for example, 1 → 2 → 4 → 5 (where 1 is in 2, 2 is in 4, and 4 is in 5)' in the problem? Thank you in advance.

Despite, the problem itself is really a nice one, which requires mathematical thinking & ideas rather than complex implementations. A good Div. 1 A :)

→ Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Quote from the statement: A matryoshka with a smaller number can be nested in a matryoshka with a higher number

    → Reply
    • »
      »
      »
      9 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Oh sorry... I paid too much attention to the numbers... Well, that's my fault. The arrows may really be misleading sometimes, though.

      → Reply
»
9 years ago, # |
  Vote: I like it +4 Vote: I do not like it

in div1-B/div2-d it's written that" Now we have a well-known problem: there are n - 1 segments and m points on a plane, for every segment we need to assign a point which lies in it to this segment and every point can be assigned only once."

Can someone please tell me what this problem is popularly known as or give link to some valuable resource related to the problem??

→ Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it +3 Vote: I do not like it

    Maybe I'm wrong about that one. When I was given this problem I already knew such greedy solution, so I thought it actually is well-known.

    → Reply
    • »
      »
      »
      9 years ago, # ^ |
        Vote: I like it +4 Vote: I do not like it

      Could you give more valuable resource about this problem ? Thanks

      → Reply
»
9 years ago, # |
  Vote: I like it -7 Vote: I do not like it

Problem B div 1 was very good ! I hope more interesting problem like this :)

→ Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

case of chocolates:

can explain output in this test case?(test case 5)

input:

10 10 5 6 U 4 7 U 8 3 L 8 3 L 1 10 U 9 2 U 10 1 L 10 1 L 8 3 U 8 3 U

output: 6 7 3 0 10 2 1 0 0 0

→ Reply
»
9 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

For problem 555-C I like the segment tree approach but I would be interested in knowing how some people did it using set and map . If someone who solved the problem using set could let me know I would appreciate it .

→ Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it +21 Vote: I do not like it

    Here is a way of doing it with map. Consider two different maps: one storing the left events and one storing the up events. These maps take the x-coordinate of the query and map it to the answer.

    Add (0, n + 1) and (n + 1, 0) to the triangular grid of points and query both of these points going up and left. These points will now be in both maps.

    Suppose that there is a new query (x, y). Suppose that this query is to the left (the up case is similar). If (x, y) was already queried, then the answer is 0. Or else, let g < x be the greatest integer so that (g, n + 1 - g) was a left query (such a thing exists because 0 is in the left map). The query for (g, n + 1 - g) can reach to a certain x-coordinate h. It is easy to see that (x, y) can also reach to at most h (draw a few diagrams and you will see).

    In order for this to not be the answer, (x, y) must have been queried as an up event or some up event between g and x cuts the line from (x, y) off. This can easily be checked by querying the up map.

    Link to solution: http://codeforces.me/contest/555/submission/11803362

    → Reply
  • »
    »
    9 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    edit : ok I found the problem with the approach I wrote earlier.

    → Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    A simple solution with set:

    The key observation is that each query simply breaks the problem into two similar sub-problems, which in general look like:

          ### ^ 
      ### h
      ### v
######@@@
######@@
######@
<--w->

    (for the starting state w=h=0). We will maintain an ordered set of such sub-problems. Each sub-problem consists of an interval on the diagonal and two parameters w,h. The ordering will be by interval coordinate, let's say x, so that given a query with coordinate x we can quickly get the sub-problem from the set.

    Given a sub-problem and a corresponding query it's easy to split the sub-problem into two subproblems and put them back to the set.

    Complexity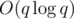 . Submission

    → Reply
»
9 years ago, # |
  Vote: I like it +7 Vote: I do not like it

I think all of the problems were really interesting! I hope we'll see more contests from you two! :)

→ Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Was it just me or atleast before the announcement in Div1 A/Div2 C someone thought of applying union-find?

→ Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it +9 Vote: I do not like it

    Honestly, the announcement was more like an explanation, not a modification. I understood the problem statement before the announcement.

    → Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

The test data of Div.B is not perfect, my code passed but it's wrong. Here is my wrong but accepted submission 11799654, And this is the data in: 3 1 1 2 3 4 5 6 2 out: No

I hope it can be added as a test data.

→ Reply
»
9 years ago, # |
← Rev. 2   Vote: I like it +4 Vote: I do not like it

The test data of Div1.B is not perfect, my code passed but it's wrong. Here is my wrong but accepted submission 11799654, And this is the data in: 3 1 1 2 3 4 5 6 2 out: No

My code output "Yes".

I hope it can be added as a test data.

→ Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it +11 Vote: I do not like it

    I'm sorry to post the message twice indeliberately because my web condition is not very well.

    → Reply
»
9 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

sorry, i misread the problem statement.

→ Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    I didn't use y and I got accepted too and the reason is quite simple: since the statement indicates that xi + yi = N+1, you really don't need to use y anyway once you have x and N.

    → Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can someone please explain 555E solution to me? I didn't understand the editorial.

→ Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it +5 Vote: I do not like it

    First, notice that it is always possible to orient the edges inside a biconnected component such that there is a path between any two vertices. This is evident from the algorithm of finding those components — simply orient the edges in the direction you first discover them in, and the criterion that you check inside the DFS will ensure that it is always possible to find the way back in the tree.

    Next, you condense the tree — that is, replace every biconnected component with a single vertex, and the bridges in the original tree will be the edges of the new tree. The problem is now reduced to orienting edges in a tree. There are multiple ways to proceed from here, I'll give mine.

    You need to find the LCA (least common ancestor) for every query pair (you probably need to do this regardless of which method you choose to solve the problem). Now, for every pair A, B, if their LCA is C, we know that the only path from A to B is to go up from A to C, then down from C to B, so the edges along the way have to be oriented accordingly. Now, if the distance between A and C is X, we will say that from A, at least X edges above it have to be oriented upwards (and vice versa for B). Then we can go through the entire tree from bottom to top, calculate this N as a maximum of the value stored in the node, and values for all children — 1, both for upwards and downwards requirements. If both values are positive, we output No.

    Don't forget that there might be multiple trees if the original graph is not connected. If the original queries are from different components, you'll notice that when calculating their LCA, for instance.

    → Reply
    • »
      »
      »
      9 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Thanks! I get it now.

      → Reply
    • »
      »
      »
      9 years ago, # ^ |
        Vote: I like it -7 Vote: I do not like it

      Well, You are a little wrong in your definitions above.

      The tree formed by compressing the components distinguished by the bridges is different from the block-cut tree formed by compressing the biconnected components of the graph. Also, the components referred above will NOT be biconnected components.

      Eg : Consider the following graph with 5 Nodes and 6 edges
      1 2
      2 3
      3 1
      3 4
      4 5
      5 3

      Here, If we consider the biconnected components , there will be two different biconnected components A and B, having the following nodes
      A --> 1 , 2 , 3
      B --> 3 , 4 , 5

      while there would be only 1 single bridge component (the components referred above) consisting of all the 6 nodes, coz there are no bridges in the graph.

      Refer this for more info about Bridge Tree : http://threads-iiith.quora.com/The-Bridge-Tree-of-a-graph

      In a graph, the biconnected components are distinguished by the Articulation Vertices while the bridge components are distinguished by the bridges.

      Also, if we assign direction to edges inside a bridge component, it will form an SCC, coz each bridge will be a part of a cycle (imagine creating a Spanning Tree of the bridge component and add edges one by one compressing the cycle each time into a single node untill the whole tree is compressed into a single component)

      The above problem can also be solved by forming the Block-Cut Tree by shrinking the BCC's , but it's important to note the distinction between the two different types of tree's.

      Here is an accepted solution using the Bridge Tree approach .
      http://codeforces.me/contest/555/submission/11884660

      → Reply
      • »
        »
        »
        »
        9 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        Oh, yeah by biconnected components I meant the ones where you can connect any pair of nodes with two edge-distinct paths (as opposed to vertex-distinct), guess that's not what it normally stands for.

        → Reply
      • »
        »
        »
        »
        9 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        Well, I believe Rivx is not wrong, you just call things differently. In the editorial I use "biconnected components" exactly as the bridge component. In Russia in order to specify the difference we might use either "edge-biconnected component" or "vertex-biconnected component".

        → Reply
        • »
          »
          »
          »
          »
          9 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          Ok. Didn't know about the terminology used in Russia , because everywhere on the internet, Biconnected components refer to the vertex-biconnected components.

          → Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Why is La ≤ xi - xi - 1 in D? If we have pegs at 1, 2, 3 and 10, and start at 2 with length 5, then we will loop around 3 and come back to 1, no?

→ Reply
  • »
    »
    9 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    Yeah, unfortunately I forgot about this case: this inequality doesn't hold at the first iteration. Fixed this.

    → Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Auto comment: topic has been updated by Lord_F (previous revision, new revision, compare).

→ Reply
»
9 years ago, # |
← Rev. 5   Vote: I like it 0 Vote: I do not like it

I am not able to understand the solution discribed for problem 555A - Case of Matryoshkas

The editorial states the answer is 2n - k - 2L + 2 , which is simply wrong for the test case

3 2
2 1 2
1 3

n = 3
k = 2
l = 2

so

ans = 2*3 - 2 - 2*2 + 2 = 2

whereas the answer is 1

Should'nt it be 2n - k - 2l + 1 ?

If anybody could point what's wrong in my submission : 11800309 , getting WA at pretest 13.

→ Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    It's already fixed. Sorry)

    → Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    You should add break in else branch of if inside two REPs. Try to test on 1 2 3 6 4 5 — in this case you'll count 4 5 as one matryoshka, which is wrong since you can't take a matryoshka from the one which is inside another matryoshka.

    → Reply
»
9 years ago, # |
← Rev. 3   Vote: I like it 0 Vote: I do not like it

i have a question about d problem .

-> "And either i = 1 or La ≤ x(i) - x(i - 1) so it won't also rotate around a peg to the left to peg i."

he sad if La ≤ x(i) - x(i - 1) then "we can skip through several steps momentarily".

but he didn't explain if La >= x(i) - x(i - 1). can anyone answer ?

there are three situations. 1. is the end of the rope between i and j 2. is the end of the rope between i-1 and i 3. is the end of the rope between (<i-1) and i-1

if we are in 1. situation. the La will be at most half of his length if we are in 2. situation. "we can skip through several steps momentarily". if we are in 3. situation. (no answer)

→ Reply
  • »
    »
    9 years ago, # ^ |
    ← Rev. 2   Vote: I like it +8 Vote: I do not like it

    I already mentioned it in the comments. Note that it is only possible at the start, so you only need to check for this situation once per query (and it only takes one extra step). I.e. If you didn't start at i, this situation is impossible.

    → Reply
»
9 years ago, # |
← Rev. 2   Vote: I like it +1 Vote: I do not like it

I wrote up a solution for Div2 D which I think is easier to implement and has been discussed in the comments.

Any comments are more than welcome :)

→ Reply
  • »
    »
    9 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    Thank your for your effort. Could you please explain more your phrase "Specifically, if we sort the gaps based on their max_d, we get the nice property that we will take care first of the gaps with smaller separation while still giving priority to those with smaller min_d." ?

    → Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

I am getting wrong answer on test case 38 of 555D. Any help would be appreciated. Here is my solution.

→ Reply
»
9 years ago, # |
← Rev. 3   Vote: I like it +16 Vote: I do not like it

555E — Case of Computer Network

The solution posted on paste.ubuntu.com with link present in this article is wrong.

Take this test:

14 13 2
1 2
1 3
2 4
3 4
5 6
7 8
7 9
9 10
9 11
11 12
12 13
12 14
13 14
7 10
11 7

It outputs "Yes" instead of "No".

→ Reply
  • »
    »
    9 years ago, # ^ |
    ← Rev. 4   Vote: I like it 0 Vote: I do not like it

    I've found my mistake (hopefully, the only one): there was a problem with initialization of parents while compressing biconnected components which lead to incorrect LCA finding. Now the solution must be correct.

    Actually, I have a solution which uses Tarjan LCA algorithm so answers to all tests from the testset are correct.

    → Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can you please explain me div1 C?

→ Reply
»
9 years ago, # |
  Vote: I like it +3 Vote: I do not like it

Does implicit segment tree mean that we only assign children to nodes when they are needed, in a lazy manner ? It kinda reminds me of trie. Is that right ?

→ Reply
  • »
    »
    9 years ago, # ^ |
    ← Rev. 2   Vote: I like it +4 Vote: I do not like it

    Yes, it does. In the second solution given for Div1 C children in the segment tree are created only when they are needed in lines 65-69.

    → Reply
    • »
      »
      »
      9 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      I think you meant Div1 C. Thank you it helped me a lot.

      → Reply
    • »
      »
      »
      9 years ago, # ^ |
      ← Rev. 2   Vote: I like it 0 Vote: I do not like it

      I'm having trouble coding the implicit segment tree. Could please point out my mistake if you had anytime to spare ? Thank you very much.

      I'm getting TLE on 10th .

      Submission

      I am using indices instead of explicit left and right pointers (and an array of nodes instead of creating new nodes on the fly).

      → Reply
      • »
        »
        »
        »
        9 years ago, # ^ |
          Vote: I like it +1 Vote: I do not like it

        I believe your get is strange: you can visit a node even if q is not in [l;r].

        → Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

In the solution code of problem Case of Computer Network in editorial, what is the purpose of function compress(int v, int cid) ?

→ Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    It finds biconnected components and condensates them.

    → Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Could somebody explain me DIV 2E/DIV 1 C ? I am unable to understand it. I was looking for a clean code in all java submissions and it's one of the cleanest http://codeforces.me/contest/555/submission/11839184 , but I am still unable to understand it, especially those two lines

X.put(n - le.getValue() + 1, X.floorEntry(n - le.getValue() + 1).getValue());
X.put(x, x);

I'd be very grateful if somebody helps me. I spend couple of days without any result.

→ Reply
  • »
    »
    9 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    The short version of Case of Chocolate requires quite a bit of observations (and proofs).

    You cannot understand it through the code itself.

    The short explanation is that you only need to look at 1 of your neighbors to tell the result.

    → Reply
    • »
      »
      »
      9 years ago, # ^ |
      ← Rev. 2   Vote: I like it 0 Vote: I do not like it

      Sorry, but it doesn't help at all

      → Reply
      • »
        »
        »
        »
        9 years ago, # ^ |
        ← Rev. 3   Vote: I like it 0 Vote: I do not like it

        Sorry for giving a short answer there. It's not easy to explain.

        Consider treating each bite as an entry and assume we bit 2 already ('U' from (0, n + 1) and 'L' from (n + 1, 0)).

        Let's take 'U' for instance. Suppose our starting point is (x, y).
        We need only to look at the entry to our immediate right.

        1. Suppose the entry starts from (x2, y2).
        2. If the entry is 'U' and it reaches (x2, y3), then we can reach (x, y3).
        3. If the entry is 'L' and it reaches (x3, y2), then we can reach (x, y2).

        Similarly with 'L', we only need to look at the entry to our immediate left.

        Now the only thing to consider is how to use an ordered container to store the entries.

        → Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Hi, Can someone please tell me how would the Go About 555B — Case of Fugitive if the question was to find the number of ways the bridges can be assigned modulo MOD ?

Thanks :)

→ Reply
»
5 years ago, # |
  Vote: I like it 0 Vote: I do not like it

If anyone's getting a Wrong Answer on Div1 D, consider the following situation: You are trying to rotate the rope so that it gets attached to some peg on the right side. But, if all pegs on the right side are too far off, it won't get attached to any peg on the right and will keep moving and might get attached to some peg on the left.

The following test case may be helpful:

Input
Output

To correct this, 2 things may be done:

  1. Note that this case may only arise while performing the starting move, so you perform the first 2 moves beforehand (2 because the 1st one may not work as in the example above). Code

  2. You consider attaching it to a peg on one side and if that doesn't succeed (you end up at the same peg), try attaching it to a peg on the opposite side. If that too doesn't work, current peg is the answer. Code

→ Reply