Помогите, пожалуйста, решить задачу "Женитьба" с X Жаутыковской олимпиады. Условие

Я нашел разбор этой олимпиады, но я его не понимаю :(

В разборе написано, что алгоритм Куна работает за 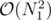(разве не за ?)

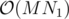Если закрыть на это глаза, то я понимаю оценку 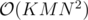: перебираем отрезки за 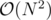и поверяем за 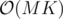Куном.

Но как получить из 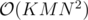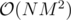я не понимаю. Если применить идею, что если какой-то отрезок подходит, то подойдут все отрезки, содержащие его, то мы получим оценку .

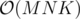Что происходит в последней части разбора я вообще не понял.

Теперь о том, как делал я.

Запустим плавающее окно. Проверять будем с помощью Диница, который должен находить паросочетание быстрее Куна (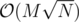 против 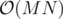). Но мы не будем каждый раз строить граф и находить паросочетание заново. При сдвиге правой границы добавим ребра в граф, а при сдвиге левой удалим ребра из графа, при этом откатим поток, который проходил по этим ребрам (наверное, что-то похожее имелось в виду в последней части разбора).

За сколько эта ерунда будет работать, я понятия не имею, но берет 62/100.

Как решить эту задачу? Имеет ли смысл использовать здесь Диница вместо Куна?

Есть массив чисел. Как быстро отвечать на запросы

• прибавить число на отрезке
• узнать сколько раз число встречается на отрезке?

Пока что ничего быстрее не придумал.

Если кому интересно, идея sqrt-декомпозиции:

• разобьем массив на блоков
• для каждого блока будем хранить
  • cnt[x] — количество чисел x в блоке
  • delta — число, которое надо прибавить ко всем числам в этом блоке

Тогда на запрос прибавления числа D на отрезке будем отвечать так:

• Если блок полностью входит в отрезок, то изменим его delta на D

• Иначе пройдемся по элементам, которые лежат в границах запроса, и просто добавим к ним D

  cnt[a[i]] --;
  a[i] += D;
  cnt[a[i]] ++;
  

Запрос о количестве чисел X на отрезке:

• Если блок полностью входит в отрезок, просто вернем cnt[X - delta]
• Среди остальных элементов учтем те, которые равны X - delta

Решил задачу 427D - Расшифровка сигнала с помощью суффиксного дерева. Однако мое решение за O(N) (6579114) работало дольше, чем решения за O(n²) — 717 мс и кушало ~200 мб памяти!

Сразу нашелся тест, на котором локально это решение работало долго (около 5,8 секунды!!!):

aaa...aa

aaa...aa

Стал разбираться. Выяснилось, что по ходу построения дерева, создается ~12,5 млн. позиций в дереве (объект, который указывает на вершину в сжатом боре). Эти объекты я создавал в куче, через new. Это удобно тем, что можно вернуть указатель на NULL (например, при попытке перехода из вершины по символу).

Я, конечно, знал, что выделение памяти в куче работает дольше, чем на стеке, но не в 15 же раз! :) Вообще, изначально я хотел избавиться от new из-за лишнего потребления памяти: в каждой позиции хранится указатель на вершину(4 байта) + номер буквы на ребре(4 байта) * 12,5 млн.  ≈  100 мб.

В итоге без использования new мое решение получило AC (6579111) за 171 мс, при этом потребляя 2 мб памяти.

У меня только 2 вопроса:

Почему 200 - 100 = 2

И почему локальное время выполнения так сильно отличается от серверного(без new стало работать быстрее на 1 секунду, но 4,8 и 0,17 — все же большая разница)

Заранее спасибо

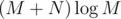Написал решение(6479167) на задачу "Вставка ключевых значений"(Тренировка СПбГУ B #10 Декартово дерево Light), у которого асимптотика , но, видимо, с громадной константной, ибо TL 37.

Решение заключается в следующем: будем честно хранить несуществующие элементы в виде нулей, а также запомним их позиции. Т.е. сначала у нас будет декартово дерево по неявному ключу с M нулями и set с их позициями(1, 2 ... M).

Теперь, чтобы обработать Insert(i, k), мы найдем в сете позицию самого первого нуля, начиная с i-той позиции, и, если такая позиция существует, удалим его из сета и декартова дерева. Осталось только вставить k на позицию i.

Такое решение валится тестом

131072 131072
1 1 1 ... 1 1 1

На нем у меня работает 5,5 секунды

Это у меня руки кривые, или существует более адекватное решение?

Я умею обрабатывать запросы типа "изменить значение в вершине", посчитать что-то на пути.

А как изменять значение на ребре? Есть идея хранить в вершине вес ребра из вершины в ее левого сына (в Splay tree). Но тогда возникает проблема с изменением корня дерева: при реверсе ребер, значения в вершинах будут неправильными, и придется как-то пропихивать веса в левого сына.

Подскажите, пожалуйста, как правильно хранить и изменять вес ребра в Link-cut tree?

Upd. Обновил картинку

Upd2. Только что нашел: http://www.cs.princeton.edu/~rwerneck/docs/TW07.pdf

The obvious implementation of the ST-tree interface is to store with each node its value and a pointer to its parent. This supports link, cut, parent and findcost in constant time, but evert, findroot, findmin and addcost must traverse the entire path to the root. Despite the linear-time worst case, this representation might be good enough for graphs with small diameter, given its simplicity. We tested two variants of this implementation, lin-v and lin-e; the former associates costs with vertices, the latter with edges. Both store values at vertices, but lin-e interprets such a value as the cost of the arc to the parent (the values must be moved during evert).