Hi everyone!
I'm currently trying to write an article about $$$\lambda$$$-optimization in dynamic programming, commonly known as "aliens trick". While writing it, I stumbled upon a fact which, I believe, is a somewhat common knowledge, but is rarely written out and proved explicitly. This fact is that we sometimes can repeatedly use ternary search when we need to optimize a multi-dimensional function.
Thanks to mango_lassi for a useful discussion on this and for counter-example on integer ternary search!
$$$1$$$-dimensional search
Def. 1. A function $$$f : X \to \mathbb R$$$, where $$$X \subset \mathbb R$$$, is called unimodal if there is a segment $$$[L, R]$$$ such that $$$f(x)$$$ strictly decreases on $$$(-\infty, L] \cap X$$$, strictly increases on $$$x \in [R,+\infty) \cap X$$$ and is equal to its global infimum on $$$x \in [L, R] \cap X$$$.
Ternary search is a family of similar algorithms that allow to estimate the infimum value of a unimodal function $$$f: X \to \mathbb R$$$ on a continuous segment of arguments by splitting it into $$$3$$$ roughly equal parts and reducing the search to at most $$$2$$$ of these parts.
The algorithm takes a segment $$$[l,r]$$$ as an input and chooses two points $$$x_1, x_2 \in X$$$ such that $$$l \leq x_1 < x_2 \leq r$$$. If $$$f(x_1) < f(x_2)$$$, the segment is reduced to $$$[l, x_2]$$$ and otherwise it's reduced to $$$[x_1, r]$$$.
The algorithm stops when a certain condition is met, typically when $$$r-l \leq \varepsilon$$$ or when a certain number of iterations is met.
Multi-dimensional unimodality
Def. 2. A set $$$X \subset \mathbb R^c$$$ is called convex if for all $$$x_1, x_2 \in X$$$ and all $$$\lambda \in [0, 1]$$$ it contains $$$x_1 + \lambda[x_2 - x_1]$$$.
Let $$$X \subset \mathbb R^c$$$ be a convex set. There are two most common ways to generalize unimodality on higher dimensions.
Def. 3. A function $$$f: X \to \mathbb R$$$ is called convex if for any $$$x_1, x_2 \in X$$$ and any $$$\lambda \in [0, 1]$$$, it holds that
Def. 4. A function $$$f: X \to \mathbb R$$$ is called strictly quasi-convex if for any $$$x_1, x_2 \in X$$$ and any $$$\lambda \in (0, 1)$$$, it holds that
It is possible to prove that a $$$1$$$-dimensional convex or strictly quasi-convex function is also unimodal. Moreover, all unimodal functions for which $$$L=R$$$ (infimal segment has a zero length) are also strictly quasi-convex, so these classes are almost equivalent on $$$\mathbb R$$$.
However, convexity and strict quasi-convexity do not imply one another. For example, $$$\max(1, |x|)$$$ is convex, but not strictly quasi-convex. On the other hand, $$$\sqrt{|x|}$$$ is strictly quasi-convex, but not convex. Ternary search would work on both of these functions.
Note that $$$f(x)$$$ must be strictly decreasing until it reaches minimum value and after the minimum value segment it must be strictly increasing for this to work. Otherwise it would be impossible to choose a correct segment reduction for $$$f(x_1)=f(x_2)$$$. This also means that non-strict quasi-convexity is not enough, as $$$\text{floor}(|x|)$$$ is quasi-convex and has segments of equal values other than $$$f(x^*)$$$.
Multi-dimensional search
Sometimes it happens that we need to minimize $$$f : X \times Y \to \mathbb R$$$, where $$$X, Y \subset \mathbb R$$$. If it is somehow possible to minimize $$$f_{x}(y)=f(x, y)$$$ for a fixed $$$x$$$, we might do a ternary search of $$$x$$$ over the function
Typically, the minimization of $$$f_{x}(y)$$$ is, in turn, computed with a nested ternary search. For this algorithm to deliver an actual global minimum of $$$f$$$, we need $$$h$$$ and each of $$$f_{x}$$$ for every possible $$$x$$$ to be quasi-convex.
Sometimes, it is possible to prove it directly. Another possible way to go here when $$$X$$$ and $$$Y$$$ are convex is to prove the quasi-convexity of $$$f(x,y)$$$ as a multi-dimensional function, which would also yield a quasi-convexity of $$$h$$$ and $$$f_x$$$.
When $$$X$$$ is convex, quasi-convexity of $$$f:X \to \mathbb R$$$ means that for any distinct $$$x_1, x_2 \in X$$$ and any $$$x \in (x_1, x_2)$$$ it holds that
$$$f_x$$$ is quasi-convex by definition, as it is equal to $$$f(x, y)$$$ on the interval between $$$(x,y_\min)$$$ and $$$(x, y_\max)$$$. As for $$$h$$$, let $$$x_1, x_2 \in X$$$ and let $$$y_1$$$ and $$$y_2$$$ to be optimal $$$y$$$ for $$$h(x_1)$$$ and $$$h(x_2)$$$. The interval between $$$(x_1, y_1)$$$ and $$$(x_2, y_2)$$$ contains a point $$$(x,y)$$$ such that
for every possible $$$x \in (x_1, x_2)$$$. Similarly, one can prove that $$$h(x)$$$ preserves convexity, that is, $$$h(x)$$$ is convex if $$$f(x, y)$$$ is.
The function $$$h(x)$$$ defined above is called an infimal projection of $$$f(x, y)$$$ onto $$$X$$$. Alternative, perhaps more intuitive way to see why $$$h(x)$$$ is convex is to notice that the epigraph of $$$h(x)$$$ is a projection on the $$$xOz$$$ plane of the epigraph of $$$f(x, y)$$$.
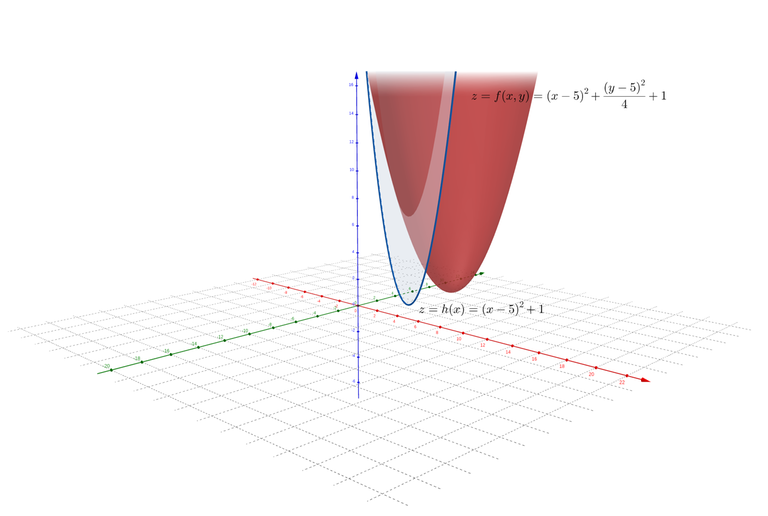
Below is the illustration. For $$$f(x, y) = (x-5)^2+ \frac{(y-5)^2}{4}+1$$$, its infimal projection is $$$h(x) = (x-5)^2+1$$$.
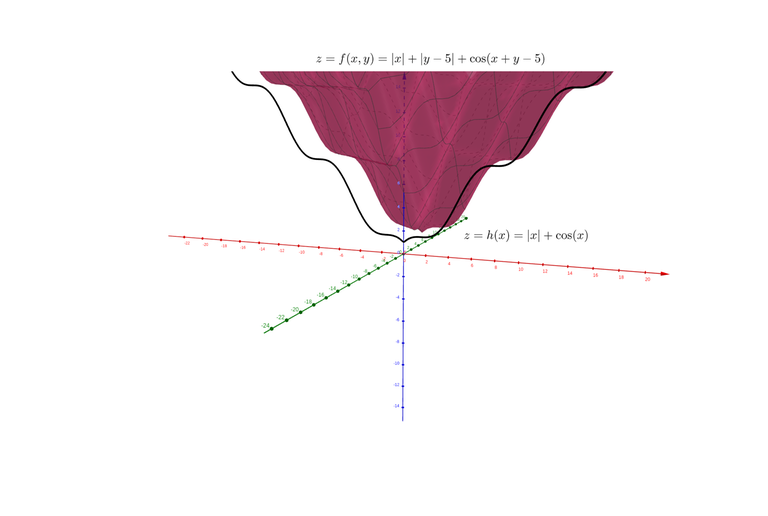
Another illustration with a non-convex function: $$$f(x, y)=|x|+|y-5|+\cos(x+y-5)$$$, $$$h(x)=|x|+\cos x$$$.
Caveat
Convexity and strict quasi-convexity of $$$f$$$ on $$$\mathbb R^2$$$ don't necessarily imply that ternary search would work on $$$\mathbb Z^2$$$. Let
The function $$$f$$$ is convex and strictly quasi-convex on $$$\mathbb R^2$$$. However, in small integers $$$h(2k) \approx 0$$$ and $$$h(2k+1) \approx \frac{1}{4}$$$, thus the function is neither convex nor uni-modal. It doesn't mean that ternary search is never applicable to integers, however you would need to be extra careful and prove directly that $$$h$$$ and $$$f_x$$$ are uni-modal to use it.
Open questions
- Are there any problems that are solvable with nested ternary search over integers or any other discrete set?
- Are there any better criterion for ternary search to be applicable in a discrete case, other than proving uni-modality of $$$h$$$ and $$$f_x$$$?
- What would be the most meaningful generalization of binary search on multi-dimensional case? Quasi-linear functions?






