Hi everyone!
I'm currently trying to write an article about $$$\lambda$$$-optimization in dynamic programming, commonly known as "aliens trick". While writing it, I stumbled upon a fact which, I believe, is a somewhat common knowledge, but is rarely written out and proved explicitly. This fact is that we sometimes can repeatedly use ternary search when we stumble on the optimization of multi-dimensional function.
Thanks to mango_lassi for the discussion and providing counter-examples from "caveats" section!
$$$1$$$-dimensional search
Let $$$X$$$ be a compact subset of $$$\mathbb R$$$, for example $$$X = [L, R]$$$ or $$$X = \mathbb Z \cap [L, R]$$$. A function $$$f: X \to \mathbb R$$$ is called strictly quasi-convex if for any distinct $$$x_1, x_2 \in X$$$ and any $$$x \in (x_1, x_2) \cap X$$$, the following inequality holds:
Less formally, it means that function is uni-modal, i. e. there is a unique point $$$x^*$$$, such that $$$f$$$ strictly decreases up to $$$x^*$$$ and strictly increases afterwards. However, we will stick to this definition, as it naturally generalizes to multi-dimensional case.
A ternary search maintains a sequence of nested segments $$$[L_0, R_0], [L_1, R_1], \dots$$$ such that $$$x^* \in [L_k, R_k]$$$ for every $$$k$$$.
Initial segment is typically chosen as $$$L_0 = \min X$$$ and $$$R_0 = \max X$$$.
To find a segment $$$[L_{k+1}, R_{k+1}]$$$, two points $$$x_1, x_2 \in X$$$ are chosen such that $$$L_k < x_1 < x_2 < R_k$$$. Then, $$$f(x)$$$ is computed in both points. If $$$f(x_1) < f(x_2)$$$ it means that $$$x^* \in [L_k, x_2]$$$ and otherwise it means that $$$x^* \in [x_1, R_k]$$$.
Convexity and strict quasi-convexity do not imply each other. For example, $$$\max(1, |x|)$$$ is convex, but not strictly quasi-convex. On the other hand, $$$\sqrt{|x|}$$$ is strictly quasi-convex, but not convex. Ternary search would work on both of these functions.
Note that $$$f(x)$$$ must be strictly decreasing until it reaches minimum value and after the minimum value area it must be strictly increasing for this to work. Otherwise it would be impossible to choose a correct segment reduction for $$$f(x_1)=f(x_2)$$$. This also means that non-strict quasi-convexity is not enough, as $$$\text{floor}(|x|)$$$ is quasi-convex and has segments of equal values beyond $$$f(x^*)$$$.
Multi-dimensional search
Sometimes it happens that we need to minimize $$$f : X \times Y \to \mathbb R$$$, where $$$X, Y \subset \mathbb R$$$. If it is somehow possible to minimize $$$f_{x}(y)=f(x, y)$$$ for a fixed $$$x$$$, we might do a ternary search of $$$x$$$ over the function
Typically, the minimization of $$$f_{x}(y)$$$ is, in turn, computed with a nested ternary search. For this algorithm to deliver an actual global minimum of $$$f$$$, we need $$$h$$$ and each of $$$f_{x}$$$ for every possible $$$x$$$ to be quasi-convex.
Sometimes, it is possible to prove it directly. Another possible way to go here when $$$X$$$ and $$$Y$$$ are convex is to prove the quasi-convexity of $$$f(x,y)$$$ as a multi-dimensional function, which would also yield a quasi-convexity of $$$h$$$ and $$$f_x$$$.
When $$$X$$$ is convex, quasi-convexity of $$$f:X \to \mathbb R$$$ means that for any distinct $$$x_1, x_2 \in X$$$ and any $$$\lambda \in (0, 1)$$$ it holds that
In this terms, $$$f_x$$$ is quasi-convex by definition. As for $$$h$$$, its quasi-convexity is proven as follows:
This, in turn, due to strict quasi-convexity of $$$f$$$ can be re-written as
because for minimization it is always optimal to use $$$y_1=y_1^*$$$ that minimizes $$$f(x_1,y_1)$$$ and $$$y_2=y_2^*$$$ that minimizes $$$f(x_2,y_2)$$$.
The function $$$h(x)$$$ defined above is called an infimal projection of $$$f(x, y)$$$ onto $$$X$$$.
In a very similar way, it is possible to prove that infimal projection also preserves convexity, that is, $$$h(x)$$$ is convex if $$$f(x, y)$$$ is. This implies, that convexity of $$$f(x, y)$$$ is another condition that allows the use of nested ternary search. Alternative, perhaps more intuitive way to show that $$$h(x)$$$ is convex is to notice that the epigraph of $$$h(x)$$$ is the epigraph of $$$f(x, y)$$$, projected on $$$xOz$$$ plane.
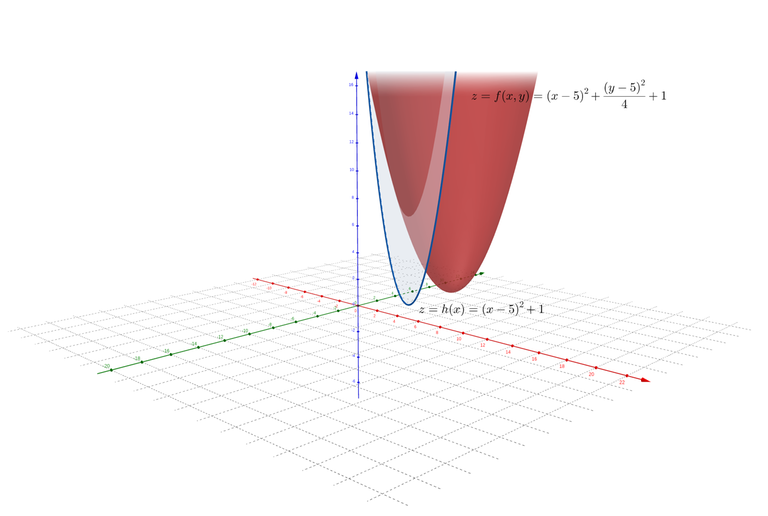
Below is the illustration. For $$$f(x, y) = (x-5)^2+ \frac{(y-5)^2}{4}+1$$$, its infimal projection is $$$h(x) = (x-5)^2+1$$$.
Another illustration with less regular function: $$$f(x, y)=|x|+|y-5|+\cos(x+y-5)$$$, $$$h(x)=|x|+\cos x$$$.
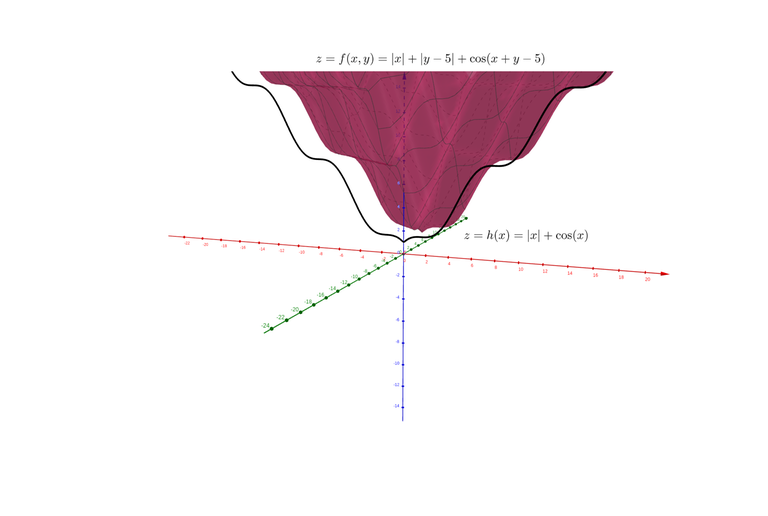
The function is neither convex, nor strictly quasi-convex, yet the fact about epigraphs of functions still holds.
Caveat
Convexity and strict-convexity of $$$f$$$ on $$$\mathbb R^2$$$ don't necessarily imply that ternary search would work on a subset of $$$\mathbb Z^2$$$. Let
The function $$$f$$$ is convex and strictly quasi-convex on $$$\mathbb R^2$$$. Its minimum value is obtained when $$$y=\frac{x-1}{2}$$$ in real numbers, so $$$h(x)=\frac{x+1}{2}$$$. In integers, however, $$$h(0)=0$$$, $$$h(1)=\frac{1}{4}$$$ and $$$h(2)=$$$.






