It is very uncomfortable for us to keep track of Gigi's players. More specifically, it's awkward to note the fact that each second we must update all the blocked positions due to their movement. So, we make the following claim: A pass is unsuccesful if the segment $$$[ (x_1,y), (x_2, y + (x_2-x_1)) ]$$$ intersects any player of Gigi's.

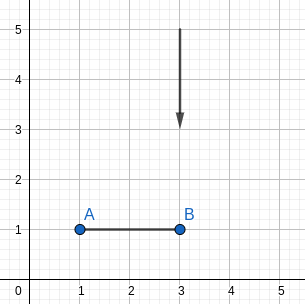
the initial arrangement

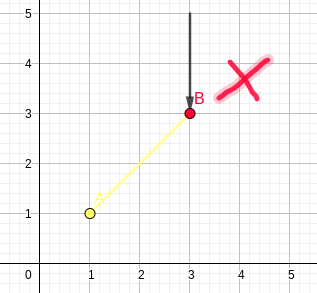
the arrangement, as defined by the ammendement we made earlier

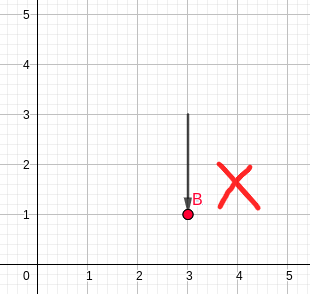
the arrangement at T=2, as defined by the statement

We can prove this by induction. First, when we refer to (a,b)=1 at some time, it means that this point will be blocked at that time.

Base case: $$$(a+1,b), T=1 <=> (a+1,b+1), T=0$$$ (i.e. they are equivalent points at different times)

This derives from the statement, since if $$$(a+1,b+1), T=0$$$, then $$$(a+1-1,b+1), T=1$$$

Inductive step:

applying the base case on $$$(a+x+1,b+x), T=0$$$ we get

then again, by default, we have

So

And

, so

QED

Now, let's assume we have to solve the following problem:

Given some vertical segments, determine for each query consisting of a horisontal segment if this intersects any of the earlier given segments.

This is a classical exaample of a problem that can be solved using the technique of line-sweeping. The solution we know, at least, is the following: sort both the vertical segments and the horizontal ones by their greatest X-coordinate. Then: A vertical segment is an update on all the Y-coordinates it covers. A horizontal segment is a point-query that asks if the latest vertical segment that covers this Y-coordinate happened after the left-X-limit of the segment.

This can be solved using a Segment Tree with lazy propagation.

I do admit that this is a... bad, to say the least, solution for this problem, and there are easier solutions. But I saw this problem and that was the first thing that struck me

The problem is that momentarily we have queries on lines parallel to ( (0,0), (1,1) ), and segments for updates parallel to Oy. With more consideration, we can say that we are currently working in the space defined by

So, we have to transform it to

This can be obviously done by multiplying with the inverse of the first matrix (by the definition of matrixes) and then multiplying it with the latter (which is the identity matrix, so it won't have any effect). The inverse we are talking about is of course:

The effect on this matrix on every vector (which, in our case, would be the endpoints of the segments) in the plane is basically just subtracting the x-coordinate value from the y-coordinate value. So we use this to recalculate the input to the "normal" version. Then we can use the sweep-line algorithm we described earlier to solve the problem.

Time complexity: $$$O((N+M)*(log(N+M)+log(COORDMAX)))$$$

Space complexity: $$$O(N+M+COORDMAX)$$$

I do agree that I might have over-complicated the solution, but all of this was just for rigorous mathematical demonstration purposes. I also note that if we were to give the problem using something of the sorts "passes move with speed X, and players go down with speeds Y", the problem could've easily made it as the easy problem from some Romanian IOI TST (the solution would be to change the first column of the initial transformation to (a,b)). We decided not to do this, because we didn't want to implement Segment trees over doubles, and neither would the contestant in this case. Also, as "artificial" the problem might seem, the idea for the original problem is as you see it in the statement (except the initial problem didn't have the bounds that the passes were horizontal and the blockers were vertical).

Firstly , let $$$sb(n,k)$$$ be the number of ways of writing n as sum of k values greater or equal to 0. This is well known as "Stars and bars".

How can we encode a way of choosing money ? The conditions of a move are as follows :

• From each bag , substract its amount of money by some value which is $$$\ge 0$$$.
• There must exist at least one bag such that we substracted a value $$$> 0$$$ from it.

Thus , we can encode a way of choosing money as follows :

$$$A_{1,1}$$$ $$$A_{1,2}$$$ $$$\cdots$$$ $$$A_{1,k}$$$

$$$A_{1,1}$$$ $$$A_{1,2}$$$ $$$\cdots$$$ $$$A_{1,k}$$$

$$$\vdots$$$ $$$\, \, \, \, \, \, \, \, \, \, \, \, \, \, \,$$$ $$$\ddots$$$

$$$A_{N,1}$$$ $$$A_{N,2}$$$ $$$\cdots$$$ $$$A_{N,k}$$$

$$$\Sigma^{K}_{j=1} A_{i,j} = A_i$$$ for every $$$i$$$ in range $$$[1,N]$$$

There exists an element in every colum of the matrix such that it is $$$> 0$$$.

Where $$$A_{i,j}$$$ is the amount of money we took from bag i , during the j-th move.

Subtask 1 : $$$K = 2$$$

This subtask needs an $$$O(K)$$$ solution. Let's fix the number of 0 values on the first row of the matrix. Let this value be $$$T$$$. Thus , the second row of the matrix must contain at least $$$T$$$ non-zero value. There are $$${K}\choose{T}$$$ ways of arranging the zero values in the first row. This must be multiplied by sb($$$A_1$$$ , $$$K-T$$$) and sb($$$A_2-T$$$,$$$K$$$).We conclude the final formula as being :

Subtask 2 : $$$N,K \le 2000$$$

In this subtask $$$O((N+K) \cdot K)$$$ is required. Let $$$dp_i$$$ be the number of possible configurations which last $$$i$$$ moves. Initially , $$$dp_0 = 1$$$, if all values are equal to 0, otherwise $$$dp_0=0$$$ if there is a value greater than 0. Let's use the principle of inclusion exclusion. First count all configurations , in which there could be a column full of 0s. Their number is equal to

Now we need to subtract from that number , the number of matrices that contain columns full of 0s. Let's use the previous states. It turns out that the number of matrices that contain columns full of 0s is equal to

This is true because we will subtract the number of matrices with 1 column full of 0s, then the ones with 2 columns full of 0s ... So , our transitions are :

Time complexity $$$O((N+K) \cdot K)$$$