Hello, codeforces.
I think this technique is important, and easy to code, although I haven't found much about it, so I've decided to make a blog explaining it.This technique allows to compare substrings lexicographically in O (1) with a preprocessing in O (NlogN).
As this is my first post on codeforces, please let me know if there are any mistakes.
Prerequisites:
- Basic strings knowledge.
- Sparse Table(Optional).
What Dictionary of Basic Factors is?
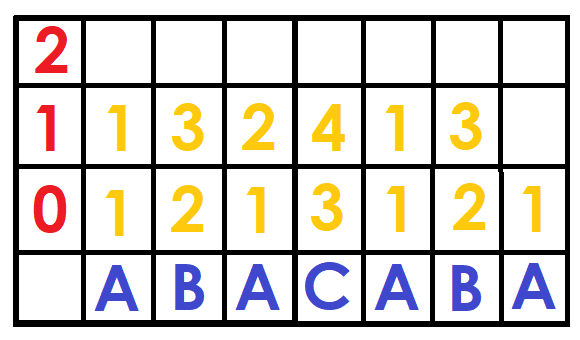
As in the sparse table we will have a matrix of size $$$N\logN$$$ called $$$DFB$$$, where $$$DFB[i][j]$$$ tells us the position of the string $$$S[i ... i + 2^j-1]$$$ (the first time it appears) among all the strings of size $$$2^j$$$ ordered lexicographically.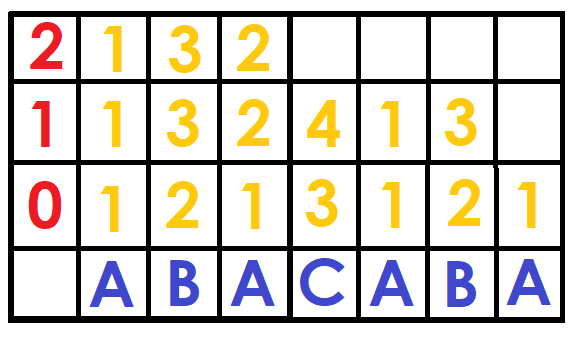
So, how do we build the matrix? Let's start with the lowest level, for powers of size $$$2^0$$$, we simply put the position of the character $$$S[i]$$$ in the dictionary (1 for A, 2 for B ... and so on).
For the following $$$ DFB[i][j] $$$ we can save a pair of numbers that are $$$ (DFB[i][j-1], DFB[i+2^{j-1}][j-1]) $$$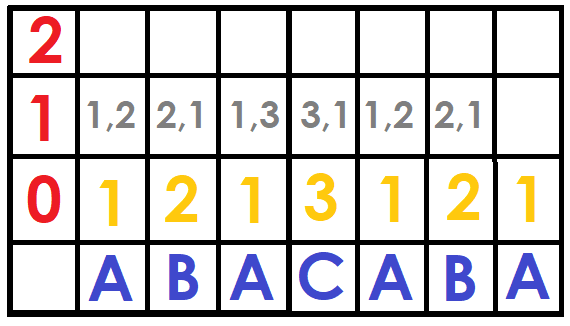
Now we replace the pairs by their position (the first time it appears) in the sorted array of pairs in that power of two