Catalan Numbers is a well known sequence of integers that appear in combinatorics, there is a chance that you might have run into such counting problems and you might have even solved them with DP without realizing that they are a known sequence. Here are a few problems to get us started.
Binary Trees Count
Find the count of different binary trees with $$$n$$$ nodes, we'll denote to that by $$$C_n$$$. This can be solved by observing the substructure of the problem:
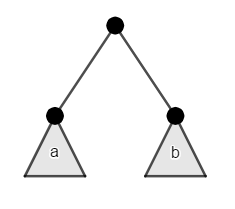
From the root, the left subtree $$$a$$$ can be any binary tree of length $$$x$$$, the right subtree $$$b$$$ can be any binary tree of length $$$y$$$, such that $$$x+y=n-1$$$. With the base case at $$$C_0=1$$$ as the empty tree is a valid tree of size $$$n$$$. This directly gives us the answer by the following recurrence relation: (Segner's recurrence relation)
This really looks like a convolution of catalan numbers, so I will refer to this as the Basic Catalan Convolution. The sequence of numbers $$$C_0, C_1, C_2, ...$$$ is called Catalan Numbers, and for reference they are: $$$1, 1, 2, 5, 14, 42, ...$$$ This gives us a simple $$$O(n^2)$$$ implementation with DP, however can we do better? In fact we can, this simple recurrence formula gives out the same values:
There are a lot of ways to prove this formula, perhaps the most common involves generating functions but I will attempt to prove it using another method. First off though, we will need to learn some different applications of Catalan numbers.
Remember, any time you manage to prove that a counting problem has a solution expressed as a Basic Catalan Convolution, it means this problem has the same solution as all other catalan problems.
Balanced Parentheses count
Find the count of balanced parentheses sequences consisting of $$$n$$$ pairs of parentheses (for example $$$(()(()))$$$ is a balanced sequence of $$$4$$$ pairs). A sequence of parentheses is balanced if each opening symbol has a corresponding closing symbol and they are properly nested, or in layman's terms: a closing bracket never appears before an opening one.
Notice that if you consider opening brackets as a "+1" and closing brackets as a "-1", this problem is bijective to a Dyck word of length $$$2n$$$. A Dyck word is a word of "+1"s and "-1" such that any prefix sum is never negative.
Now, to solve our problem we can think of it using this substructure: "$$$($$$ $$$A$$$ $$$)$$$ $$$B$$$", where $$$A$$$ and $$$B$$$ are themselves valid (possibly empty) parentheses sequences. Let's denote number of pairs of parentheses in $$$S$$$ by $$$|S|$$$. Since we used one pair it follows that: $$$|A| + |B| = n-1$$$. This will make us arrive at the same recurrence relation as before.






