Me and my teammate [user:maverick16,2020-12-19] were doing the Problem **I.Critical Structures**, in this [Problem set](https://drive.google.com/drive/folders/1YyLDdceeanjaaz0MwgLiUmOnitLjTnqO) and this is the [CF Problem page](https://codeforces.me/gym/102835/problem/I).↵
↵
In this problem, we are given a connected graph G and the following terminologies are defined:-↵
↵
1. Critical node: a node in G whose removal disconnects G.↵
↵
2. Critical link: an edge in G whose removal disconnects G.↵
↵
3. Critical component: a maximal set of edges in G such that any two edges in the set lie on a common cycle (A cycle is a set of nodes ⟨v0, v1, . . . , v k−1 ⟩, where k ≥ 4, such that any two consecutive vi−1 and vi for 1 ≤ i ≤ k − 1 have an edge, v0 = vk−1 and vi for 0 ≤ i ≤ k −2 are all distinct).↵
↵
4. Largest critical component: a critical component with the maximum number of edges.↵
↵
We have to find number of critical nodes and critical links, p and q, where p/q is in an irreducible form and are defined as follows :-↵
↵
- p is the number of critical components↵
↵
- q is the number of edges in the largest critical component.↵
↵
Our approach to this problem is :↵
↵
find all the bridges and cut vertices first, remove all the bridges. now apply dfs through individual component and count the edges in that component, we divided this into two cases from here:-↵
↵
1. there a single cut vertex in the component remove it and count both components (components separated by cut vertex) as different↵
2. else take the complete component as a single critical component↵
↵
p will be the number of components counted with this dfs + bridges and q will be max edges in a component.↵
↵
But, this approach should fail, when the graph looks like this, however it passed all tests, can anyone help with this?↵
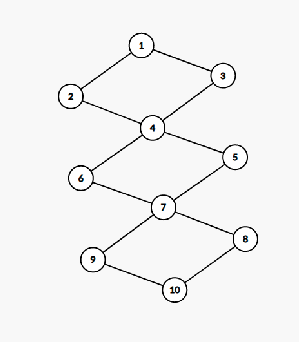↵
↵
<spoiler summary="Expected Output">↵
2 0 3 4↵
</spoiler>↵
↵
<spoiler summary="Our Output">↵
2 0 1 12↵
</spoiler>↵
↵
<spoiler summary="Our Implementation">↵
↵
~~~~~↵
#include<bits/stdc++.h>↵
#define pb push_back↵
#define fast ios_base::sync_with_stdio(false); cin.tie(0); cout.tie(0)↵
#define ll long long↵
#define pii pair<int,int>↵
#define pll pair<ll,ll>↵
#define f first↵
#define s second↵
#define int long long↵
#define sz(x) (ll)(x.size())↵
using namespace std;↵
↵
↵
const int mod = 1e9+7;↵
↵
int expo_pow(int x,int y){↵
if(y == 0) return 1;↵
y=y%(mod-1);↵
x%=mod;↵
if(y==0) y=mod-1;↵
int res=1;↵
while(y){↵
if(y&1) res=(res*x)%mod;↵
x=(x*x)%mod;↵
y>>=1; ↵
}↵
return res;↵
}↵
↵
ll add()↵
{↵
return 0;↵
}↵
↵
template <typename T, typename... Types>↵
T add(T var1, Types... var2){↵
return (((((ll)(var1)) % mod + (ll)(add(var2...))) % mod) + mod) % mod;↵
}↵
↵
ll mul(){↵
return 1;↵
}↵
↵
template <typename T, typename... Types>↵
T mul(T var1, Types... var2){↵
return (((ll)(var1)) % mod * (ll)(mul(var2...))) % mod;↵
}↵
↵
int n,m;↵
vector<vector<int>> adj;↵
int cnt_cric,bridges;↵
vector<vector<int>> adj2;↵
vector<bool> visited;↵
vector<int> tin,low;↵
vector<bool> is_cut;↵
int timer,comp,mx_comp;↵
int cur_comp;↵
int cut_count = 0;↵
vector<vector<bool>> done;↵
↵
void init() {↵
adj.clear();↵
adj.resize(n+1);↵
adj2.clear();↵
adj2.resize(n+1);↵
tin.clear();↵
tin.resize(n+1);↵
low.clear();↵
low.resize(n+1);↵
visited.clear();↵
visited.assign(n+1,0);↵
is_cut.clear();↵
is_cut.assign(n+1,0);↵
done.clear();↵
done.assign(n+1,vector<bool>(n+1,0));↵
cnt_cric = 0;↵
bridges = 0;↵
timer = 0;↵
comp = 0;↵
mx_comp = 0;↵
}↵
↵
void dfs(int v,int p = -1) {↵
visited[v] = 1;↵
tin[v] = low[v] =timer++;↵
int children = 0;↵
↵
for (auto u:adj[v]) {↵
if (u == p) continue;↵
if (visited[u]) {↵
if (done[u][v] == 0) {↵
adj2[u].pb(v);↵
adj2[v].pb(u);↵
done[u][v] = 1;↵
done[v][u] = 1;↵
}↵
low[v] = min(tin[u],low[v]);↵
}↵
else {↵
dfs(u,v);↵
low[v] = min(low[u],low[v]);↵
↵
if (low[u] >= tin[v] and p != -1) {↵
is_cut[v] = 1;↵
}↵
if (low[u] > tin[v]) {↵
bridges++;↵
} else {↵
if (done[u][v] == 0) {↵
adj2[u].pb(v);↵
adj2[v].pb(u);↵
done[u][v] = 1;↵
done[v][u] = 1;↵
}↵
}↵
↵
++children;↵
}↵
}↵
↵
if (p == -1 and children > 1) {↵
is_cut[v] = 1;↵
}↵
}↵
↵
void dfs2(int cur,int par = -1) {↵
if (is_cut[cur] == 1 and cut_count == 0){↵
cut_count++;↵
return;↵
}↵
visited[cur] = 1;↵
for (auto u:adj2[cur]) {↵
if (u == par) continue;↵
if (visited[u] == 1) {↵
if (done[u][cur] == 0) {↵
cur_comp++;↵
done[u][cur] = 1;↵
done[cur][u] = 1;↵
}↵
}↵
else {↵
dfs2(u,cur);↵
if (done[u][cur] == 0) {↵
cur_comp++;↵
done[u][cur] = 1;↵
done[cur][u] = 1;↵
}↵
}↵
}↵
}↵
↵
void solve(){↵
↵
cin >> n >> m;↵
init();↵
for (int i = 0; i < m; ++i) {↵
int p,q;↵
cin >> p >> q;↵
adj[p].pb(q);↵
adj[q].pb(p);↵
}↵
↵
dfs(1);↵
↵
visited.clear();↵
visited.assign(n+1,0);↵
done.assign(n+1,vector<bool>(n+1,0));↵
for (int i = 1; i <= n; ++i) {↵
if (visited[i] == 0 and is_cut[i] == 0) {↵
cut_count = 0;↵
cur_comp = 0;↵
dfs2(i);↵
mx_comp = max(cur_comp,mx_comp);↵
if(cur_comp != 0) comp++;↵
} ↵
}↵
↵
for (int i = 1; i <= n; ++i) {↵
if (is_cut[i]) cnt_cric++;↵
}↵
↵
int p = max(1LL,comp + bridges);↵
int q = max(1LL,mx_comp);↵
int g = __gcd(p,q);↵
p /= g;↵
q /= g;↵
cout << cnt_cric << " " << bridges << " " << p << " " << q << "\n";↵
}↵
↵
↵
signed main(){↵
fast;↵
int test = 1;↵
cin>>test;↵
int i=1;↵
while(test--){↵
solve();↵
}↵
}↵
↵
↵
↵
~~~~~↵
↵
↵
</spoiler>↵
↵
↵
In this problem, we are given a connected graph G and the following terminologies are defined:-↵
↵
1. Critical node: a node in G whose removal disconnects G.↵
↵
2. Critical link: an edge in G whose removal disconnects G.↵
↵
3. Critical component: a maximal set of edges in G such that any two edges in the set lie on a common cycle (A cycle is a set of nodes ⟨v0, v1, . . . , v k−1 ⟩, where k ≥ 4, such that any two consecutive vi−1 and vi for 1 ≤ i ≤ k − 1 have an edge, v0 = vk−1 and vi for 0 ≤ i ≤ k −2 are all distinct).↵
↵
4. Largest critical component: a critical component with the maximum number of edges.↵
↵
We have to find number of critical nodes and critical links, p and q, where p/q is in an irreducible form and are defined as follows :-↵
↵
- p is the number of critical components↵
↵
- q is the number of edges in the largest critical component.↵
↵
Our approach to this problem is :↵
↵
find all the bridges and cut vertices first, remove all the bridges. now apply dfs through individual component and count the edges in that component, we divided this into two cases from here:-↵
↵
1. there a single cut vertex in the component remove it and count both components (components separated by cut vertex) as different↵
2. else take the complete component as a single critical component↵
↵
p will be the number of components counted with this dfs + bridges and q will be max edges in a component.↵
↵
But, this approach should fail, when the graph looks like this, however it passed all tests, can anyone help with this?↵
↵
↵
<spoiler summary="Expected Output">↵
2 0 3 4↵
</spoiler>↵
↵
<spoiler summary="Our Output">↵
2 0 1 12↵
</spoiler>↵
↵
<spoiler summary="Our Implementation">↵
↵
~~~~~↵
#include<bits/stdc++.h>↵
#define pb push_back↵
#define fast ios_base::sync_with_stdio(false); cin.tie(0); cout.tie(0)↵
#define ll long long↵
#define pii pair<int,int>↵
#define pll pair<ll,ll>↵
#define f first↵
#define s second↵
#define int long long↵
#define sz(x) (ll)(x.size())↵
using namespace std;↵
↵
↵
const int mod = 1e9+7;↵
↵
int expo_pow(int x,int y){↵
if(y == 0) return 1;↵
y=y%(mod-1);↵
x%=mod;↵
if(y==0) y=mod-1;↵
int res=1;↵
while(y){↵
if(y&1) res=(res*x)%mod;↵
x=(x*x)%mod;↵
y>>=1; ↵
}↵
return res;↵
}↵
↵
ll add()↵
{↵
return 0;↵
}↵
↵
template <typename T, typename... Types>↵
T add(T var1, Types... var2){↵
return (((((ll)(var1)) % mod + (ll)(add(var2...))) % mod) + mod) % mod;↵
}↵
↵
ll mul(){↵
return 1;↵
}↵
↵
template <typename T, typename... Types>↵
T mul(T var1, Types... var2){↵
return (((ll)(var1)) % mod * (ll)(mul(var2...))) % mod;↵
}↵
↵
int n,m;↵
vector<vector<int>> adj;↵
int cnt_cric,bridges;↵
vector<vector<int>> adj2;↵
vector<bool> visited;↵
vector<int> tin,low;↵
vector<bool> is_cut;↵
int timer,comp,mx_comp;↵
int cur_comp;↵
int cut_count = 0;↵
vector<vector<bool>> done;↵
↵
void init() {↵
adj.clear();↵
adj.resize(n+1);↵
adj2.clear();↵
adj2.resize(n+1);↵
tin.clear();↵
tin.resize(n+1);↵
low.clear();↵
low.resize(n+1);↵
visited.clear();↵
visited.assign(n+1,0);↵
is_cut.clear();↵
is_cut.assign(n+1,0);↵
done.clear();↵
done.assign(n+1,vector<bool>(n+1,0));↵
cnt_cric = 0;↵
bridges = 0;↵
timer = 0;↵
comp = 0;↵
mx_comp = 0;↵
}↵
↵
void dfs(int v,int p = -1) {↵
visited[v] = 1;↵
tin[v] = low[v] =timer++;↵
int children = 0;↵
↵
for (auto u:adj[v]) {↵
if (u == p) continue;↵
if (visited[u]) {↵
if (done[u][v] == 0) {↵
adj2[u].pb(v);↵
adj2[v].pb(u);↵
done[u][v] = 1;↵
done[v][u] = 1;↵
}↵
low[v] = min(tin[u],low[v]);↵
}↵
else {↵
dfs(u,v);↵
low[v] = min(low[u],low[v]);↵
↵
if (low[u] >= tin[v] and p != -1) {↵
is_cut[v] = 1;↵
}↵
if (low[u] > tin[v]) {↵
bridges++;↵
} else {↵
if (done[u][v] == 0) {↵
adj2[u].pb(v);↵
adj2[v].pb(u);↵
done[u][v] = 1;↵
done[v][u] = 1;↵
}↵
}↵
↵
++children;↵
}↵
}↵
↵
if (p == -1 and children > 1) {↵
is_cut[v] = 1;↵
}↵
}↵
↵
void dfs2(int cur,int par = -1) {↵
if (is_cut[cur] == 1 and cut_count == 0){↵
cut_count++;↵
return;↵
}↵
visited[cur] = 1;↵
for (auto u:adj2[cur]) {↵
if (u == par) continue;↵
if (visited[u] == 1) {↵
if (done[u][cur] == 0) {↵
cur_comp++;↵
done[u][cur] = 1;↵
done[cur][u] = 1;↵
}↵
}↵
else {↵
dfs2(u,cur);↵
if (done[u][cur] == 0) {↵
cur_comp++;↵
done[u][cur] = 1;↵
done[cur][u] = 1;↵
}↵
}↵
}↵
}↵
↵
void solve(){↵
↵
cin >> n >> m;↵
init();↵
for (int i = 0; i < m; ++i) {↵
int p,q;↵
cin >> p >> q;↵
adj[p].pb(q);↵
adj[q].pb(p);↵
}↵
↵
dfs(1);↵
↵
visited.clear();↵
visited.assign(n+1,0);↵
done.assign(n+1,vector<bool>(n+1,0));↵
for (int i = 1; i <= n; ++i) {↵
if (visited[i] == 0 and is_cut[i] == 0) {↵
cut_count = 0;↵
cur_comp = 0;↵
dfs2(i);↵
mx_comp = max(cur_comp,mx_comp);↵
if(cur_comp != 0) comp++;↵
} ↵
}↵
↵
for (int i = 1; i <= n; ++i) {↵
if (is_cut[i]) cnt_cric++;↵
}↵
↵
int p = max(1LL,comp + bridges);↵
int q = max(1LL,mx_comp);↵
int g = __gcd(p,q);↵
p /= g;↵
q /= g;↵
cout << cnt_cric << " " << bridges << " " << p << " " << q << "\n";↵
}↵
↵
↵
signed main(){↵
fast;↵
int test = 1;↵
cin>>test;↵
int i=1;↵
while(test--){↵
solve();↵
}↵
}↵
↵
↵
↵
~~~~~↵
↵
↵
</spoiler>↵
↵





