Warning: The following contains graphic depictions of geometry, precision errors, and degenerate cases. Viewer discretion is advised.
Prerequisites
I assume the reader is familiar with:
- 2D Convex Hulls
- 3D Vector Operations (dot and cross products)
Introduction
Recall that in the 2D convex hull problem, you are given a set of 2D points, and you must compute the smallest convex polygon containing all the given points. By convex, we mean that for any two points $$$A$$$ and $$$B$$$ inside the polygon, the entire line segment $$$AB$$$ is also inside the polygon.
The problem in 3D is completely analogous. You are given $$$n$$$ 3D points, and you must compute the smallest convex polyhedron containing all the given points. Similarly, a polyhedron is convex if for any two points $$$A$$$ and $$$B$$$ inside the polyhedron, the line segment $$$AB$$$ is also inside the polyhedron.
In the 2D case, it is more obvious what the output is. We can simply output a circular list of vertices on the boundary of the polygon. But how do we represent a polyhedron? Well, we can represent it as a list of triangular faces. A non-triangular face can always be divided into triangles, so this requirement isn't limiting.
In the 2D case, there are some degenerate cases that are easy to miss if you're not careful. For example, if there are 3 collinear points, the polygon might have two adjacent sides of the same slope, or you might combine them into one segment. Or if two points have the same $$$x$$$ coordinate, you need to handle this carefully when sorting the points by $$$x$$$ coordinate. Or if all the points are on the same line, then the convex hull isn't even a non-degenerate polygon!
Now, degenerate cases are bad enough with two dimensions. When you enter the third dimension, it only gets worse. What if four points lie on the same plane? Since we are requiring triangular faces, we could triangulate this in multiple ways. Or maybe we could choose to have one triangle of three points and the forth point lies inside this triangle, so we ignore it. What if all the points are on the same line? Or on the same plane even? Then the convex hull isn't a non-degenerate polyhedron. I will ignore such degenerate cases for now, and revisit them when applicable.
Brute Force Algorithm in $$$O(n^4)$$$
Suppose that $$$n$$$ is very small, and we are guaranteed that no four points are coplanar. Then how can we compute the 3D convex hull in the dumbest way possible?
We could simply consider every triplet of three points $$$(\vec{a}, \vec{b}, \vec{c})$$$, and check if they create a triangular face on the convex hull. In order for it to be a face, the remaining points must "see" the same side of the triangle. In other words, if we consider the plane containing this triangle, the remaining points should lie on the same side of the plane. To compute which side of a plane a point $$$\vec{p}$$$ is on, we can first take a vector $$$\vec{q}=(\vec{b}-\vec{a})\times (\vec{c}-\vec{a})$$$ orthogonal to the plane.
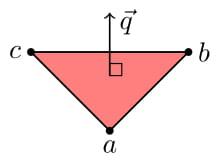
Then the sign of $$$(\vec{p}-\vec{a})\cdot \vec{q}$$$ tells us the side of the plane. In particular, a result of $$$0$$$ tells us that $$$\vec{p}$$$ lies on the plane.
For each triplet, we perform this check with all points, so the total time complexity is $$$O(n^4)$$$. Because of its simplicity, this should be the approach when the constraints allow it. And by examining the brute force case, we learned how to perform the most fundamental operation in any 3D convex hull algorithm: checking which side of a plane a point is on.
Incremental Algorithm in $$$O(n^2)$$$
Now we want a more practical algorithm. The strategy of the incremental algorithm is to build the convex hull for the first $$$i$$$ points, as $$$i$$$ goes from $$$1$$$ to $$$n$$$. All we have to do is figure out how to update the convex hull in order to accommodate one new point.
Let's start by making an analogy with the 2D convex hull. Suppose we currently have the convex hull of the first $$$i-1$$$ points, and we wish to add the $$$i$$$-th point. Well, if the point is already inside the hull, we should do nothing. Otherwise, let's pretend we are looking at the polygon from the perspective of the $$$i$$$-th point. We should delete all line segments it can see, and add two new line segments: one from the new point to each of the extreme points.
A similar thing happens in the 3D case. If a point is already inside the polyhedron, we simply do nothing. Otherwise, we delete all faces the new point can see. But what's less obvious is what we should add. Well, we've left the polyhedron with a connected set of faces removed. This exposes a cycle of edges. For each of these exposed edges, we should create a new face with the new point and that edge. Effectively, we create a cone of faces to repair the open face.





