Hi everyone!

Let's continue with learning continued fractions. We began with studying the case of finite continued fractions and now it's time to work a bit with an infinite case. It turns out that while rational numbers have unique representation as a finite continued fraction, any irrational number has unique representation as an infinite continued fraction.

Distance between convergents. In the first part we learned that for continued fraction $$$r=[a_0, a_1, \dots, a_n]$$$ elements of the sequence $$$r_0, r_1, \dots, r_n$$$ where $$$r_k = [a_0, a_1, \dots, a_k]$$$ are called convergents. We also derived that subsequent convergents obey a simple formula:

Subsequent convergents seemingly should be closer to $$$r$$$ with bigger $$$k$$$, culminating in $$$r_n=r$$$. So, let's find some bound on how far away from $$$r$$$ can $$$r_k$$$ be. We may start with looking on the difference between $$$r_k$$$ and $$$r_{k-1}$$$:

Let's rewrite the numerator of this fraction:

Which means that numerator of $$$r_k - r_{k-1}$$$ is the opposite of numerator of $$$r_{k-1} - r_{k-2}$$$. The base case here is defined by $$$p_0 q_{-1} - p_{-1} q_0$$$, which is equal to $$$-1$$$. In this way we may conclude that $$$p_k q_{k-1} - p_{k-1} q_k = (-1)^{k-1}$$$, thus the whole difference is written as follows:

Further we will also need to know the distance between $$$r_{k+1}$$$ and $$$r_{k-1}$$$:

Approximation properties. Formulas above allow us to represent number $$$r=r_n$$$ as explicit telescopic sum (given that $$$r_0=a_0$$$):

Since $$$q_k$$$ monotonically increases, we may say that $$$q_{k+1} q_k > q_k q_{k-1}$$$, thus we have an alternating sum which terms are decreasing by absolute value. This fact automatically implies several important properties, which may be illustrated by the picture below:

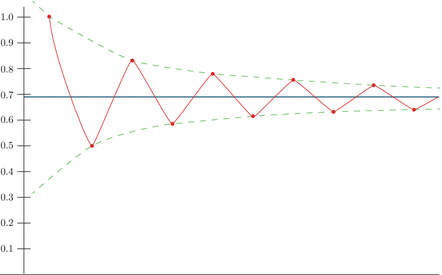
In our specific case difference between subsequent convergents quickly drops:

Consequent convergents maintain lower and upper bound on possible values of $$$r$$$ and each summand makes one of bounds more accurate. Bound above means that segment of possible $$$r$$$ is at least halved on each step. Few important corollaries from this:

• Convergents with even indices are lower than $$$r$$$ while convergents with odd indices are greater than $$$r$$$,
• If indices $$$j$$$ and $$$i$$$ have different parity then:

• If indices $$$j$$$ and $$$i$$$ have same parity and $$$j>i$$$ then:

• If $$$j>i$$$, then $$$|r_i - r| \geq |r_j - r|$$$.

These observations provide us convenient means of estimating how close is $$$r_k$$$ to $$$r$$$:

So, the final "pretty" bounds on the distance between $$$r_k$$$ and $$$r$$$ may be written as follows:

Geometric interpretation. Consider sequence $$$s_k = (q_k;p_k)$$$ on 2-dimensional space. Each point $$$s_k$$$ corresponds to convergent $$$\frac{p_k}{q_k}$$$ which is the slope coefficient of the vector from $$$(0;0)$$$ to $$$(q_k;p_k)$$$. As was mentioned earlier, convergent coefficients are determined by formula:

Geometrically it means that $$$s_k=a_k s_{k-1} + s_{k-2}$$$. Let's recall how coefficients $$$a_k$$$ are obtained. Let $$$b_0, b_1, \dots, b_n$$$ be the states of $$$r$$$ at each step. Thus, we initially have $$$b_0=r$$$ and then for each $$$b_k$$$ we calculate $$$a_k = \lfloor b_k \rfloor$$$ and say that $$$b_{k+1} = \frac{1}{b_k - a_k}$$$. So, for example:

If you look closely, you may see that numerator of $$$b_k$$$ is the denominator of $$$b_{k-1}$$$ and denominator of $$$b_k$$$ is given by:

Thus, the whole number $$$b_k$$$ may be defined as follows:

Delaunay.