[Russian version is in progress now, will be published ASAP]

Hello, CodeForces.

I think that matroids are beautiful and powerful concept, however, not really well known in competitive programming.

I’ve discovered matroids at 2019 Petrozavodsk Winter Training Camp. There was a problem that clearly cannot be solved using usual techniques I knew, editorial for this problem was just these three words “just matroid intersection”. Back then it took me more than 2 days of upsolving to find all the information and details I need and implement solution that gets AC on this. And it took way longer to actually understand why does it work and exactly how does it work. (I still hesitate in some details.)

Of course, it is not hard to google up all the definitions and some related articles, but in my opinion they all are focused more on mathematical part of theory, strict proofs in some not really obvious but short ways, and observing only key points in whole theory, omitting a lot of intermediate results, logical steps and examples. In some article I’ve encountered this heavy-formula proof:

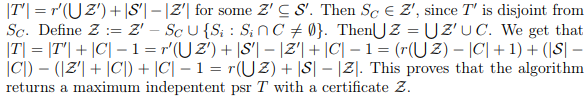
That was nowhere close to being clear for me. (Probably I’m not mathematician enough, yet.) But still, I’m sure there is a way to make this more clear and detailed.

I am sure, there are a lot of people in CP who will also like to get familiar with matroids. So, I’ve decided to review this topic from very beginning focusing more on explanations, logical steps and providing more examples. This is the goal of this article, and you do not need to know anything about matroids beforehand. .

Prerequisites. You are not required to know well everything listed here, but it is good to be familiar with some of these concepts for better and faster understanding:

1. Basics of set theory and set operations
2. Spanning trees in graphs
3. Matchings in bipartite graphs
4. Linear independence in vector spaces
5. Rank and basis of set of vectors
6. Gaussian elimination
7. Kruskal’s minimum spanning tree algorithm
8. Kuhn’s bipartite matching algorithm
9. Enjoying discrete math

All the information that used in this article is my own understanding of this topic, that I’ve learned from other articles found on the web. And as we know, proof by passing various tests is not a proper proof. So if you find something illogical or wrong, that should mean that I’ve made a mistake or misinterpret something, please point it out.

What matroid is?

Matroid is a structure that abstracts and generalizes the notion of linear independence in vector spaces.

Here goes the formal definition. Matroid is a pair $$$\left\langle X, I \right\rangle$$$ where $$$X$$$ is called ground set and $$$I$$$ is set of all independent subsets of $$$X$$$. In other words matroid $$$\left\langle X, I \right\rangle$$$ gives a classification for each subset of $$$X$$$ to be either independent or dependent (included in $$$I$$$ or not included in $$$I$$$).

Of course, we are not speaking about arbitrary classifications. These $$$3$$$ properties must hold for any matroid:

1. Empty set is independent.
2. Any subset of independent set is independent.
3. If independent set $$$A$$$ has smaller size than independent set $$$B$$$, there exist at least one element in $$$B$$$ that can be added into $$$A$$$ without loss of independency.

These are axiomatic properties of matroid. To prove that we are dealing with matroid, we generally have to prove these three properties.

For example, explicit presentation of matroid on ground set $$$\{x, y, z\}$$$ which considers $$$\{y, z\}$$$ and $$$\{x, y, x\}$$$ to be dependent and marked red. Other sets are independent and marked green.

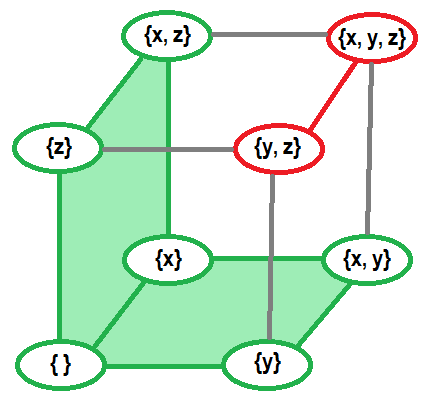
From this definition we can derive some other important concepts (examples for all these concepts will be shown later, along with examples of matroids):

Bases. Any independent set of maximum size is a basis of given matroid. In other words there is not element that can be added to a basis without loss of independency. All bases have equal size (otherwise we can add something to smaller basis from greater basis by third axiomatic property). Directly from previous, no basis is a subset of other basis. Any independent set is a subset of some basis (by third property we can continue increasing its size until reaching some basis), so it is enough to only know about all bases of matroid to completely describe it.

Circuits. Dependent set is a circuit if all subsets (excluding whole set) of this set are independent. In other words, circuit is dependent set, that does not allow removing any of its elements without gaining independence. No circuit is a subset of another circuit (otherwise we can remove some elements from greater circuit without removing dependence).

Another important property of circuits, symmetric difference of two different circuits always contain a circuit. Symmetric difference of two sets contains all elements that are included only in one of the sets (formally, $$$A \Delta B = (A \setminus B) \cup (B \setminus A)$$$). This property is related to cycle spaces, in case of matroids this can be generalized to “circuit spaces”.

Ranks. Ranking function. Rank of matroid is size of its bases. But we can directly refer it as size of the basis, why would we need specific definition for such thing? Yes, this is not really a flexible thing (we can refer it as size of basis), to make it more flexible we can define ranking function $$$r(S)$$$ that tells maximum size of independent subset for some $$$S$$$, which is subset of ground set. Value of ranking function on some subset can be referred as rank of this subset in matroid. This information about subsets can be very helpful in many situations. Some properties of ranking functions:

1. Rank of subset cannot be greater than size of this subset.
2. Rank of independent subset is size of this subset.
3. Rank of whole ground set is equal to rank of matroid. Rank of empty set is $$$0$$$.
4. Rank of any subset of set $$$S$$$ is not greater than rank of $$$S$$$.
5. Including $$$1$$$ element into set can only increase its rank by $$$1$$$ or leave it unchanged. (formally, for some set $$$S$$$ and element $$$x \notin S$$$ we have $$$r(S) \leq r(S \cup \{x\}) \leq r(S)+1$$$)
6. Ranking function of matroid is submodular. If we have two sets $$$A$$$ and $$$B$$$, moving all elements that are present in $$$B$$$ but not present in $$$A$$$ from $$$B$$$ to $$$A$$$ will not improve sum of ranks of both sets. Formally, $$$r(A) + r(B) \geq r(A \cup B) + r(A \cap B)$$$. In general element will not contribute more to a rank if it is moved to a set with additional elements. This might get more clear if explicitly split $$$A$$$ and $$$B$$$ into $$$A’ = A \setminus B$$$, $$$C’ = A \cap B$$$ and $$$B’ = B \setminus A$$$ and write it in a form $$$r(A’ \cup C’) + r(B’ \cup C’) \geq r(A’ \cup B’ \cup C’) + r(C’)$$$. See pictures below for example:

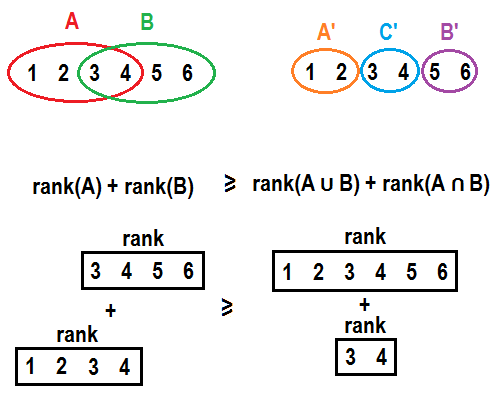
Speaking informally, principle “it is better not to puts many eggs into one basket” works here.

Independence oracle. Speaking about classifications of subsets, we usually cannot afford storing it as some information about each subset (it will result in exponential memory consumption). We need some other tools to test subsets for independence. If matroid is defined as a consequence of relations among elements in some other structure, we usually (probably, always?) can find algorithm with polynomial running time to test some subset of elements for independence. As we would like to abstract concept of matroids and use them regardless of their underlying independence mechanism, we can define independence oracle as subroutine that tests some subset for independence. And we can measure running time of some algorithms as the number of oracle calls. (However, in practice we cannot completely forget about this, because we will miss great opportunities to optimize related algorithms.)

Examples

There are matroids of different types. There are some examples:

Uniform matroid. Matroid that considers subset $$$S$$$ independent if size of $$$S$$$ is not greater than some constant $$$k$$$ ($$$|S| \leq k$$$). Simplest one, this matroid does not really distinguish elements of ground set in any form, it only cares about number of taken elements. All subsets of size $$$k$$$ are bases for this matroid, all subsets of size $$$(k+1)$$$ are circuits for this matroid. We can also define some specific cases of uniform matroid:

1. Trivial matroid. $$$k = 0$$$. Only empty set is considered independent, any element of ground set is considered dependent (any combination of ground set elements is also considered dependent as a consequence).
2. Complete matroid. $$$k = |X|$$$. All subsets are considered independent including complete ground set itself.