I decided to write this blog, as a lot of people were requesting for the editorial of Shortest Path Constrained problem from CodeNation Hiring Test, held on 26th January, 2019

Problem

Statement

There is a weighted undirected graph with N nodes and M edges. You are also given X different sets of nodes — S₁ to S_x. You have to give the shortest possible distance between a start node — a and a destination node — b, along a path following the following rule: For all i < j, before visiting a node in S_j, you must visit all the nodes in S_i.

The distance is defined as sum of weights of edges along the path traversed.

Note :-

1. The path must contain all the nodes in union of S_i for all 1 ≤ i ≤ X
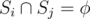2. for all 1 ≤ i, j ≤ X and i ≠ j.
3. The path may go through any node, including a and b, more than once. The constraint is that it must end at b

Constraints

• 2 ≤ N ≤ 100
• 0 ≤ w ≤ 100000
• 0 ≤ X ≤ 10
• 1 ≤ |Si| ≤ 10 for all i ≤ X
• Nodes are numbered from 0 to N - 1
• The graph does not contains multiple edges or self edges, and is connected

Solution

Let us first solve the problem of how to visit all the nodes in a set S_i, in shortest possible distance, such that we end up at node x. This problem can be solved using dp + bitmask. Suppose dp[bitmask][x] stores the minimum distance, for this particular set, such that the nodes with bits set to 1 in bitmask are visited, and we end up at node x. Now for all k such that k^th bit is 0 in bitmask, we can update dp[bitmask|k][k] = min(dp[bitmask][x] + dist(x, k), dp[bitmask|k][k])