I want to discuss a type of data structure that I (personally) haven't really seen get any attention. It doesn't really do anything special, but I still find it interesting enough that it should be at least noticed.

It is an alternative to Fenwick trees (aka binary indexed trees), in the sense that it solves the same class of problems, in a memory-efficient way (unlike segment trees or binary search trees). Although the implementation has a couple extra lines of code, (in my subjective opinion at least,) it is easier to visualize and understand conceptually when compared to Fenwick trees. In fact, my motivation for writing this is that personally I've had a hard time learning BITs and understanding them (beyond memorizing the code) and for a long time I've avoided them in favor of segment trees or (when time/memory restrictions were tight), a structure similar to the one I'll be describing.

With that out of the way, the sample problem we are trying to solve is the following: given an sequence of N numbers, execute two kinds of queries: update (increase the value at some index by some value) and query (print the sum of all numbers up to some position).

We are going to build a binary tree in which node #i holds the sum of numbers in some range centered in i. How would we build this kind of tree (conceptually) from a given sequence of numbers?

1. we want to build a tree which covers the indexes in interval [l,r) -- initially, [0,N)
2. recursively build the tree which covers [l,mid) and set it as this node's left son
3. recursively build the tree which covers [mid+1,r) and set it as this node's right son
4. the value in this node is the sum of the values in its children plus sequence[mid]

Here's a visualization of what this tree looks like for the sequence (of length 6) {1, 10, 100, 1000, 10000, 100000}:

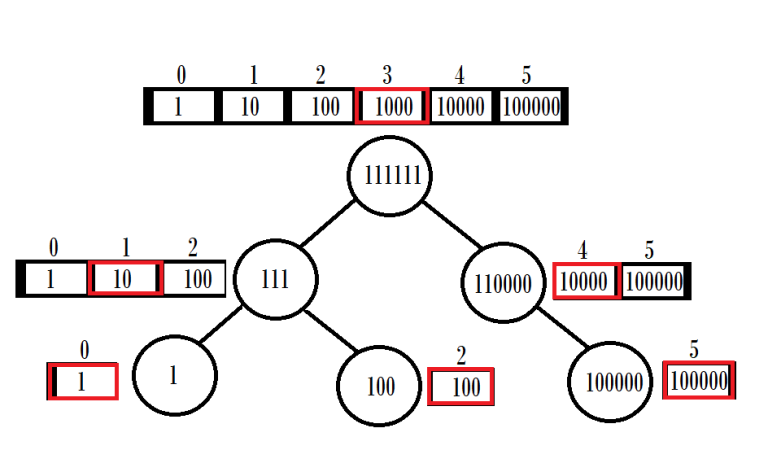
It is easy to see that such a tree has exactly N nodes and a height of ceil(log2(N)). The nice thing about this construction is that we can always represent it as an array of numbers of length N, in which the ith element corresponds to the value inside the node which holds a range centered in i. We also don't need to keep any pointers to the left and right nodes, since we can compute them on the fly.

Now let's get to solving the problem at hand.

How do you perform an update operation (i.e. increasing the value at some index by some value)? We start at the top node (which contains the entire array). When we get to a node, add the update value to this node's value. Then, if the update index is smaller than this node's index, we need to go to the left subtree. If the update index is greater, go to the right subtree. Otherwise, (if the indexes are equal), we can stop. Keep in mind that "this node's index" is given by the average of the left and right of the node's range. Sample code for this operation:

void update(int pos, int x) {
  for (int l = 0, r = N; l < r;) {
    int mid = (l + r) / 2;
    tree[mid] += x;
    if (mid == pos) return;
    if (pos < mid) r = mid;
    else l = mid + 1;
  }
}

What about querying (i.e. asking "what is the sum up to a given position")? Again, start from the top. If the queried position is less than the current node's index, move the query to the left subtree. Otherwise, move to the right subtree, but we have to add all of the elements to the left and inside the current node. In other words, if current node is represented by range [l,r), when we make the leap to node [mid+1,r) (the right subtree), we have to add all elements inside range [l,mid]. We don't have this value explicitly (left node holds interval [l,mid), not [l,mid]), but we can obtain it by noticing that the sum [l,mid] is the sum [l,r) minus the sum [mid+1,r]. In other words, it is the value inside the current node minus the value inside the right subtree. Sample code for this operation:

int query(int pos) {
  int ans = 0;
  for (int l = 0, r = N; l < r;) {
    int mid = (l + r) / 2;
    if (pos < mid) r = mid;
    else {
      ans += tree[mid];
      l = mid + 1;
      if (l < r) ans -= tree[(l + r) / 2];
    }
  }
  return ans;
}

You can make various modifications to this structure. For example, you can implement single-pass range queries (currently, if you want to know the sum from an interval, you have to take the difference of two queries), which in offers better performance (even when compared to Fenwick trees, in my experience). You can also easily implement range updates with lazy propagation (the same way you would do it for a segment tree).

For sample problems, any problem which uses Fenwick trees will work, really. This is an educational problem for learning Fenwick trees. The memory limit is low to prevent segment tree solutions. The page is in Romanian but google translate works wonders.