Problem A – Academia
ENGLISH
PORTUGUESE
Esta é uma questão de programação dinâmica e/ou simulação. Ela é uma derivada do clássico Problema da Mochila.
Primeiro faremos um vetor, de tamanho de 0 até Tmax (Tmax + 1), onde simularemos o "quão pesada está nossa mochila", ou seja, o quanto tempo gastamos.
Inicialmente o vetor estará preenchido com zeros, pois não teremos nenhum Poder de Musculação.
Para cada exercício faremos as seguintes ações:
1) Iremos ver o vetor entre [0, Tmax - Texercício], esse vetor é nosso armazenamento para cada teste.
2) Para ti entre [0, Tmax - Texercício] iremos propagar a soma do Poder de Musculação do vetor[ti] e o Pexercício para o próximo tempo.
3) Faremos então:
vetor[ti + Texercício] = maior(vetor[ti] + Pexercício, vetor[ti + Texercício])
OBS: Fazer ti entre [0, Tmax - Texercício] ir da direita para esquerda para não haver sobreposição de Poder de Musculação
No final procurar o maior valor de P no vetor e imprimir.
Tempo: O(Tmax * n).
Problem B – Bento
ENGLISH
It is a brute force question. It is not given the size of the rectangular room, so it can be any value. The principle question is you analyze if is possible to make something rectangular with a number N of tiles, independently of the room size.
Than the number of tiles will be the number of tiles in colummn multiplied by the number of tiles in row.
For example, 8 tiles -> you can use 2 for column and 4 for row, and vice-versa, being: 2 * 4 = 8.
So we want to know if L * C = N, but L and C cant be 1, so N have to be multiple of L and C.
For that, if N is prime than it cant done, otherwise it can be done.
Since the maximum size of N is 1012 it is needed to make a faster method to analyze divisors of N, verifying from 1 to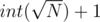 
, if some of it in this interval divide N, than it is not prime, otherwise it is prime.
The worst case of N is 1012, than we do up to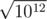 
maximum, that is equals to 106.
Another observation, 1012 overflows the size of integer in C/C++/JAVA, for that we use 'unsigned long long int' for C/C++ or 'BigInteger' for Java. Outra observação, 1012 estoura o tamanho de inteiro em C/C++/JAVA, por isso em C/C++ use 'unsigned long long int' ou 'BigInteger' no Java.
Time: 
PORTUGUESE
É uma questão de força bruta. Não é dado o tamanho da sala retangular, então pode ser de qualquer valor. O princípio da questão é você analisar se, independentemente do tamanho da sala, é possível fazer algo retangular com o número N de azulejos.
Então o número de azulejos vai ser o número de azulejos "em coluna" vezes o número de azulejos "em linha".
Por exemplo, 8 azulejos -> você pode usar 2 pra coluna e 4 pra linha, e vice-versa, ficando: 2 * 4 = 8.
Então queremos saber se L * C = N, porém L e C não podem ser 1, logo N tem que ser Múltiplo de L e C.
Para isso, se N é primo então não dá pra fazer, se N não é primo então dá pra fazer.
Como o tamanho máximo de N é 1012 é preciso fazer o método rápido para analisar os divisores de N, verificando de 1 até 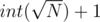, se algum desses neste intervalo divide N, então não é primo, caso contrário é primo.
Então para o pior caso de N ser 1012, faremos até 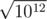que é igual a 106.
Outra observação, 1012 estoura o tamanho de inteiro em C/C++/JAVA, por isso em C/C++ use unsigned long long int ou BigInteger no Java.
Tempo:
Problem C – Codex
ENGLISH
PORTUGUESE
É uma questão com duas soluções viáveis uma com implementação com técnica de programação (Busca Binária) ou implementação com Map/Hash. Explicaremos a forma mais fácil.
Criaremos dois Maps (Um para dado o índice ter o elemento e outro para dado o elemento ter o índice):
MapM, M[índice] = elemento.
MapV, V[elemento] = índice.
Iremos manipular os dois.
Para operação 1:
índice = V[elemento]
Unable to parse markup [type=CF_TEX]
índicepróximo = V[próximo]
V[elemento] = índicepróximo
V[próximo] = índice
M[índice] = próximo
M[índicepróximo] = elemento
A partir daí teremos trocas em tempo O(logn).
Para a operação teremos - 1 será análogo, porém para o anterior, lembrando do caso do elemento ser o menor e trocar com o maior.
Para imprimir o resultamos, faremos um laço de i indo de 0 até n - 1 imprimindo M[i].
Problem D – Dijkstra
ENGLISH
PORTUGUESE
É uma questão de Grafo utilizando o conhecimento de LCA (Lowest Common Ancestor — Menor Ancestral Comum). Qualquer solução ingênua é aceita desde que tenha a lógica de um LCA. Primeiro iremos enraizar o grafo a partir de um vértice qualquer.
Exemplo do caso 2, vamos enraizar em 1. Para enraizar podemos usar o algoritmo de Busca em Profundidade ou Largura, onde armazenaremos o pai e o nível do vértice i. Para o pai de 1 é -1 e o nível de 1 é 0, por padrão.
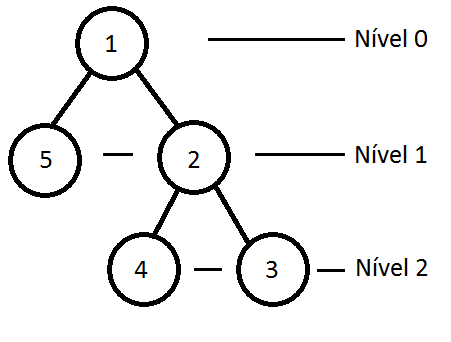
Agora para saber quem é o menor ancestral comum temos seguinte algoritmo.
Temos u e v que é o número do vértice. Vamos fazer com que o u seja o vértice de maior nível, e v é o vértice de menor nível.
Vamos subir o u para ficar no mesmo nível de v.
Enquanto nível[v] != nível[u] faça
u = pai[u]
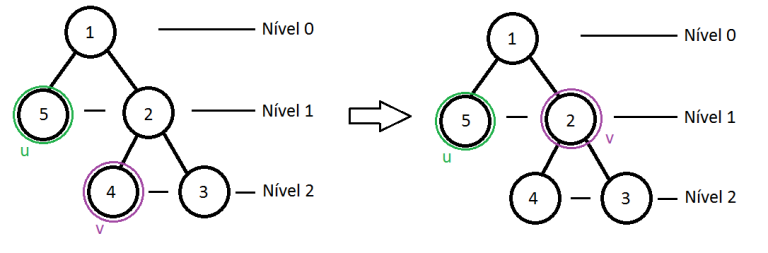
Após isso, você vai subir simultaneamente v e u até achar um vértice que seja comum e retornará ele.
Enquanto u != v faça
u = pai[u]
v = pai[v]
retorne u
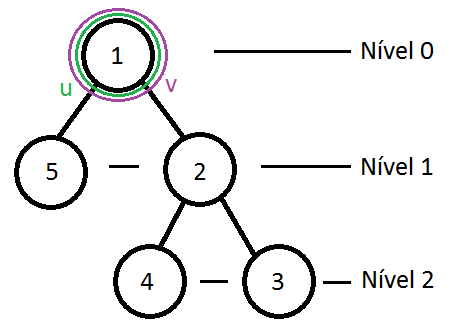
Tempo: O(n), pior caso, seja uma lista encadeada.
Problem E – Finding Paths
ENGLISH
PORTUGUESE
Problem F – Making life easier for Miguel
ENGLISH
It is a brute force question, with binary search if you like.
The binary number formed by 1's is a decimal number in the form 2k - 1.
For that we need to find a k that satisfy that condition, where 1018 ≤ 260, then we need just to make 60 iteracions to analyze.
The easyest and fastest method is to use a bit-to-bit operation. Doing the following: N&(N + 1), for example:
Than, if N&(N + 1) is equals to 0, than N is in 2k–1 form, otherwise no.
Time: Bit-to-Bit "O(1)", Analyze O(logk).
PORTUGUESE
É uma questão de força bruta, com otimização em busca binária se quiser.
O número em binário onde é formado só por 1's é um número decimal da forma 2k - 1.
Para isso só precisamos achar um k que satisfaça essa condição, onde 1018 ≤ 260, então precisaremos fazer 60 iterações de análise.
O método mais fácil e rápido é utilizar operação bit-a-bit. Fazemos o seguinte: N&(N + 1), por exemplo:
Então, se N&(N + 1) é igual a 0, então N é da forma 2k–1, caso contrário não.
Tempo: Bit-a-Bit "O(1)", Analise O(logk).
Problem G – Gaining Points
ENGLISH
PORTUGUESE
Problem H – Hiperspace
ENGLISH
It is a brute force/implementation question. We just have to make 3 verifications, if n ≤ 299 you show 'Hiperespaco nao esta disponivel', else if n ≤ 499 you show 'Hiperespaco esta disponivel', else you show 'Hiperespaco ativado'.
Time: O(1).
PORTUGUESE
É uma questão de força bruta/implementação. São apenas 3 verificações, se n ≤ 299 você imprime 'Hiperespaco nao esta disponivel', se não, se n ≤ 499, você imprime 'Hiperespaco esta disponivel', senão você imprime 'Hiperespaco ativado'.
Tempo: O(1).
