NOTE : Knowledge of Binary Indexed Trees is a prerequisite.
Problem Statement
Assume we need to solve the following problem. We have an array, A of length N with only non-negative values. We want to perform the following operations on this array:
Update value at a given position
Compute prefix sum of A upto i, i ≤ N
Search for a prefix sum (something like a
lower_boundin the prefix sums array of A)
Basic Solution
Seeing such a problem we might think of using a Binary Indexed Tree (BIT) and implementing a binary search for type 3 operation. Its easy to see that binary search is possible here because prefix sums array is monotonic (only non-negative values in A).
The only issue with this is that binary search in a BIT has time complexity of O(log2(N)) (other operations can be done in O(log(N))). Even though this is naive, here is how to do it:
Most of the times this would be fast enough (because of small constant of above technique). But if the time limit is very tight, we will need something faster. Also we must note that there are other techniques like segment trees, policy based data structures, treaps, etc. which can perform operation 3 in O(log(N)). But they are harder to implement and have a high constant factor associated with their time complexities due to which they might be even slower than O(log2(N)) of BIT.
Hence we need an efficient searching method in BIT itself.
Efficient Solution
We will make use of binary lifting to achieve O(log(N)) (well I actually do not know if this technique has a name but I am calling it binary lifting because the algorithm is similar to binary lifting in trees using sparse table).
What is binary lifting?
In binary lifting, a value is increased (or lifted) by powers of 2, starting with the highest possible power of 2, 2⌊ log(N)⌋, down to the lowest power, 20.
How binary lifting is used?
We are trying to find pos, which is the position of lower bound of v in prefix sums array, where v is the value we are searching for. So, we initialize pos = 0 and set each bit of pos, from most significant bit to least significant bit. Whenever a bit is set to 1, the value of pos increases (or lifts). While increasing or lifting pos, we make sure that prefix sum till pos should be less than v, for which we maintain the prefix sum and update it whenever we increase or lift pos. See implementation.
It is not very difficult to come up with a rigorous proof of correctness and I am leaving it as an exercise for the readers.
HINT : Each position in bit stores sum of a power of 2 elements, sum of last i& - i (this isolates least significant bit of i) elements till i are stored at position i in bit. I hope this will atleast help you think of an intuitive proof.
Implementation :
// This is equivalent to calculating lower_bound on prefix sums array
// LOGN = log(N)
int bit[N]; // BIT array
int bit_search(int v)
{
int sum = 0;
int pos = 0;
for(int i=LOGN; i>=0; i--)
{
if(pos + (1 << i) < N and sum + bit[pos + (1 << i)] < v)
{
sum += bit[pos + (1 << i)];
pos += (1 << i);
}
}
return pos + 1; // +1 because 'pos' will have position of largest value less than 'v'
}
Example
I am using the example from TopCoder BIT Tutorial, which I recommend you to take a look at if you haven't already (**very important** for understanding this).
Let this be array A,

The BIT for this array will look as follows,
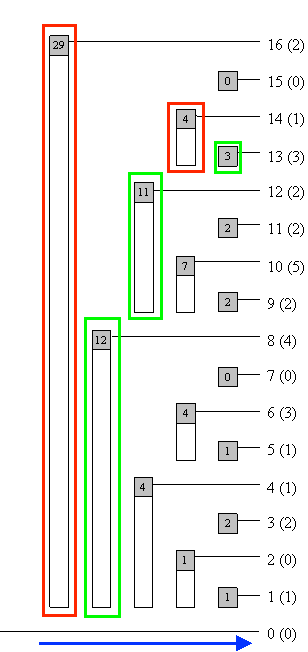
(Illustrations taken from https://www.topcoder.com/community/data-science/data-science-tutorials/binary-indexed-trees/)
Let us assume we want to search for v = 27. The blue arrow shows the direction in which we proceed in our search. Red shows that we can't lift pos. Green shows that we lift pos.
This is how the algorithm proceeds,
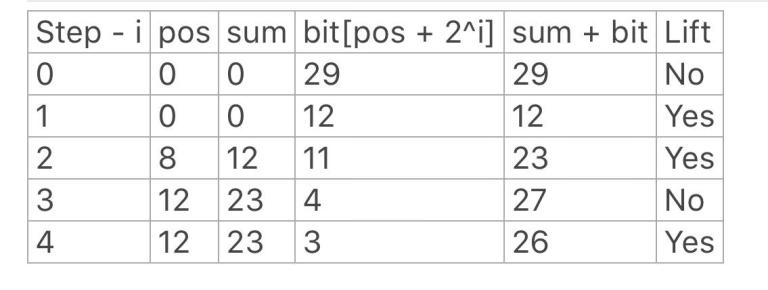
Finally, pos = 13, sum = 26 after last step.
Targetpos = pos + 1 = 14. You can verify that 14 is indeed the lower bound of 27 in prefix sums array!
I hope this helps in understanding the algorithm better. If it is still unclear go through TopCoder BIT Tutorial to understand the structure of BIT so that it can be related to this example.
Taking this forward
You must have noted that proof of correctness of this approach relies on the property of the prefix sums array that it monotonic. This means that this approach can be used for with any operation that maintains the monotonicity of the prefix array, like multiplication of positive numbers, etc.
Thats all folks!
PS : Please let me know if there are any mistakes.
UPDATE : As requested by some people, I have added an example for explain the algorithm.






