UPD: while I was translating this post from Russian to English, dacin21 wrote his post, more advanced, link. I hope that my post will help beginners, but in my post more rough estimates.
And in Russia we call rolling hashes as a polynomial hashes.
Hello, codeforces! This blogpost is written for all those who want to understand and use polynomial hashes and learn how to apply them in solving various problems. I will briefly write the theoretical material, consider the features of the implementation and consider some problems, among them:
Searching all occurrences of one string of length n in another string length m in O(n + m) time
Searching for the largest common substring of two strings of lengths n and m (n ≥ m) in O((n + m·log(n))·log(m)) time
Finding the lexicographically minimal cyclic shift of a string of length n in O(n·log(n)) time
Sorting of all cyclic shifts of a string of length n in lexicographic order in O(n·log(n)2) time
Finding the number of sub-palindromes of a string of length n in O(n·log(n)) time
The number of substrings of string of length n that are cyclic shifts of the another string length m in O((n + m)·log(n)) time
The number of suffixes of a string of length n, the infinite extension of which coincides with the infinite extension of the given string for O(n·log(n)) (extension is a duplicate string an infinite number of times).
Largest common prefix of two strings length n with swapping two chars in one of them O(n·log(n))
Note 1. It is possible that some problems can be solved more quickly by other methods, for example, sorting the cyclic shifts — this is exactly what happens when constructing a suffix array, to search for all occurrences of one string in another will allow the Knut-Morris-Pratt algorithm, the Manaker algorithm works well with the sub-palindromes, and for own suffixes there is a prefix function.
Note 2. In the problems above, an estimate is made when a hash search is performed by sorting and binary searching. If you have your own hash table with open mixing or overflow chains, then you — lucky, boldly replace the hash search for a search in your hash table, but do not try to use std::unordered_set, as in practice the search in std::unordered_set loses sorting and binary search in connection with the fact that this piece obeys the C++ standard and has to guarantee a lot to the user, which is useful for industrial coding and, often, is useless in the competitive programming, so sorting and binary search for simple structures gain absolute primacy in C++ in speed of work , if not used additional own structures.
Note 3. In cases where comparison of elements is slow (for example, comparison by hash in O(log(n)) time), in the worst case std::random_shuffle + std::sort always loses std::stable_sort, because std::stable_sort guarantees the minimum number of comparisons among all sorts (based on comparisons) for the worst case.
The solution of the listed tasks will be given below, the source codes also.
As advantages of polynomial hashing I can notice that you often do not need to think, you can immediately take and write a naive algorithm to solve the problem and speed it up with polynomial hashing. Personally, firstly, I think about solution with a polynomial hash, perhaps that's why I'm blue.
Among the disadvantages of polynomial hashing: a) Too many operations getting remainder from the integer division, sometimes on the border with TLE for large problems, and b) on the codeforces in C++ programs are often small guarantees against hacking due to MinGW: std::random_device generates the same number every time, std::chrono::high_resolution_clock ticks in microseconds instead of nanoseconds. (The Cygwin compiler for windows wins against MinGW).
What is polynomial hashing?
Hash-function must assign to the object a certain value (hash) and possess the following properties:
If two objects are equal, then their hashes are equal.
If two hashes are equal, then the objects are equal with a high probability.
A collision is the very unpleasant situation of equality of two hashes for not equal objects. Ideally, when you choose a hash function, you need to ensure that probability of collision lowest of possibles. In practice — just a probability to successfully pass a set of tests to the task.
Consider the sequence {a0, a1, ..., an - 1}. Under the polynomial hash for this sequence, we have in mind the result of calculating the following expression:
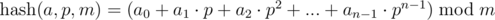
Here p and m — point (or base) and a hash module, respectively.
The conditions that we will impose: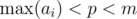 
, 
.
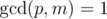Note. If you think about interpreting the expression, then we match the sequences {a0, a1, ..., an - 1} number of length n in the number in system with base p and take the remainder from its division by the number m, or the value of the polynomial (n - 1)-th power with coefficients ai at the point p modulo m. We'll talk about the choice of p and m later.
Note. If the value of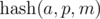 
(not by modulo), is placed in an integer data type (for example, a 64-bit type), then each sequence can be associated with this number. Then the comparison by greater / less / equal can be performed in O(1) time.
Comparison by equal in O(1) time
Now let's answer the question, how to compare arbitrary segments of sequence for O(1)? We show that to compare the segments of given sequence {a0, a1, ..., an - 1}, it is sufficient to compute the polynomial hash on each prefix of the original sequence.
Define a polynomial hash on the prefix as:
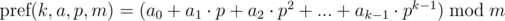
Briefly denote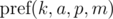 
as 
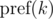and keep in mind that the final value is taken modulo m. Then:
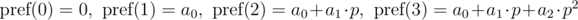
General form:
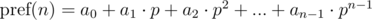
The polynomial hash on each prefix can be calculated in O(n) time, using recurrence relations:
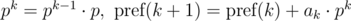
Let's say we need to compare two substrings that begin with i and j and have the length len, for equality:
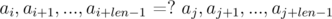
Consider the differences 
and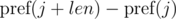 
. It's not difficult to see that:
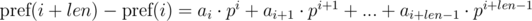
We multiply the first equation by pj, and the second by pi. We get:
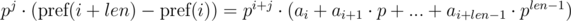
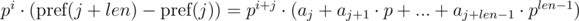
We see that on the right-hand side of the expressions in brackets polynomial hashes were obtained from the segments of sequence:
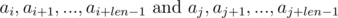
Thus, in order to determine whether the required segments of sequence have coincided, we need to check the following equality:
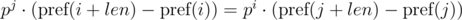
One such comparison can be performed in O(1) time, assuming the degree of p modulo precalculated. With the module m, we have:
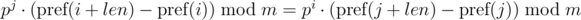
Problem: Comparing one segment of sequence depends on the parameters of the other segment of sequence (from j).
The first solution of this problem (given by veschii_nevstrui) is based on multiplying the first equation by p - i, and the second by p - j. Then we get:
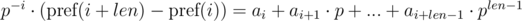
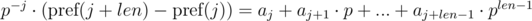
We can see that in the right-hand parts of equations we get a polynomial hash from the needed segments of sequence. Then, the equality is checked as:
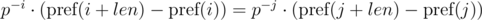
To implement this, we need to find the inverse element for p modulo m. From the condition gcd(p, m) = 1, the inverse element always exists. To do this, we need calculate or just know the value of the Euler function for the selected module φ (m) and get power φ(m) - 1 for p. If we precalculate the powers of the inverse element for the selected module, then the comparison can be performed in O(1) time.
The second solution we can use if we know the maximum lengths of compared segments of sequences. Let's denote the maximum length of compared lines as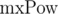 
. We multiply 1-th equation by power mxPow - i - len + 1 of p, and 2-nd equation by mxPow - j - len + 1 power of p. We get:
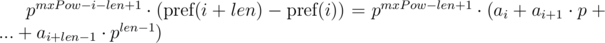
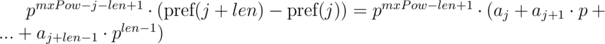
We can note that on the right-hand sides of equals a polynomial hash of segments of sequence. Then, the equality is checked as follows:
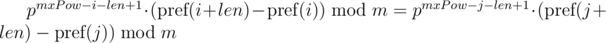
This approach allows you to compare one substring of length len with all substrings of length len by equality, including substrings of another string, since the expression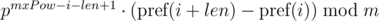 
for the substring of the length len starting at the position i, depends only on the parameters of the current substring i, len and constant mxPow, and not from the parameters of another substring.
Comparison by greater / less in O(log(n)) time
Consider two substrings of (possibly) different strings of lengths len1 and len2, (len1 ≤ len2), starting in the positions i and j respectively. Note that the ratio greater / less is determined by the first non-equal symbol in these substrings, and before this position strings are equal. Thus, we need to find the position of the first non-equal symbol by the binary search method, and then compare the found symbols. By comparing substrings to equality in O(1) time, we can solve the problem of comparing substrings by greater / less in O(log(len1)) time:
Minimizing the probability of collision
Using approximations in birthday problem, we get (perhaps a rough) estimate of the probability of collision. Suppose we compute a polynomial hash modulo m and, during the program, we need to compare n strings. Then the probability that the collision will occur:
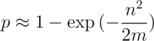
Hence it is obvious that m needs to be taken much more than n2. Then, approximating the exponential as Taylor series, we get the probability of collision on one test:
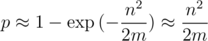
If we look at the problem of searching of occurrences of all cyclic shifts of one row in another string of lengths to 105, then we can get 1015 comparisons of strings.
If we take a prime modulo of the order 109, then we will not go through any of the maximum tests.
If we take a module of the order 1018, then the probability of collision on one test is ≈ 0.001. If the maximum tests are 100, the probability of collision in one of the tests is ≈ 0.1, that is 10%.
If we take the module of the order 1027, then on the 100 maximum tests the probability of collision is ≈ 10 - 10.
Conclusion: the higher the value of module, the more likely that we must pass the test. This probability not includes estimate probability of hack your solution.
Double polynomial hash
Of course, in real programs we can not take modules of the order 1027. How to be? To the aid comes the Chinese theorem on the remainders. If we take two mutually simple modules m1 and m2, then the ring of residues modulo m = m1·m2 is equivalent to the product of rings modulo m1 and m2, i.e. there is biection between them, based on the idempotents of the residue ring modulo m. In other words, if you calculate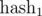 
modulo m1 and 
modulo m2, and then compare two segments of sequence with and simultaneously, then this is equivalent to comparing a polynomial hash modulo m. Similarly, we can take three mutually prime modules m1, m2, m3.
Features of the implementation
So, we came to the implementation of the above. Goal — the minimum of the number of the remainder calculation from the integer division, i.e. get two multiplications in a 64-bit type and one take the remainder from division in 64-bit type for one calculation of a double polynomial hash, get a hash modulo about 10^27 and protect the code from hacking on сodeforces
Selection of modules. It is advantageous to use a double polynomial hash on the modules m1 = 1000000123 and m2 = 2^64. If you do not like this choice of m1, you can select 1000000321 or 2^31-1, the main thing is to choose such a prime number so that the difference of the two residues lies within the signed 32-bit type (int). A prime number is more convenient, since the conditions gcd(m1, m2) = 1 andgcd(m1, p) = 1 are automatically provided. The choice of m2 = 2^64 is not accidental. The C++ standard ensures that all calculations in the unsigned long long are executed modulo 2^64 automatically. Separately, the module 2^64 can not be taken, because there is an anti-hash test, which does not depend on the choice of the hash pointp. The module m1 should be specified as constant to speed up the taking the remainder (the compiler (not MinGW) optimizes, replacing by multiplication and bitwise shifting).
Sequence encoding. If given a sequence of characters, consisting, for example, of small Latin letters, then you not need to encode anything, because each character already corresponds to its code. If a sequence of integers is given that is reasonable for a representation in memory of length, then it is possible to collect all the occurring numbers into one array, sort, delete the repeats and assign to each number in the sequence its index in sorted set. Code zero is forbidden: all sequences of the form 0,0,0, .., 0 of different length will have the same polynomial hash.
Choosing of the base. As the base p it suffices to take any odd number satisfying the condition max(a[i]) < p < m1. (odd, because then gcd(p, 2 ^ 64) = 1). If you can be hacked, then it is necessary to generate p randomly with every new program start, and generation with std::srand(std::time(0)) and std::rand() is a bad idea, because std::time(0) ticks very slowly, and std::rand() does not provide enough uniformity. If the compiler is not MINGW (unfortunately, MinGW is installed on the codeforces), then you can use std::random_device, std::mt19937, std::uniform_int_distribution<int> (in cygwin on windows and gnu gcc on linux this set provides almost absolute randomness). If you were unlucky and you use only MinGW, then there is nothing left to do but replace std::random_device with std::chrono::high_resolution_clock and hope for the best (or is there a way to get some counter from the processor?). On MinGW, this timer ticks in microseconds, on cygwin and gnu gcc in nanoseconds.
Warranties against hacking. Odd numbers up to a module of the order of 10^9 are also of the order of 10^9. The cracker will need to generate an anti-hash test for each odd number so that there is a collision in the space to 10^27, compile all the tests into one big test and hack you! This is if you do not use MinGW on Windows. On MinGW, the timer is ticking, as already mentioned, in microseconds. Knowing when solution was started on the server with an accuracy of seconds, it is possible for each of the 10^6 microseconds to calculate what random p was generated, and then the number of variants in the 1000 times less. If 10^9 is some cosmic number, then 10^6 already seems not so safe. If you use std::time (0) only 10^3 number of variants (milliseconds) — can be hacked! In the comments I saw that grandmasters know how to break a polynomial hash modulo ot order of 10^36.
Ease of use. It is convenient to write a universal object for a polynomial hash and copy it to the task where it might be needed. It is better to write independently for your needs and goals in the style in which you write to understand the source code if necessary. All problems in this post are solved by copying the one class object. It is possible that there are specific tasks in which this does not work.
Problem 1. Searching all occurrences of one string of length n in another string length m in O(n + m) time
Problem 2. Searching for the largest common substring of two strings of lengths n and m (n ≥ m) in O((n + m·log(n))·log(m)) time
Link on problem on acm.timus.ru.
Problem 3. Finding the lexicographically minimal cyclic shift of a string of length n in O(n·log(n)) time
Problem 4. Sorting of all cyclic shifts of a string of length n in lexicographic order in O(n·log(n)2) time
Problem 5. Finding the number of sub-palindromes of a string of length n in O(n·log(n)) time
Link on problem 5 with length 10^5
Link on problem 5 with length 10^6
Problem 6. The number of substrings of string of length n that are cyclic shifts of the another string length m in O((n + m)·log(n)) time
Problem 7. The number of suffixes of a string of length n, the infinite extension of which coincides with the infinite extension of the given string for O(n·log(n)) (extension is a duplicate string an infinite number of times).
Problem 8. Largest common prefix of two strings length n with swapping two chars in one of them in O(n·log(n)) time
You can check the editorial written by a_kk and smokescreen on this site for getting solution without hashes in O(n) time.
That's all. I hope this post will help you to apply hashing and solve more difficult problems. I will be glad to any comments, corrections and suggestions from you. Share other problem and, possibly, your solutions, solutions without hashes. Thank you for reading this tutorial! There are many useful comments in russian under this blogpost, if you want, you can check them with google translate.
Links:
