Hello Codeforces. Today I'm writing about a Math topic that is simple, but resources and problems are very limited on Programming Contest Websites.

SLAE stands for system of linear equations. Basically, consider we have a set of equations of the form :

a₀·x₀ + a₁·x₁ + a₂·x₂ + ... + a_n - 1·x_n = m

b₀·x₀ + b₁·x₁ + b₂·x₂ + .... + b_n - 1·x_n - 1 = n

c₀·x₀ + c₁·x₁ + c₂·x₂ + .... + c_n - 1·x_n - 1 = o

.....

Note that all a, b, c... are real-valued arrays and all m, n, o are arbitrary reals. Realize how x₀, x₁, ...x_n - 1 appear in each of the equations.

Now, we want to find values of [x₀, x₁...x_n - 1] that satisfy each of the given equations listed. The simplest method to find such solutions is to use Gaussian Elimination, that solves the problem in O(N³), where N = number of equations = number of variables .

To Learn about Gaussian Elimination, click here. Today, we shall learn about 2 special class of problems that can be solved using Gaussian Elimination for SLAE.

Problem 1 : Markov Chains and Cyclic Expected Values :

Many a times as a part of expected value problems, you are expected to sum up infinite series that hold as limits, as probabilities lie in the closed interval [0, 1]. For example,

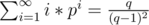, as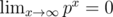

However, not always can we expect to reach such simple sums. Consider the following example :

You are given Tree T consisting of N nodes. Initially there is a player in node S. In a single move, he moves to one of the adjacent nodes of the node he is currently at, each with equal probability. What is the expected number of moves before he reaches node T ?.

Here, we need to understand that the probabilities are infinite as well as cyclic. Creating a simple formula for the answer is quite hard. However, notice that we can create a transition matrix, as the procedure conducted on the tree is a markov chain.

Create a matrix P, where P[i][j]= probability of moving from node i to j in a single move. Now, Let E(i) denote the expected number of steps needed to reach node T from node i.

.

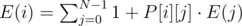Try and take a moment and think about why this formula is correct.

Surprise Surprise, this can be modeled as SLAE. Rewrite equations as :

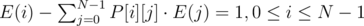. So the system is :

\begin{equation} \begin{pmatrix} 1-P[0][0] & -P[0][1] & ... & -P[0][N-1] \newline -P[1][0] & 1-P[1][1] & ... & -P[1][N-1] \newline .... \newline -P[N-1][0] & -P[N-1][1] & ... & 1-P[N-1][N-1] \end{pmatrix} \cdot \begin{pmatrix} E(0) \newline E(1) \newline . \newline . \newline E(n-1) \end{pmatrix} = \begin{pmatrix} 1 \newline 1 \newline .. \newline 1 \end{pmatrix} \end{equation}

This is the equation I_N - P = 1. Note that for node T, we need to have P[t][i] = 0, t ≠ i and P[t][t] = 1, as we won't move from node T, it is an absorbent state of the markov chain. So, the T^th row of matrix I_N - P will be all zeros. Just remove it from both sides of the equation. Now, we know that unique expected values exist. (Obviously, they exist, that is the problem given). So, just invert the matrix , to get the expected values.