You are given the first n (or n + 1 if necessary) terms of a former power series P(x) = c₀ + c₁x + c₂x² + .... What operations can be performed efficiently?

• Obviously, P(x) + Q(x), P(x) - Q(x), P'(x), 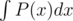, kP(x) for a given constant k, can be done in O(n).

• P(x)Q(x) can be done in O(nlogn) by FFT.

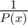• can be done in O(nlogn): Link, check problem E

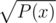• can be done in O(nlogn): Link, check problem E

• exp(P(x)) can be done in O(nlogn): Link, check Figure 1, left

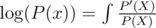• : Link

• Open: Can we do more complicated operations like P(Q(x)), P(x)^1 / k, sin(P(x)), arcsin(P(x)), etc.? Are there other important operations?

• Probably a bit related to the computation of 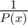: when we are given two big decimal number x and y, can we compute x / y?